Pandas / 딥러닝 학습방법 이해하기

판다스 / 역전파 알고리즘

판다스는 구조화된 데이터의 처리를 지원하는 Python 라이브러리입니다.
고성능 array 계산 라이브러리인 numpy와 통합하여, 강력한 “스프레드시트” 처리 기능을 제공하므로 Data science 분야애서 널리 쓰이는 판다스를 알아봅니다.

---

기계학습 문제 대부분은 학습 단계에서 최적의 매개변수를 찾아야 합니다. 최적의 매개변수란 손실 함수가 최솟값이 될 때의 매개변수 값 입니다.

그런데 딥러닝에서는 여러 뉴런들이 여러 층을 형성하여 구성이 될 수 있고, 끝 출력층의 매개변수 뿐만 아니고 뒤의 각 층에 할당된 매개변수가 업데이트 되어야 올바른 학습이 될 수 있는데, 이 각각의 매개변수들을 학습시키는 것이 역전파법 이라고 할 수 있습니다.

판다스

구조화된 데이터의 처리를 지원하는 Python 라이브러리로서 고성능 array 계산 라이브러리인 numpy와 통합하여, 강력한 “스프레드시트” 처리 기능을 제공합니다.

데이터를 잘라서 볼 수 있는 인덱싱, 각종 연산에 필요한 함수, 데이터를 알맞게 다듬을 수 있는 전처리 함수 등을 제공하고 있습니다.

주로, 데이터 처리 및 통계 분석을 위해 사용되고 있습니다.

판다스 설치

1. conda에서 가상환경을 생성하고, 그 환경 안에 판다스를 설치합니다.
2. jupyter notebook에서 작업하기 위해 jupyter notebook이라고 입력합니다.

conda create -n ml python=3.8 # 가상환경생성
activate ml # 가상환경실행
conda install pandas # pandas 설치

jupyter notebook # 주피터 실행하기

데이터 로딩

밑의 그림에서 볼 수 있듯이, 판다스를 임포트하고 데이터가 있는 주소를 가져와 판다스의 csv를 읽는 객체에 연결시켜준 모습을 볼 수 있습니다.

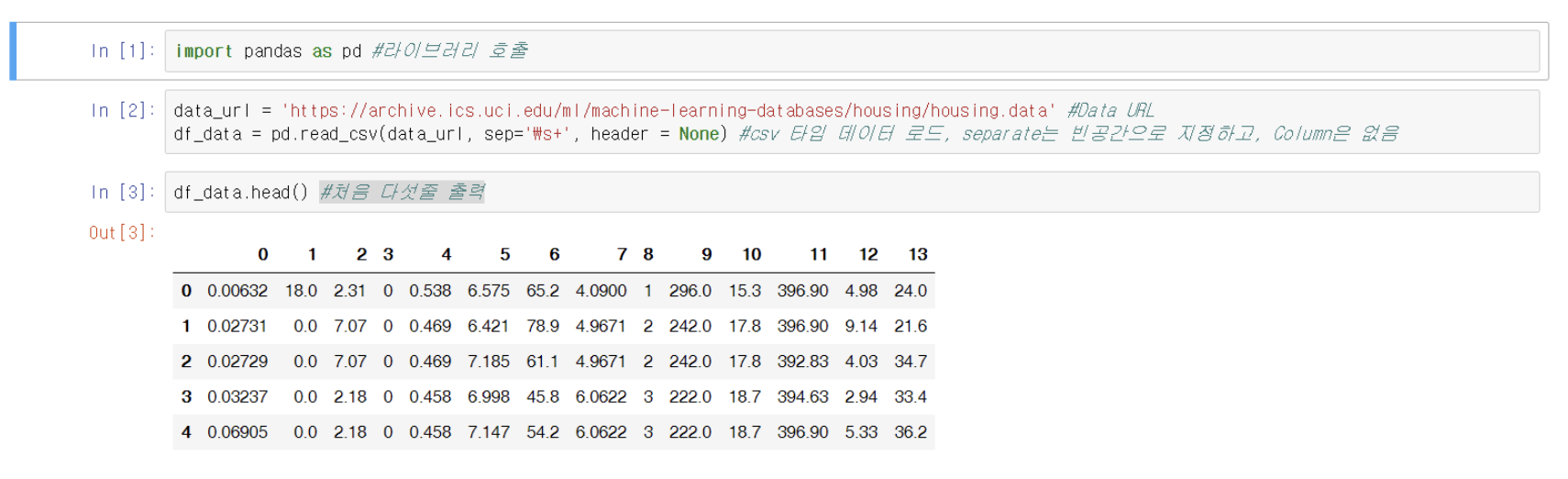
pandas의 구성

판다스의 데이터셋은 크게 두가지인 시리즈 객체와 데이터프레임 객체로 볼 수 있습니다.

• Series : DataFrame 중 하나의 Column에 해당하는 데이터의 모음 Object, column vector를 표현하는 object
• DataFrame : DataTable 전체를 포함하는 Object, Series를 모아서 만든 Data Table = 기본 2차원

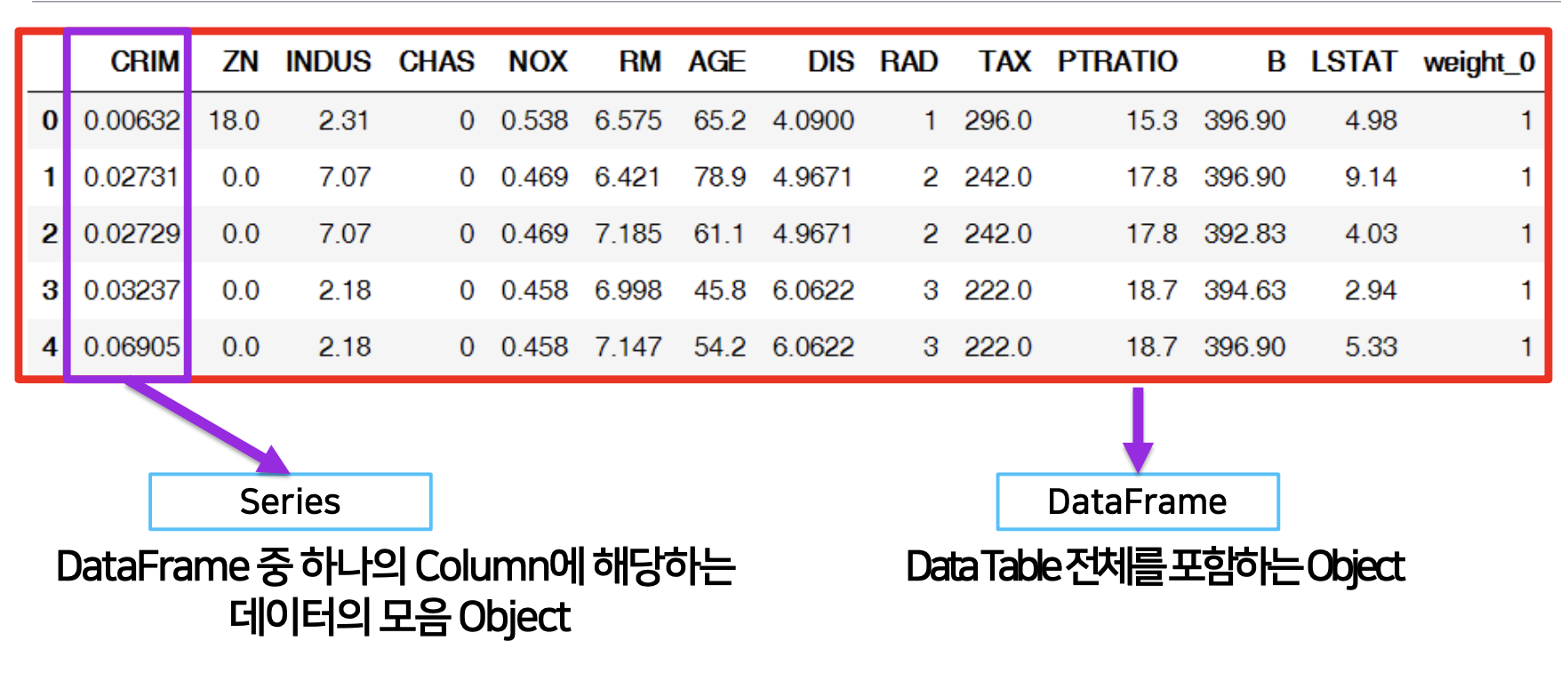
dataframe indexing

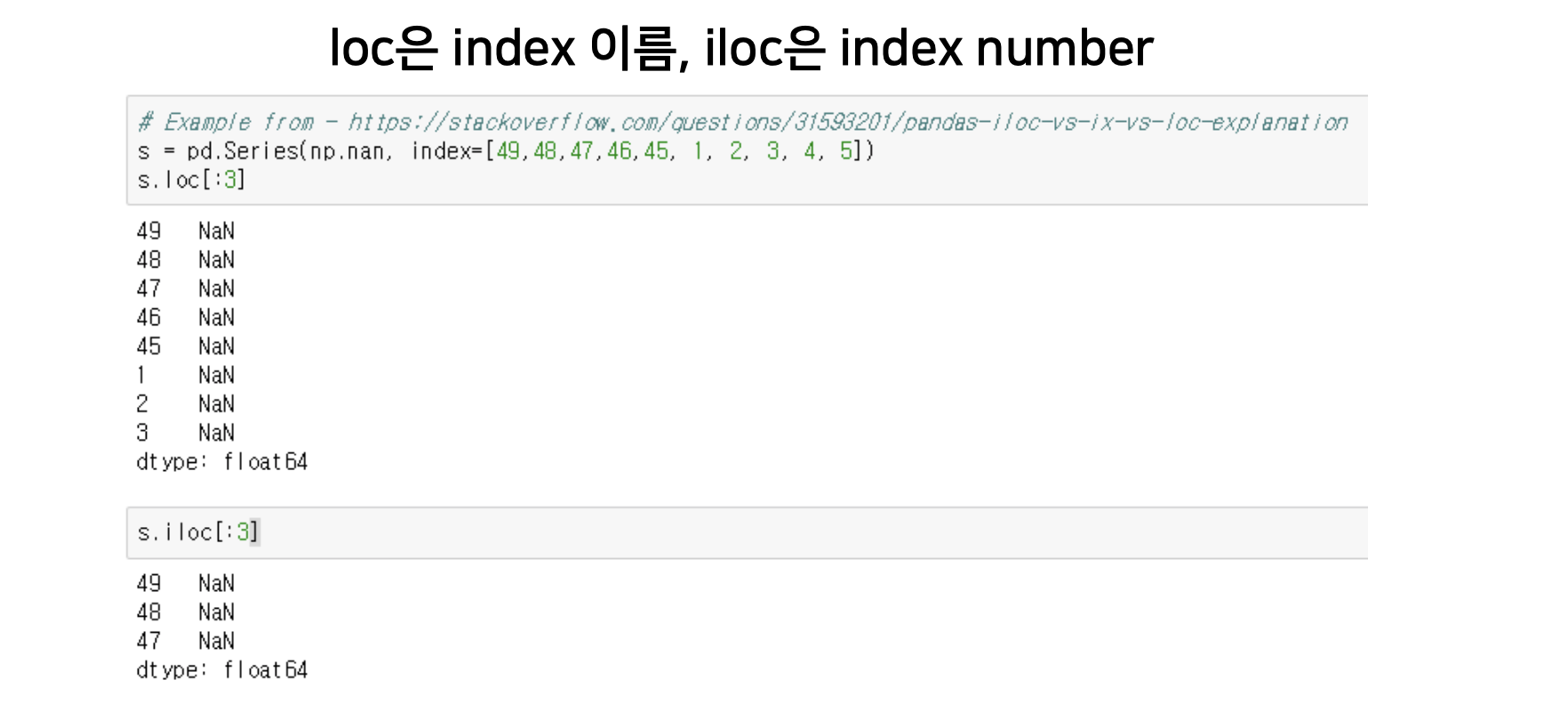
데이터 프레임에서 인덱스를 이용하여 자유자제로 데이터를 인덱싱 해볼 수 있습니다.

• loc : 행의 인덱스 값 자체(이름)를 이용해 인덱싱을 수행합니다.
• iloc – 행의 인덱스(위에서 부터 순서대로 0, 1, 2…)를 이용해 인덱싱을 수행합니다.

Selection with column names

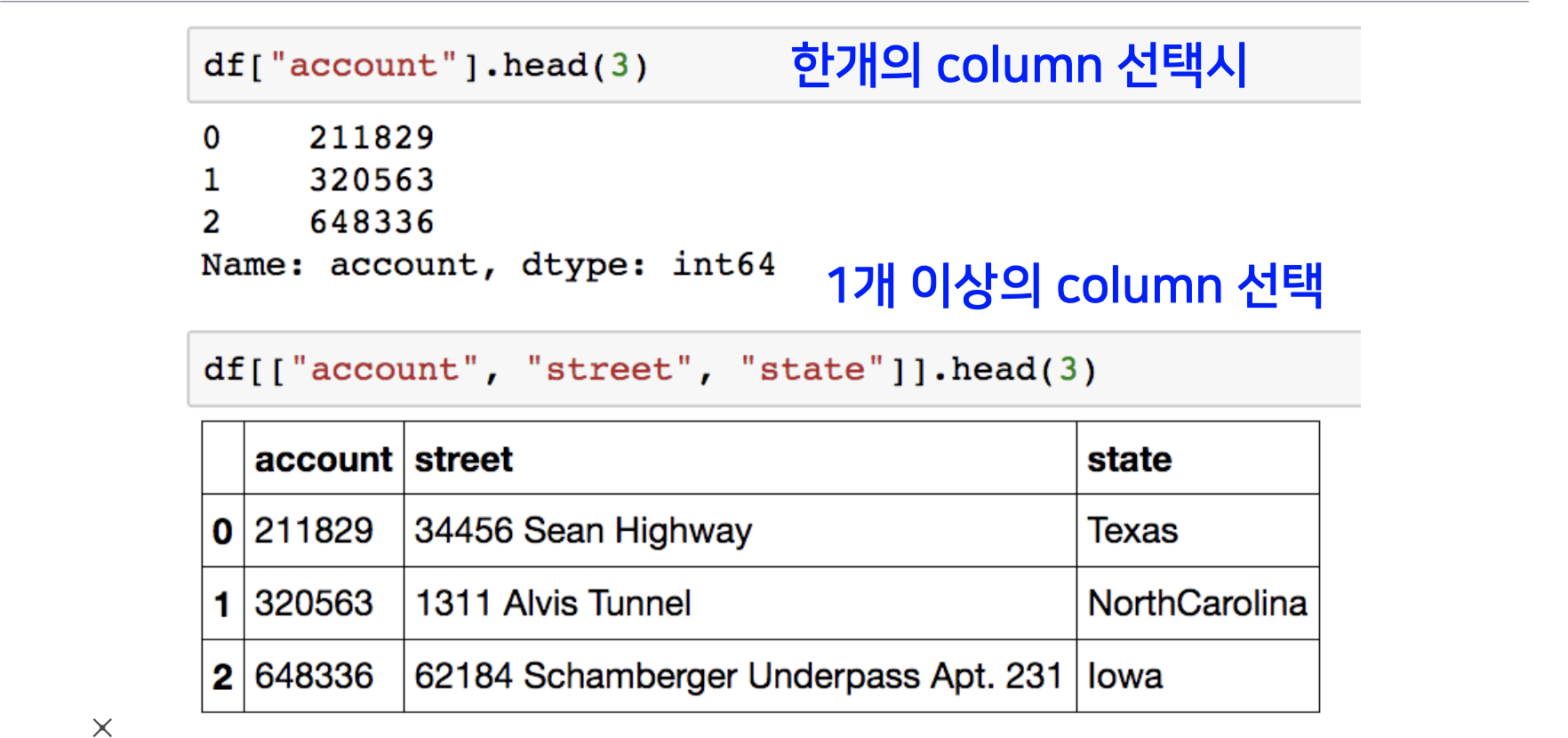
데이터 프레임 객체에서 여러 칼럼이 있을거지만, 특정 칼럼 네임만 특정해서 데이터를 모아 볼 수 있습니다.

형식은 DataFrame_name['col_name'] or DataFrame_name[['col_name1', 'col_name2',]] 입니다.

특정 한개의 칼럼네임으로만 지정한다면 시리즈 객체로 데이터가 반환이 되고, 여러개는 데이터 프레임 객체로 반환이 됩니다.

df["account"][:3] 처럼, column 이름과 함께 row index 사용 시 몇번 째 데이터 까지만 가져올지 정할 수 있습니다.

data drop

데이터 프레임 객체에서 행의 데이터를 삭제하는 방법은 drop이라는 빌트인 함수를 씀으로 수행이 가능합니다.

하나의 행만 삭제하고자 할 때는 삭제하고자 하는 행의 인덱스 넘버를, 한 개 이상의 행을 삭제하고자 할 때는 리스트 형식으로 인덱스 넘버를 drop 함수 arguement에 넣어주면 됩니다.

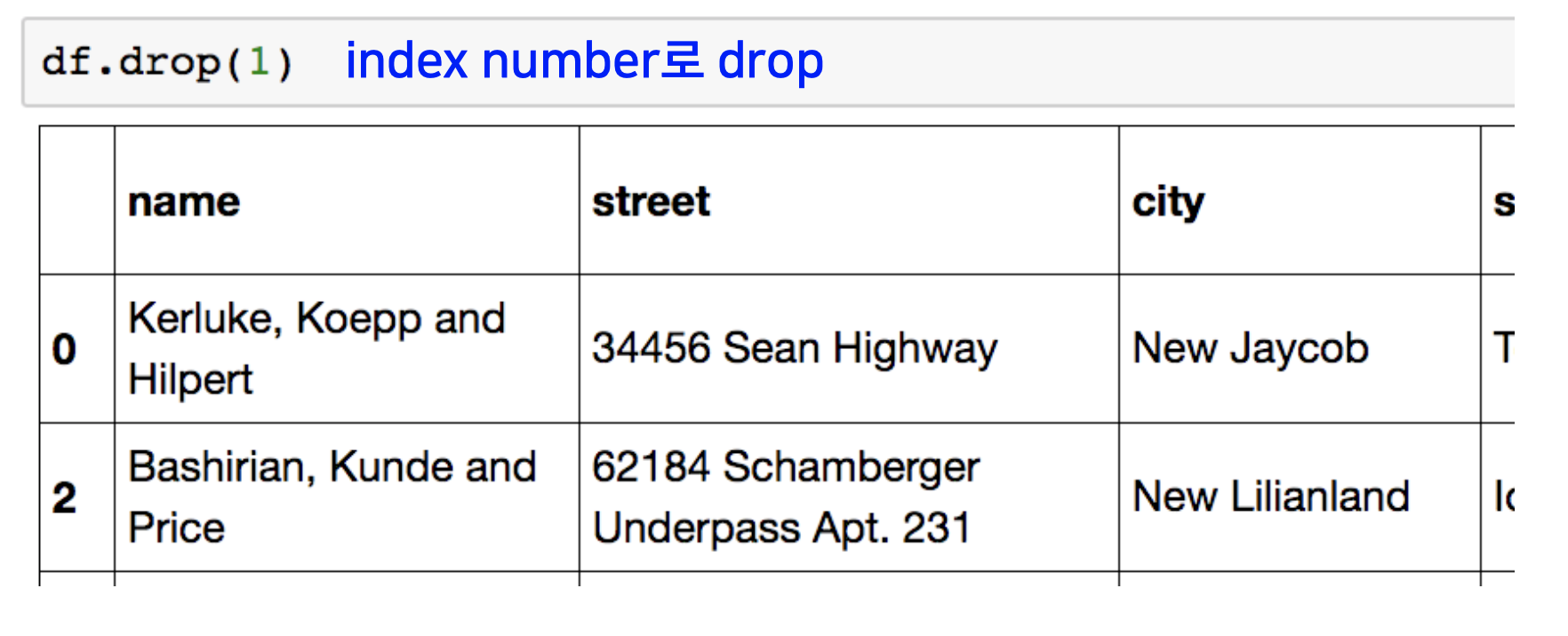
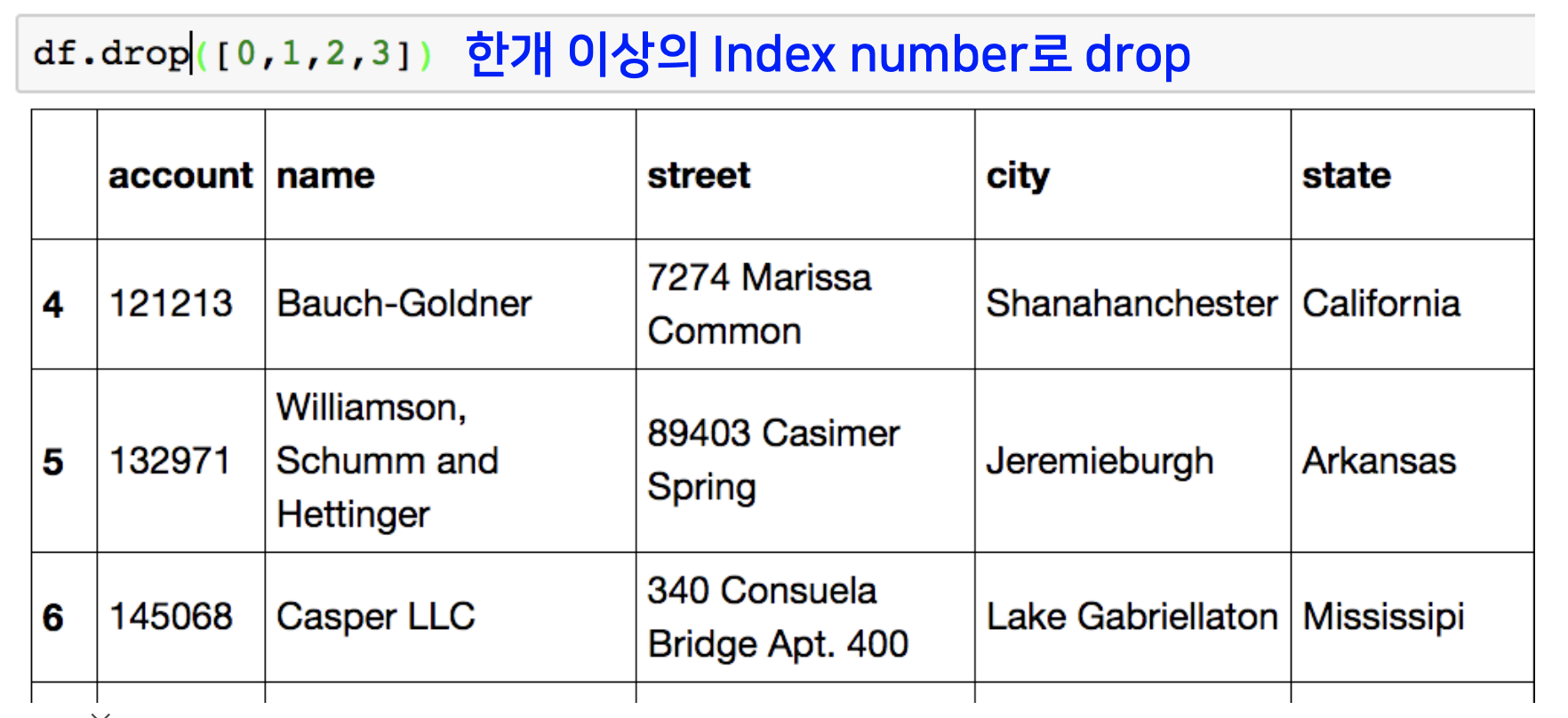
또는 칼럼 네임을 지정해 주어 칼럼 전체를 삭제할 수도 있습니다.

dataframe operation

판다스는 시리즈 객체끼리 또는 시리즈와 데이터 프레임 객체 끼리의 더하고 빼고 나누는 등의 연산을 지원합니다.

• Operation types: add, sub, div, mul

시리즈와 시리즈끼리는 인덱스를 기준으로 연산을 수행합니다.
이 때, 겹치는 인덱스가 없을 경우는 NaN값을 반환합니다.

데이터 프레임 객체 끼리는 column과 index를 모두 고려합니다.
서로 column과 index 겹치는 구간이 없을 때는 NaN으로 채워지게 됩니다.
fill_value를 씀으로써 NaN을 특정 값으로 매핑할 수도 있습니다.

pandas map

pandas의 series type의 데이터에도 map 함수가 사용이 가능합니다.

통상 map의 기능은 어떤 값을 받아서 map 안에서 정의된 함수나 여러 프로시저에 의해 그 값이 변화되어 반환되게 하는 함수를 의미합니다. 이를 전체 데이터에 대해 수행합니다.

예제는 0-9까지의 값을 가지는 시리즈 객체를 만들고, 앞에서 부터 5개를 조회하는 연산입니다.
그 다음, map 함수에 익명 함수 람다를 넣어 각 시리즈 객체의 값 들을 전부 제곱하게 됩니다.

map 함수에 function 대신 대신 dict, sequence형 자료등으로 대체 가능합니다.

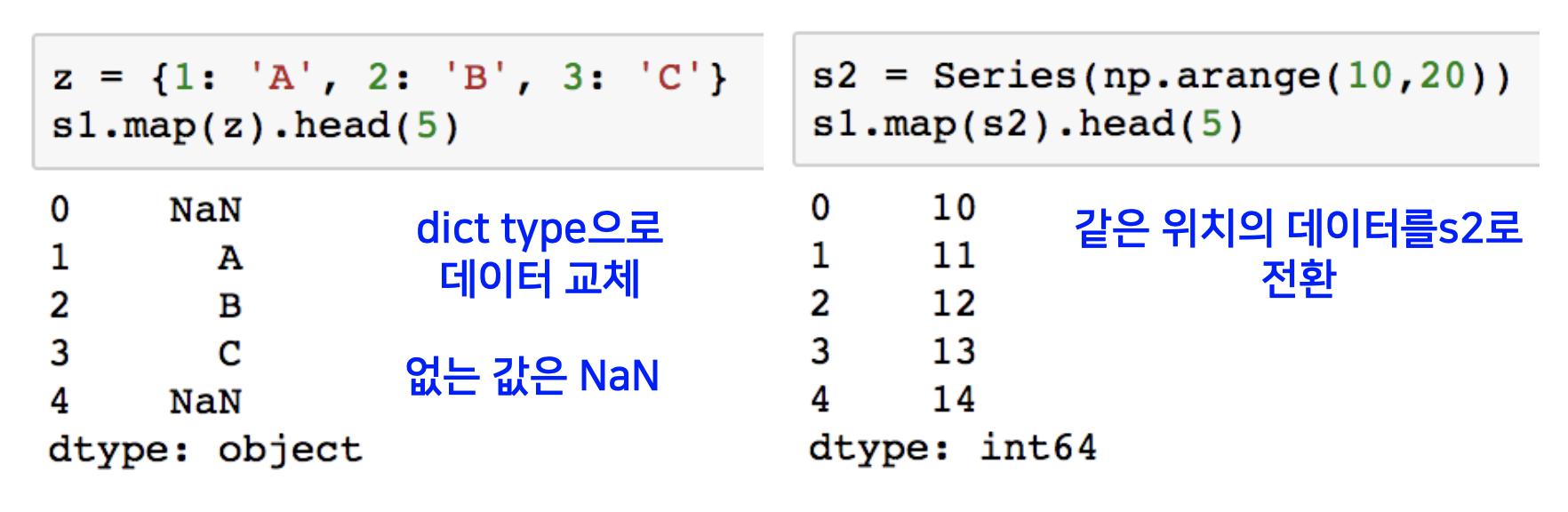
역전파 알고리즘

기계학습 문제 대부분은 학습 단계에서 최적의 매개변수를 찾아야 합니다. 최적의 매개변수란 손실 함수가 최솟값이 될 때의 매개변수 값 입니다.

그런데 딥러닝에서는 여러 뉴런들이 여러 층을 형성하여 구성이 될 수 있고, 끝 출력층의 매개변수 뿐만 아니고 뒤의 각 층에 할당된 매개변수가 업데이트 되어야 올바른 학습이 될 수 있는데, 이 각각의 매개변수들을 학습시키는 것이 역전파법 이라고 할 수 있습니다.

신경망을 수식으로 분해해보기

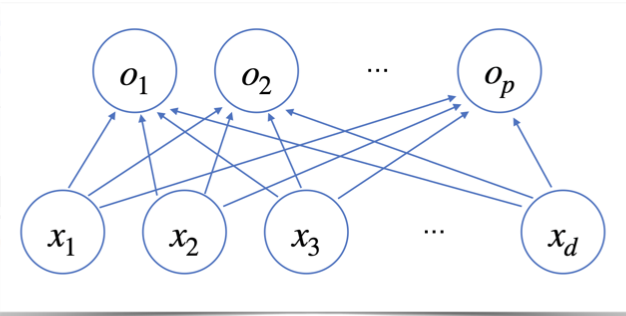
위의 그림과 같은 신경망 모델은 다음과 같은 백터와 행렬들의 조합으로 표현될 수 있습니다.

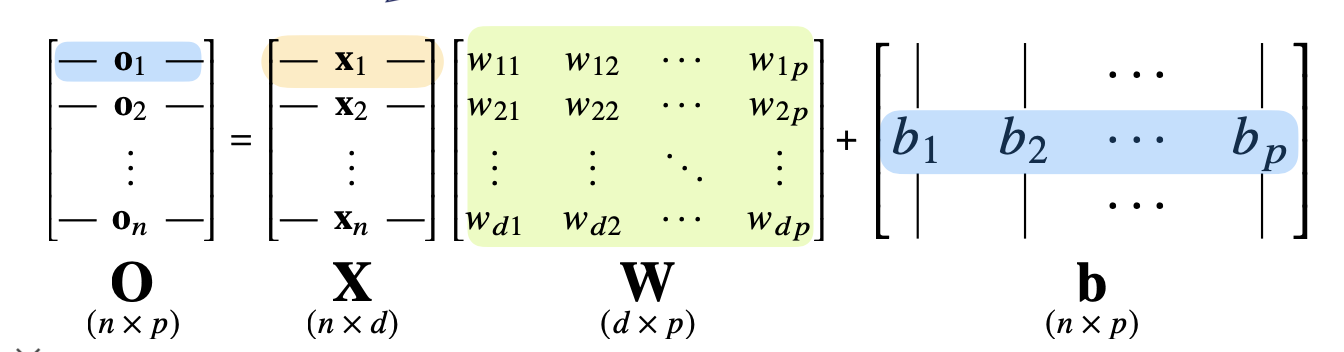
O 행렬은 해당 층에서의 출력 값을 의미하게 됩니다.
이는 행렬 X와 학습 매개변수 W의 내적 값 그리고 바이어스 텀을 더함으로써 계산이 되게 됩니다.

각 행벡터 oi 는 데이터 xi 와 가중치 행렬 W 사이의 행렬곱과 절편 b 벡터의 합으로 표현이 됩니다.

oi = xi (행렬곱) W + bias vector

oi 백터의 값의 계산을 풀어쓰면 다음과 같습니다.

o1 벡터의 첫 번째 값의 계산은 먼저 x1벡터와 w11 ~ wd1까지의 벡터의 내적 값 + b1로 계산이 됩니다.

o1 벡터의 두 번째 값의 계산은 x1벡터와 w12 ~ wd2까지의 벡터의 내적 값 + b2로 계산이 됩니다.

나머지 데이터에 대해서도 이와 마찬가지로 계산이 수행됩니다.

데이터가 바뀌면 결과값도 바뀌게 됩니다. 이 때 출력 벡터의 차원은 d 에서 p 로 바뀌게 됩니다.

소프트맥스 연산

소프트맥스(softmax) 함수는 모델의 출력을 확률로 해석할 수 있게 변환해 주는 연산입니다 분류 문제를 풀 때 선형모델과 소프트맥스 함수를 결합하여 예측합니다.

이와 같이 출력 값(벡터, 행렬)에 비선형 함수인 소프트맥스라는 함수를 통과시켜주게 되면 확률 백터가 되고 이는 특정 클래스 k에 속할 확률로 해석할 수 있습니다.

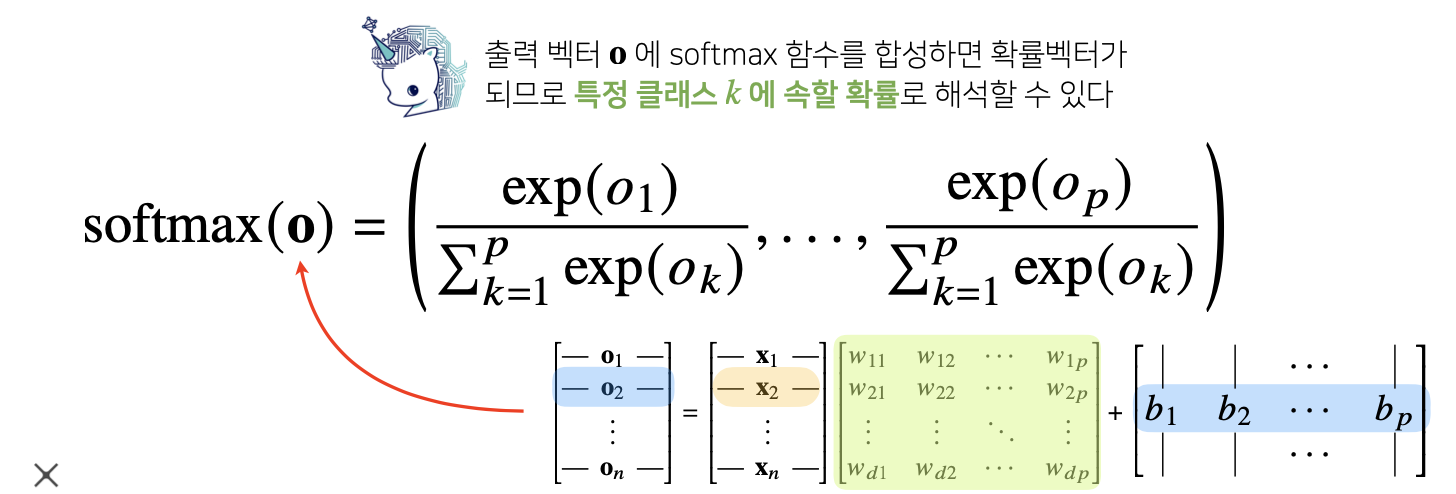
신경망은 선형모델과 활성함수를 합성한 함수

앞서 데이터와 매개변수 행렬을 행렬곱을 하고 그리고 바이어스 텀을 더하여 복잡한 선형모델을 만들었습니다.
신경망은 선형모델에서 나온 출력 값을 비선형 활성 함수와 합성해 만든 또 다른 함수를 말합니다.

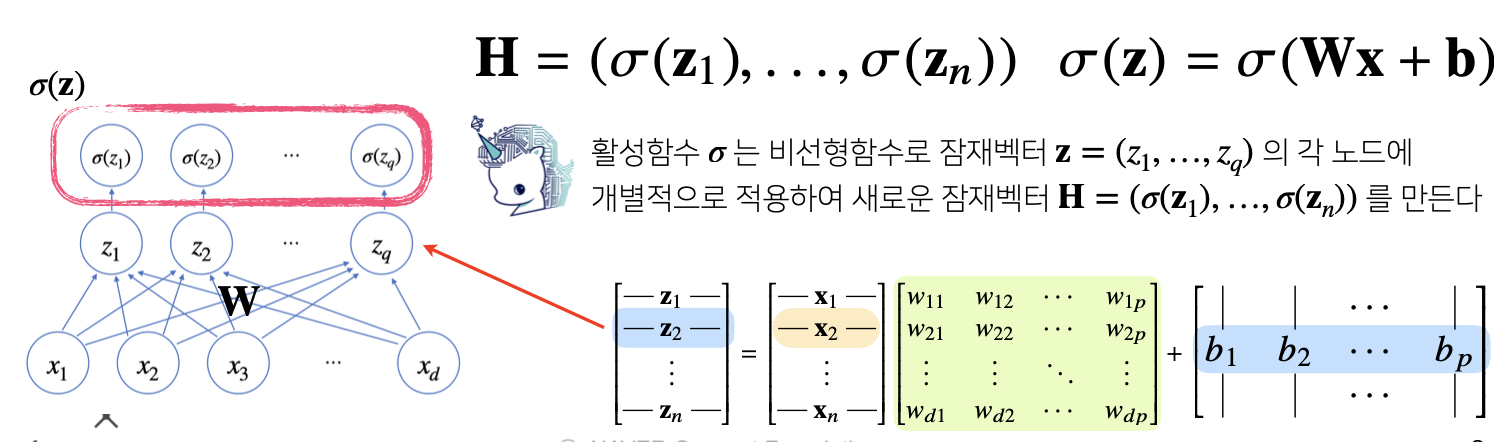
활성함수란

활성함수(activation function)는 비선형(nonlinear) 함수 로서 딥러닝에서 매우 중요한 개념입니다.
활성함수는 선형모형의 출력을 비선형하게 변환해주는 역할을 합니다.
시그모이도(sigmoid) 함수나 tanh 함수는 전통적으로 많이 쓰이던 활성함수 지만 딥러닝에선 ReLU 함수를 많이 쓰고 있습니다.

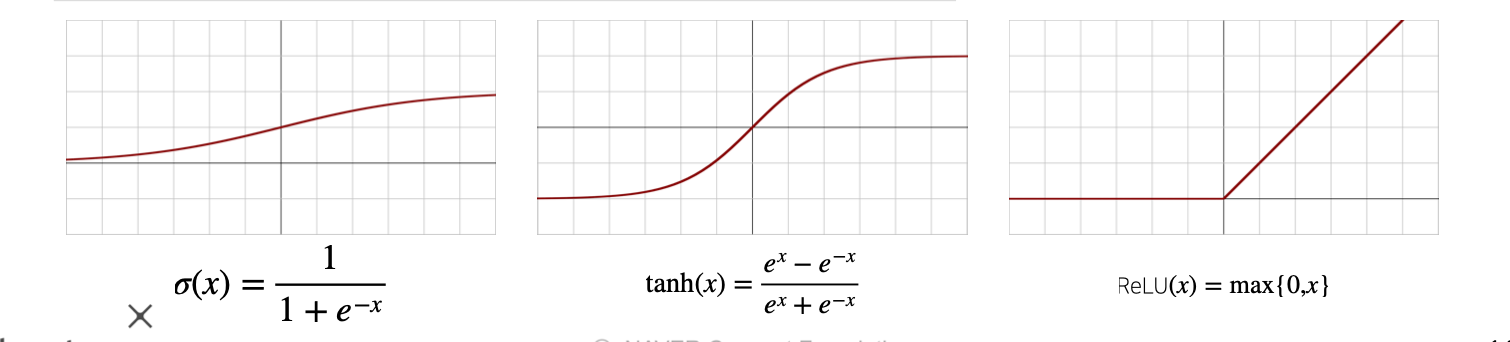
다층 신경망

앞서 살펴본 신경망을 여러개 층으로 쌓은 것이 다층 신경망입니다.

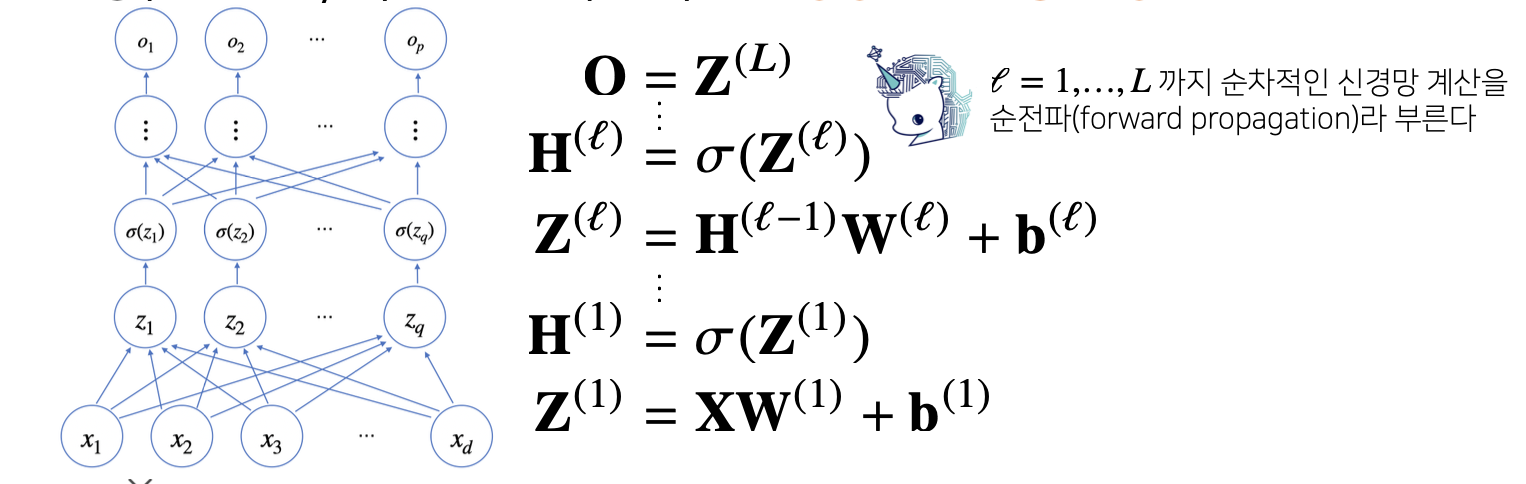
처음 계산된 Z(1)의 값이 활성함수를 통과해 H(1)이 되면 여기까지 한 층의 계산 입니다.
다시 H(1)이 다른 층으로에 입력 값으로 들어가 W(2)와 행렬곱이 되고 바이어스 텀이 더해져 Z(2)가 되고, Z(2)가 활성함수 층을 통과하면 H(2)가 됩니다.
이 출력 값을 계산 다음 층으로의 입력으로 넣어 계산을 수행하게 되고, 이를 다층 신경망이라고 합니다.

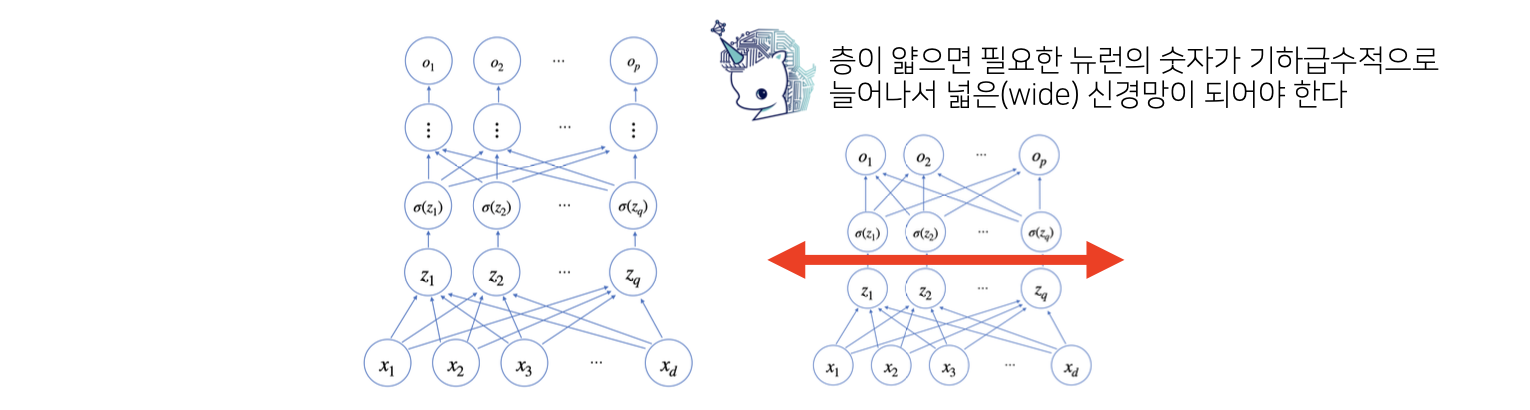
왜 층을 여러개를 쌓나요?

이론적으로는 2층 신경망으로도 임의의 연속함수를 근사할 수 있습니다.
그러나 층이 깊을수록 목적함수를 근사하는데 필요한 뉴런(노드)의 숫자가 훨씬 빨리 줄어들어 좀 더 효율적으로 학습이 가능합니다

딥러닝 학습원리: 역전파 알고리즘

신경망이 여러 층으로 쌓이게 되고, 각층에 있는 학습 패러메터 각각에 학습이 이루어 지기 위해 이 역전파 알고리즘을 사용할 수 있습니다.

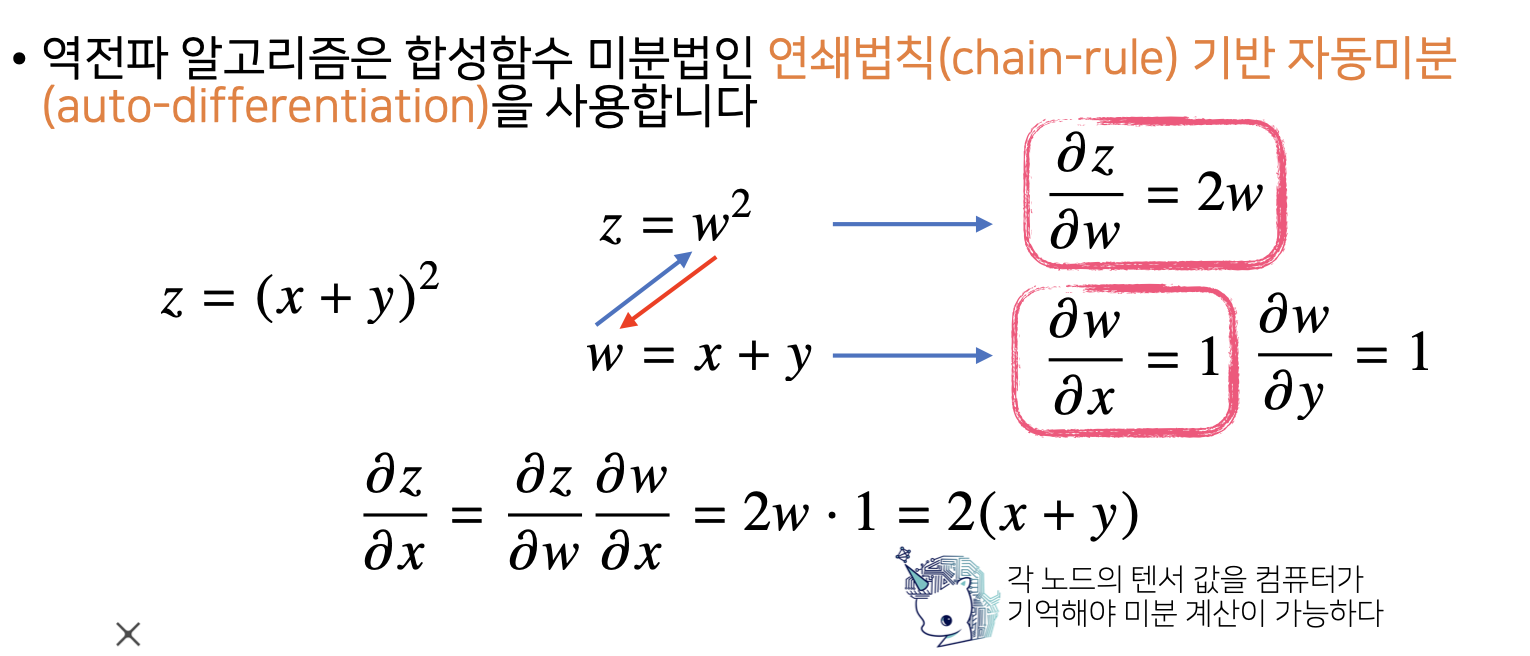
역전파 알고리즘은 합성함수 미분법인 연쇄법칙(chain-rule)기반 자동미분(auto-differentiation)을 사용합니다.

경사 하강법에서 우리는 각 변수에서의 그레디언트 값을 계산하였습니다. 그레디언트 값(기울기=미분 값)은 이 변수값이 어디로 가야 우리의 목적함수를 최저값으로 만들 수 있는가를 알려주는 값이라고 할 수 있었습니다. 경사하강법에서는 변수 값에서 그레디언트 값을 빼줌으로서 우리의 목적함수를 최소화 할 수 있었습니다.

위의 그림에서도 마찬가지 입니다.
우리는 $z$ 값에 대해 $x$가 얼마만큼의 변화가 있는지 (미분 값 = 기울기)를 구하고 싶습니다.
하지만 위 함수는 합성합수 이기 때문에, 한번에는 안되고 한 단계를 더 거쳐야 구할 수 있습니다.

여기서 합성함수 미분법인 연쇄법칙을 사용하여 구할 수 있습니다.

$\frac{\partial z}{\partial x}$ 구하기

1. 먼저 겉미분을 합니다.
   $w$를 $(x+y)$라 놓고, $z$를 $w$에 대해서 편미분을 하면 $ \frac{\partial z}{\partial w} = 2w $가 됩니다.

2. 다음은 속미분을 합니다.
   $w$를 $(x+y)$라 놓았으니 $w$를 $x$대해서 편미분을 하면 $ \frac{\partial w}{\partial x} = 1$이 됩니다.

3. 그 다음 합성합수 연쇄법칙에 의해 $ \frac{\partial z}{\partial w} \frac{\partial w}{\partial x}$에서 ${\partial w}$텀이 약분되게 되고 결론은 $ \frac{\partial z}{\partial x}$가 도출되게 됩니다.

---

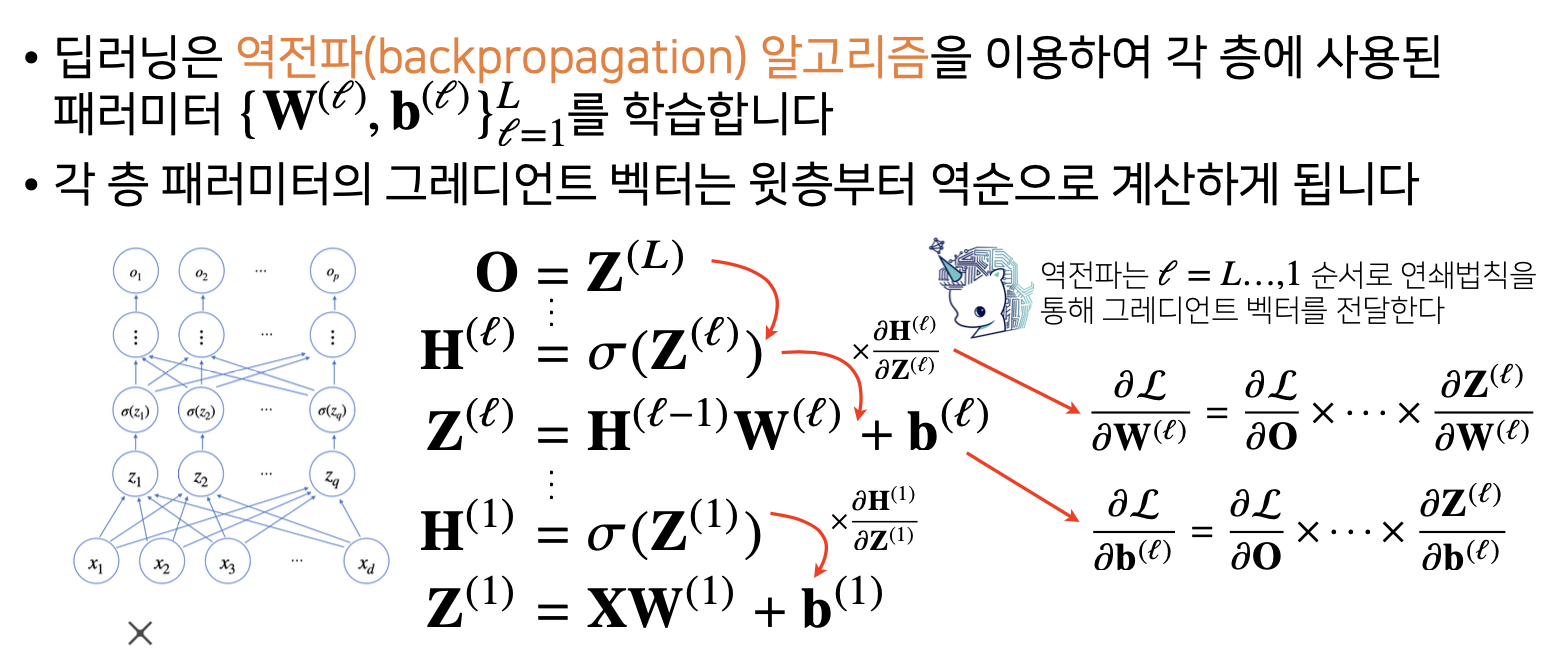
딥러닝에서도 위와 같은 아이디어가 똑같이 적용됩니다.

딥러닝은 역전파(backpropagation) 알고리즘을 이용하여 각 층에 사용된 패러미터 ${W(l), b(l)}1$에서$l1$ 까지를 학습합니다

각 층 패러미터의 그레디언트 벡터는 윗층부터 역순으로 계산하게 됩니다

위의 그림처럼 목적함수 $L$에 대한 $w(l)$의 그레디언트를 계산한다면 다음과 같이 계산해 볼 수 있습니다.

$\frac{\partial L}{\partial w^{(l)}} = \frac{\partial L}{\partial O} \bullet \bullet \bullet \frac{\partial H^{(l)}}{\partial Z^{(l)}} \frac{\partial Z^{(l)}}{\partial W^{(l)}}$

피어세션 정리

두 번째 주차 셋째날 모임이었습니다.

오늘의 further question은 분류 문제에서 softmax 함수가 사용되는 이유가 뭘까요? 와 softmax 함수의 결과값을 분류 모델의 학습에 어떤식으로 사용할 수 있을까요? 이었고, 이에 대해 열심히 서로 토의를 해보았습니다.

그리고 오늘 공부하였던 내용 중에 약간 이해가 안되는 부분(소프트맥스를 구현하는 넘파이 코드에 있어서 왜 최대값을 전체 백터에 대해 빼주고, 이것이 어떻게 동작하는지? 와 역전파가 어떻게 계산이 되는지)이 있는 분이 계서서 질문을 듣고, 다 같이 여러 방향으로 자기가 생각해 본 것을 공유해보는 시간을 가졌었습니다.

그리고 내일 있을 10개 조씩 묶어서 3분씩 조를 소개하는 시간에 사용될 프레젠테이션을 만들기 위해 서로 협동하여 논의하는 시간을 가졌었습니다.

퀴즈 정리

1. $ReLU(x) = max(0,x)$ 일 때, $ReLU(-3.14)$ 의 값을 구하시오

   $x$가 $0$보다 작다면 $0$을, $x$가$0$보다 크다면 $x$를 반환하게 되는 함수였습니다.

2. $\partial tanh(x) = \frac{\partial tanh(x)}{\partial x}$ 일 때, $\partial tanh(0)$의 값을 구하시오.

   $tanh(x)$를 미분하여 $x$에 $x$을 대입한 값을 구해주면 되는 문제였습니다.

3. 다음 보기 중 역전파 (backpropagation) 알고리즘의 기반이 되는 것을 고르시오.

   역전파 알고리즘의 핵심은 바로 합성함수의 연쇄법칙에 있습니다.

4. 다음 보기 중 신경망에서 활성함수가 필요한 가장 적절한 이유를 고르시오.

   선형모델의 출력을 비선형 적으로 근사하기 위하여 필요합니다.

5. $z$ 와 $k$ 가 다음과 같이 주어질 때, $\frac{\partial z}{\partial x}$값으로 올바른 것을 고르시오.

   $z = (k + 3)^{2}$ $k = (x + y)^{2}$

   $\frac{\partial z}{\partial x} = \frac{\partial z}{\partial k} \frac{\partial k}{\partial x}$ 가 됩니다.

   $\frac{\partial z}{\partial k}$은 $3(k+3)^{2}$
   $\frac{\partial k}{\partial x}$은 $2(x+y)$

   즉, $6((x+y)^{2}+3)^{2}(x+y)$가 됩니다.

References

• pandas - 최성철 교수님
• Mathematics for Artificial Intelligence - Unist 임성철 교수님