경사하강법 (Gradient Descent)

경사법

경사법은 최솟값을 찾나, 최댓값을 찾나에 따라 경사하강법과 경사상승법으로 나뉩니다.

기계학습 문제 대부분은 학습 단계에서 최적의 매개변수를 찾아야 합니다. 최적이란 손실 함수가 최솟값이 될 때의 매개변수 값 입니다.

기울기를 잘 이용해 손실 함수의 최솟값을 찾으려는 것이 경사하강법 입니다.

미분

우리가 찾는 손실 함수의 최솟값을 만들기 위해서는 특정 지점에서의 함수 값을 미분하고, 이를 학습률과 곱한 값을 매개변수에서 빼주게 됩니다. 미분한 값이 기울기인데, 이 기울기가 음수인지 양수인지에 따라 우리가 찾고자 하는 목적함수의 최솟값으로의 최적 매개변수의 방향을 알려줍니다.

• 미분(differentiation)은 변수의 움직임에 따른 함수값의 변화를 측정하기 위한 도구로 최적화에서 제일 많이 사용하는 기법입니다.
• 최근에는 미분을 손으로 계산하기 보다는 잘 만들어진 프로그램을 이용해 미분 값을 계산합니다.

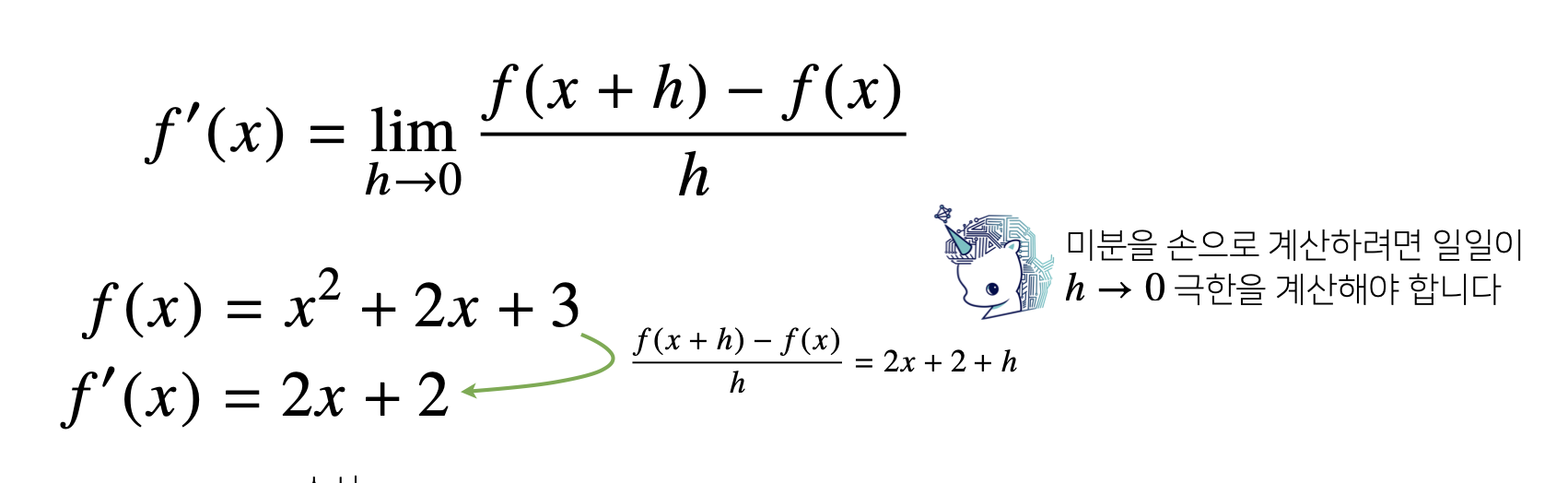
미분 값은 함수 f의 주어진 점 (x, f(x)) 에서의 접선의 기울기라고 할 수 있습니다.
한 점에서 접선의 기울기를 알면 어느 방향으로 점을 움직여야 함수값이 증가하는지/감소하는지 알 수 있습니다.

경사상승법

미분값을 더하면 경사상승법(gradient ascent)이라 하며 함수의 극대값의 위치를 구할 때 사용합니다.

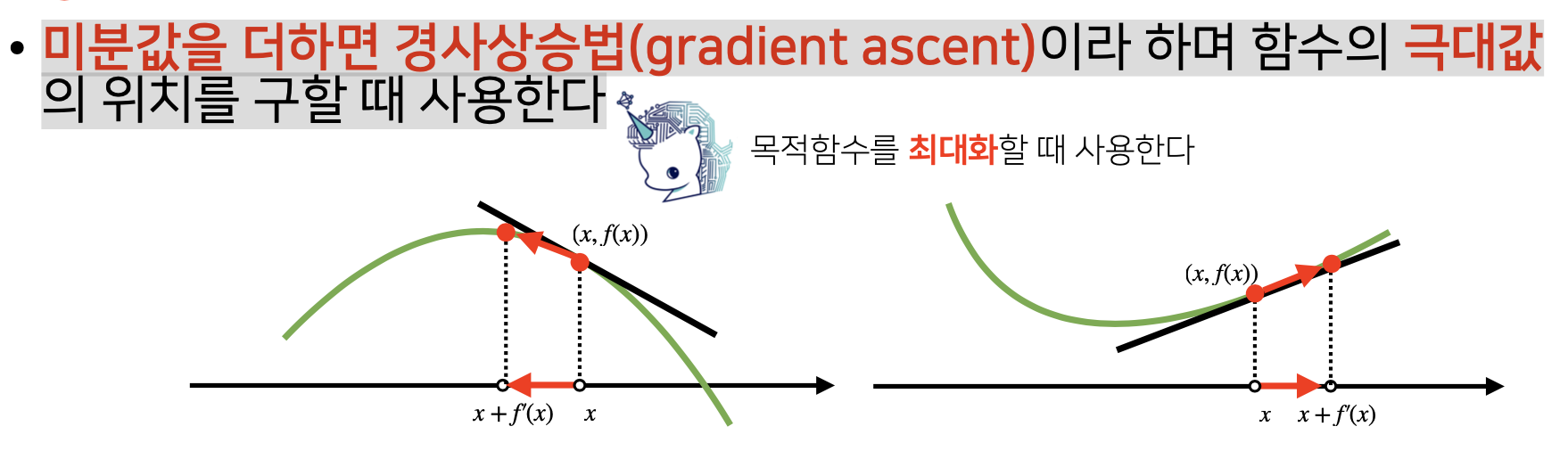
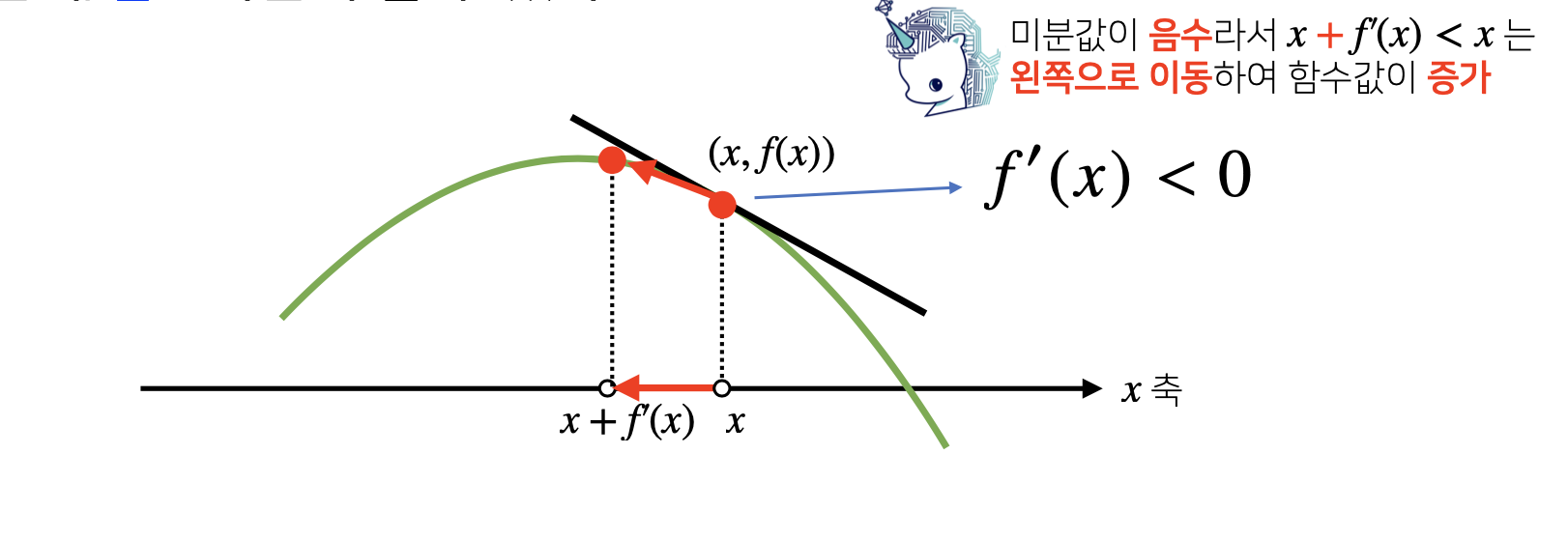
밑의 그림에서 볼 수 있듯이, 미분 값인 기울기가 음수인데, 이는 x가 감소하면 f(x)의 값은 증가를 하게 된다는 말입니다.

그래서, 경사상승법에서는 x에서 f’(x) < 0 을 더해주게 되면 x값은 감소하고, f(x)값은 증가를 하게 됩니다.

경사하강법

미분값을 빼면 경사하강법(gradient descent)이라 하며 함수의 극소값의 위치를 구할 때 사용합니다.

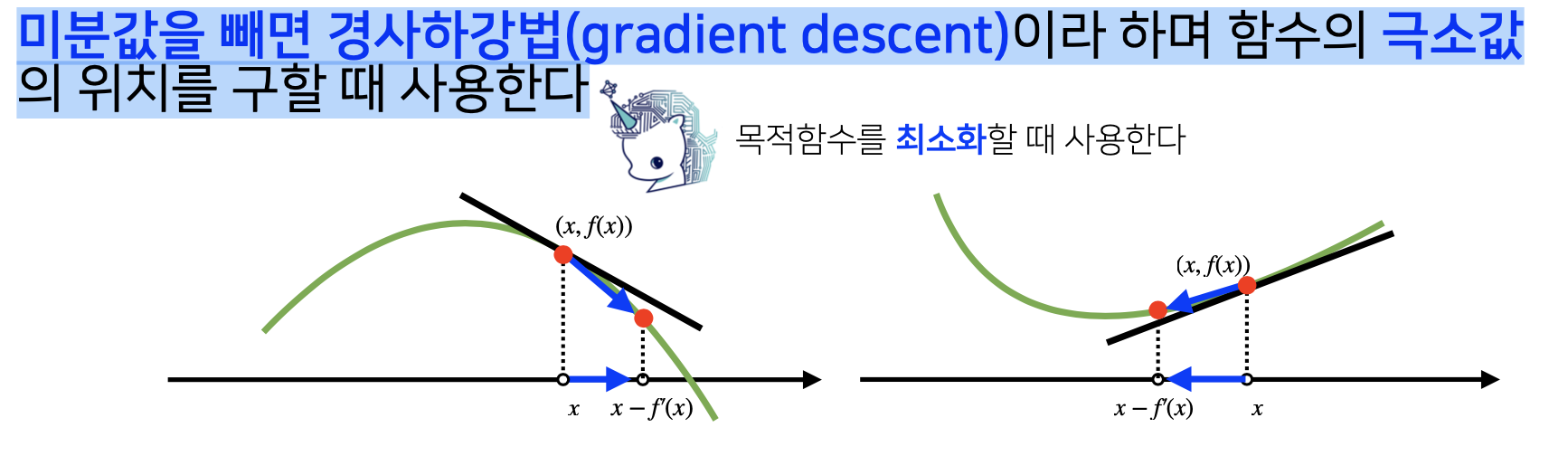
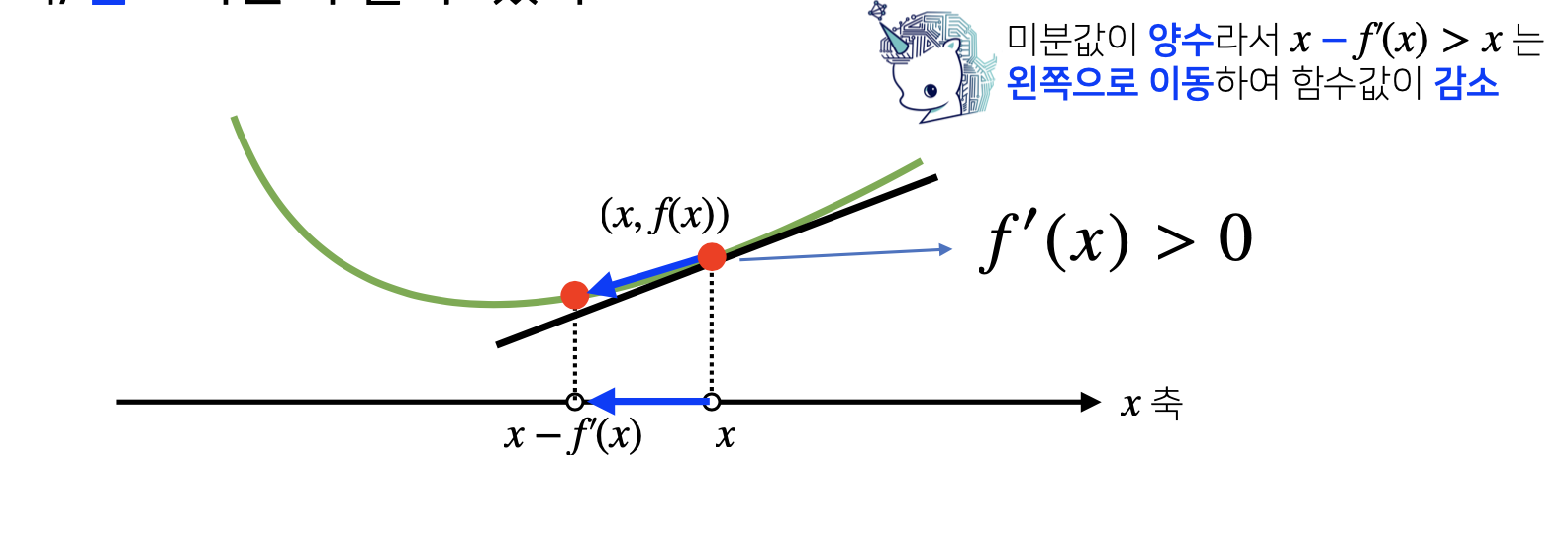
밑의 그림에서 볼 수 있듯이, 이번에는 미분 값이 양수인데, 이는 x가 감소하면 f(x)의 값도 감소를 하게 된다는 말입니다.

그래서, 경사하강법에서는 x에서 f’(x)를 빼주게 되면 x값은 감소하고, f(x)값도 감소를 하게 됩니다.

---

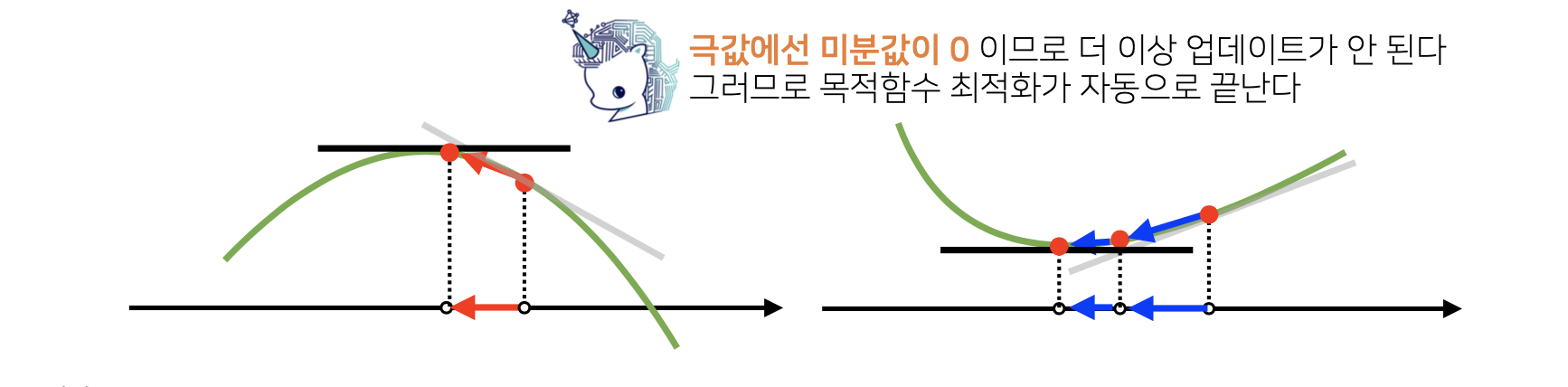
미분 값 = 기울기 = 0

경사상승/경사하강 방법은 극값에 도달하면 움직임을 멈추게 됩니다.

변수가 벡터라면

벡터가 입력인 다변수 함수의 경우 편미분(partial differentiation)을 사용하게 됩니다.

편미분이란, 미분하고자 하는 변수 이외의 다른 변수는 전부 상수로 보고 미분하는 것을 말합니다.

밑의 왼쪽식은 f(x,y)에서, 변수 x에 대해서 편미분을 한 계산입니다.
밑의 오른쪽 코드는 sympy를 이용해 다항함수의 편미분을 계산하는 것입니다.

그리고, 각 변수 별로 편미분을 계산한 그레디언트(gradient) 벡터를 이용하면 경사하강/경사상승법에 사용할 수 있습니다.

경사하강법으로 선형회귀 계수 구하기

우리가 찾고자 하는 최적의 매개변수의 개수보다 데이터의 개수가 더 많을 때 즉, n > m일 때, XW = Y 에서, 우리는 W를 X의 유사역행렬을 구해 다음과 같은 식으로 구할 수 있었습니다. $W = X^{+}Y$

또 다른 방법은 경사하강법을 이용하여 구할 수도 있습니다.
선형회귀의 목적식은 ∥y − Xβ∥2 (손실 함수) 이고 이를 최소화하는 β를 찾음으로 구할 수 있고, 우리는 이 β를 구하기 위해 다음과 같은 그레디언트 벡터를 구해야 합니다.

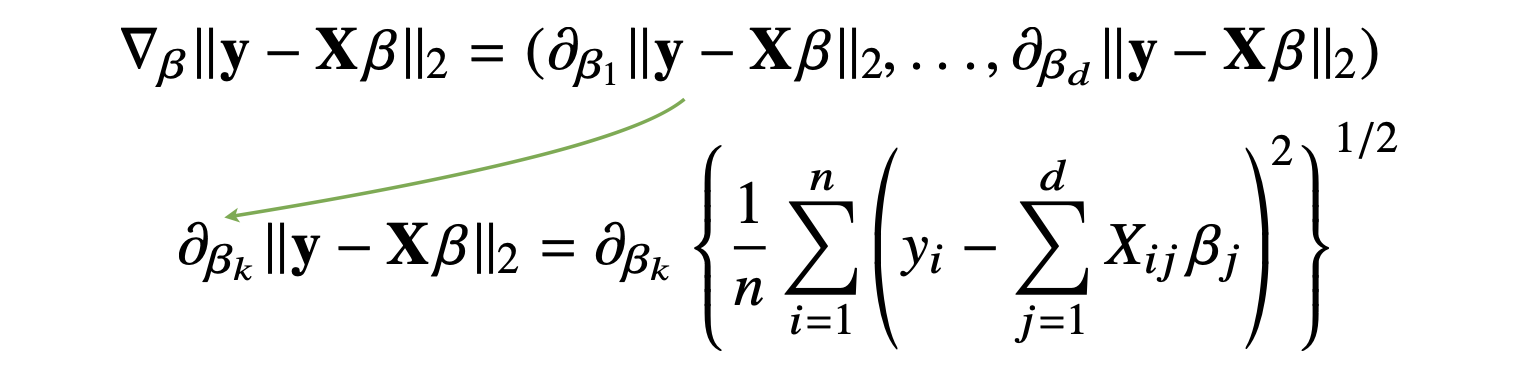
주의할 점은 y-Xβ의 L2 노름과 비슷하지만, 여기서는 레이블 값(y)과 예측 값(Xβ)의 차이의 제곱을 한다음 전부를 더해 전체 데이터의 개수로 나누어줬다는 점입니다.
이렇게 기존의 L2 노름에서 전체 데이터의 개수로 나누주었을 때는, 이 손실 함수를 평균이 들어간 평균 최소 제곱 오차 - mean square error 라고 합니다.

위의 식에 대해서 모든 매개변수 벡터에 대해 각각 편미분을 해서 정리하면 밑의 그림과 같은 식을 얻을 수 있습니다.

복잡해 보이지만, 기본적인 미분(겉미분, 속미분)과 편미분을 할줄 알고 스칼라 백터 미분을 할줄 아신다면 충분히 식을 유도해 낼 수 있습니다.

그리고 목적식을 최소화하는 β를 구하는 경사하강법은 위에서 본 것과 똑같이 적용할 수 있습니다.

경사하강법의 문제

이론적으로 경사하강법은 미분가능하고 볼록(convex)한 함수에 대해선 적절한 학습률과 학습횟수를 선택했을 때 수렴이 보장되어 있습니다.

특히 선형회귀의 경우 목적식 ∥y − Xβ∥2 은 회귀계수 β 에 대해 볼록함 수이기 때문에 알고리즘을 충분히 돌리면 수렴이 보장됩니다.

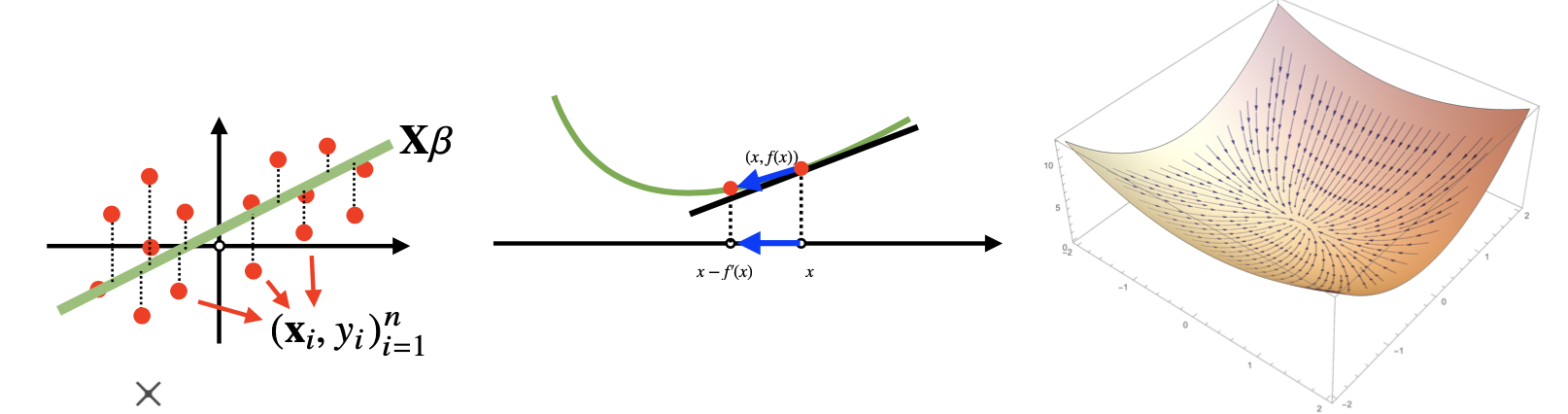
하지만 비선형회귀 문제의 경우 목적식이 볼록하지 않을 수 있으므로 수렴이 항상 보장되지는 않습니다.
전역 최적해가 아닌 지역 최적해에 빠질 수도 있기 때문입니다.

확률적 경사하강법

위에서 본, 경사하강법의 문제를 보완하기 위해 나온 것이 확률적 경사하강법이란 것입니다.

확률적 경사하강법(stochastic gradient descent)은 모든 데이터를 사용해 서 업데이트하는 대신 데이터 한개 또는 일부 활용하여 업데이트합니다.

그래서, 볼록이 아닌(non-convex)목적식도 SGD를 통해 최적화할 수 있습니다

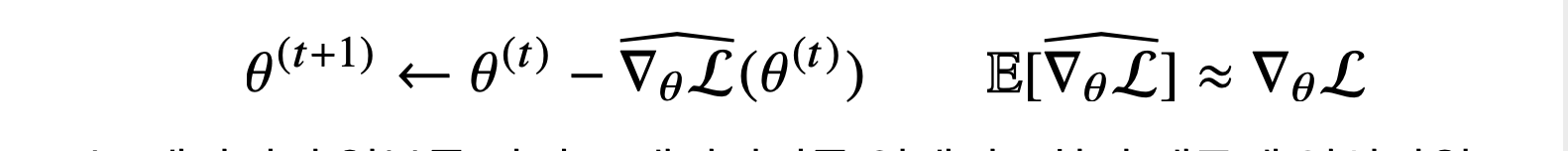
즉, 확률적 경사하강법의 원리는 미니배치 연산에 있습니다.

경사하강법은 전체데이터 𝒟 = (X, y) 를 가지고 목적식의 그레디언트 벡터인 ∇θL(𝒟,θ)를 계산하는 데 반해, SGD 는 미니배치 𝒟(b) = (X(b), y(b)) ⊂ 𝒟 를 가지고 그레디언트 벡터를 계산합니다.그래서, 미니배치는 확률적으로 선택하므로 목적식 모양이 랜덤하게 바뀌게 됩니다.

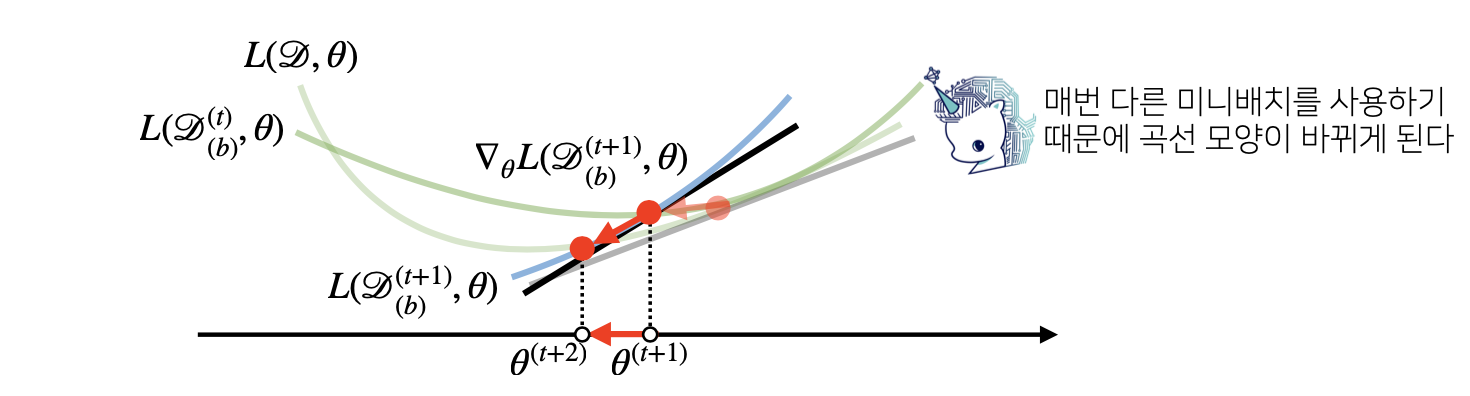
만역 목적함수가 Non convex한 함수이고, 일반적인 경사하강법을 적용하면 전역최적해에 도달하기 전에 지역 최적해에 빠져 계산이 멈출 수도 있습니다. 이는 모든 데이터 셋을 활용하여 계산한 값으로서 더 이상 이 지역 최적해에서 벗어날 수가 없습니다.

하지만 확률적 경사하강법은 매 연산마다 랜덤한 샘플의 미니배치를 뽑아 그레디언트를 계산 하므로, 우리의 목적 함수의 형태가 매번 바뀌게 되고, 이는 확률적으로 지역 최적해 에서 벗어나 전역 최적해에 도달하게 합니다.

피어세션 정리

두 번째 주차 둘째 날 모임이었습니다.
오늘은 어제의 룰에 따라 다 같이, further question 논의 해보기로 하였습니다.
오늘의 further question은 주어진 목적함수의 그레디언트를 손으로 계산해보기 였습니다.
이 문제에 대해 각자 어떻게 방법을 적용하였는지 논의 할 수 있었고, 또 이 문제가 어렵다는 분도 다른 분의 해설과 해결 방법을 듣고 “아하” 소리가 나올 만큼 의미가 있는 시간이 되었던거 같습니다.
나머지 시간은 앞으로 다뤄질 역전파, 통계학 등등에 대해 논의하였고, 서로 공부하기 전에 찾아보거나 좋은 리소스가 있으면 공유하는 시간을 가졌었습니다.

퀴즈 정리

벡터

1. $f(x,y)$가 다음과 같이 정의될 때, $\frac{ \delta f(x,y) }{ \delta x }$를 구하시오 (정수값으로 입력).

   $f(x,y)=9y^{2}+3y+9x+3$

   이는 x에 대해서 편미분 하라는 뜻이고, x 이외의 나머지 변수에 대해서는 전부 상수로 보고 미분을 진행하면 되는 문제였습니다.

2. 미분이 가능한 함수 $f$ 에 대해, 주어진 점 $(x, f(x))(x,f(x))$ 에서의 접선의 기울기가 음수라면, $x$ 를 증가시키면 함수값 $f(x)$가 증가한다? (O,X 문제)

   기울기가 음수라면, x값이 증가할 때는 반대로 함수의 값은 감소하게 됩니다.

3. 다음 보기 중 함수의 극소값의 위치를 구할 때 사용하는 방법을 고르시오.

   여러개의 보기 중 위에서 우리는 함수의 극소값의 위치를 구할 때 사용하는 방법을 공부했고, 이에 따라 배운 내용을 고르면 되는 문제였습니다.

4. 경사하강법을 사용하여 구한 함수의 극소값의 위치는 해당 함수의 최소값의 위치가 아닐 수 있다.

   경사하강법을 이용한 극소값은 Non convex(볼록하지 않은 함수)에서 지역해에도 해당이 될 수 있습니다. 그래서 최소값의 위치가 아닐 수도 있습니다.

5. 다음 보기 중 $f(x, y, z)$의 올바른 그래디언트 벡터를 고르시오.

   $f(x,y,z)=9x^{2}+5y^{3}−3z$

   변수 $x,y,z$에 대해 각각 편미분 한 값의 벡터가 답이 됩니다.

   $x$에 대해서 편미분하면 첫 번째 텀인 $18x$가 계산되고 나머지는 상수 취급되어 사라집니다.
   $y$에 대해서 편미분하면 두 번째 텀인 $15y^{2}$가 계산되고 나머지는 상수 취급되어 사라집니다.
   $z$에 대해서 편미분하면 세 번째 텀인 $-3$이 계산되고 나머지는 상수 취급되어 사라집니다.

References

• Mathematics for Artificial Intelligence - Unist 임성철 교수님