Numpy / 벡터 / 행렬

Numpy / 벡터 / 행렬

넘파이는 과학계산에서 많이 사용하는 선형대수의 계산식을 파이썬으로 구현할 수 있도록 도와주는 라이브러리입니다. 모든 데이터 분석과 인공지능 학습에 있어 가장 필수적으로 사용되고 이용되므로 간단한 예제들과 함께 알아봅니다.

벡터는 딥러닝에서 매우 중요한 선형대수학의 기본 단위가 되고, numpy에서도 굉장히 많이 사용되는 연산이기 때문에 확실하게 알 필요가 있습니다.

행렬은 딥러닝에서 가장 핵심적인 연산이라고 볼 수 있을만큼 중요하고, 자주 사용됩니다.
행렬이 가지는 기하학적 의미와 머신러닝에서 어떻게 사용되는지 알아봅니다.

Numpy

넘파이는 과학계산에서 많이 사용하는 선형대수의 계산식을 파이썬으로 구현할 수 있도록 도와주는 라이브러리입니다.

• Numerical Python
• 파이선의 고성능 과학 계산용 패키지
• Matrix와 Vector 와 같은 Array 연산의 사실상의 표준

특징

• 일반 리스트에 비해 빠르고 효율적
• 반복문 없이 데이터 배열에 대한 처리 지원
• 선형대수와 관련된 다양한 기능을 제공

import

넘파이의 호출 방법입니다.
일반적으로 np라는 별칭을 이용해서 호출합니다. (세계적인 약속 같은 것)

import numpy as np

array creation

test_array = np.array([1, 4, 5, 8], float)
print(test_array)
# array([1., 4., 5., 8.])

넘파이는 np.array라는 함수를 활용해서 배열을 생성합니다.
넘파이에는 하나의 데이터 타입만 배열에 넣을 수 있습니다.

array shape

• shape : array의 크기, 형태 등에 대한 정보

다른 프로그래밍 언어와 같이 다음과 같이 선언하고 특정 값으로 초기화 할 수 있습니다.

arr_shape = np.array([[1,2,3,4],[1,2,3,4]]).shape
print(arr_shape)
# (2,4)

• ndim - number of dimension
• size - number of data(element)

array type

• array의 single element가 가지는 데이터 타입
• 각 element가 차지는 메모리의 크기가 결정됨
• int8, int16, float32, float64, str 등이 있습니다.

array reshape

• reshape : Array의 shape의 크기를 변경할 수 있습니다. size는 동일.

다음은 2x4의 매트릭스를 1차원의 원소 8개를 가지는 벡터로 변환하는 코드입니다.

arr = np.array([[1,2,3,4],[1,2,3,4]])
np.array(arr).shape
# (2, 4)
np.array(arr).reshape(8,)
# array([1, 2, 3, 4, 1, 2, 3, 4])
np.array(arr).reshape(8,).shape
# (8,)

indexing for numpy array

리스트와 달리 2차원 배열에서 [0, 0]표기법을 제공합니다.
매트릭스일 경우는 앞은 row, 뒤는 column을 의미합니다.

a = np.array([[1, 2, 3], [4.5, 5, 6]], int)
print(a)
print(a[0,0]) # Two dimensional array representation #1
print(a[0][0]) # Two dimensional array representation #2
a[0,0] = 12 # Matrix 0,0 에 12 할당 print(a)
a[0][0] = 5 # Matrix 0,0 에 12 할당 print(a)

리스트와 달리 행과 열 부분을 나워서 슬라이싱이 가능합니다.
이는 매트릭스의 부분집합을 추출할 때 유용합니다.

a = np.array([[1, 2, 3, 4, 5], [6, 7, 8, 9, 10]], int)
a[:,2:] # 전체 Row의 2열 이상
# array([[3, 4, 5], [8, 9, 10]])
a[1,1:3] # 1 Row의 1열 ~ 2열
# array([7, 8, 9])
a[1:3] # 1 Row ~ 2Row의 전체
# array([6, 7, 8, 9, 10])

arange

array의 범위를 지정하여, 값의 list,fmf 생성하는 명령어 입니다.

np.arange(5) # array([0, 1, 2, 3, 4])
np.arange(1, 5) # array([1, 2, 3, 4])

np.arange(1,5).reshape(2, 2)
# array([[1, 2], [3, 4]])

zeros, ones

0또는, 1로 채워진 ndarray를 생성하는 함수

#zeros :
np.zeros(shape=(5,))
# array([0, 0, 0, 0, 0])
np.zeros(shape=(2,2))
# array([[0, 0],
#        [0, 0]])

#ones :
np.ones(shape=(3,))
# array([1,1,1])

sum / mean / std

ndarray의 element들 간의 합을 구하거나 평균 또는 표준편차를 구하는 기능의 함수입니다.

arr = np.arange(1,5).sum(dtype=np.int)
# 10

test_array np.arange(1, 13).reshape(3, 4)
test_array
# array([[1,2,3,4],
#         5,6,7,8],
#         9,10,11,12)

test_array.mean()
# 6.5

test_array.std()
# 3.4520525295346629

이 외에도 다양한 수학 연산자 함수를 제공합니다.

ex) exp, log, log10, power, sqrt, sin cos, tan, cosh…

Dot product

매트릭스의 dot product 계산에 쓰이는 함수입니다.

test_a = np.arange(1, 7).reshape(2, 3)
test_b = np.arange(7, 13).reshape(3, 2)

test_a.dot(test_b)
# array([[58, 64], [139, 154]])

broadcasting

shape이 다른 배열 간 연산을 지원하는 기능입니다.

test_matrix = np.array([[1,2,3],[4,5,6]])
scalar = 3
#덧셈
test_matrix + scalar
# array([[4, 5, 6],
#        [7, 8, 9]])

# 곱셈
test_matrix * scalar
# array([[3, 6, 9],
#        [12, 15, 18]])

All & Any

a = np.arange(10)
a # array([0, 1, 2, 3, 4, 5, 6, 7, 8, 9])
np.any(a>5), np.any(a<0)
# (True, False)
np.all(a>5), np.any(a<10)
# (False, True)

벡터

벡터는 숫자를 원소로 가지는 리스트 또는 배열이라고 볼 수 있습니다.

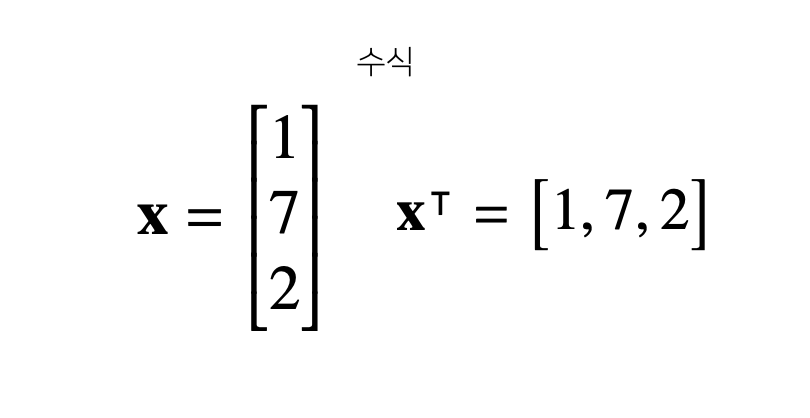
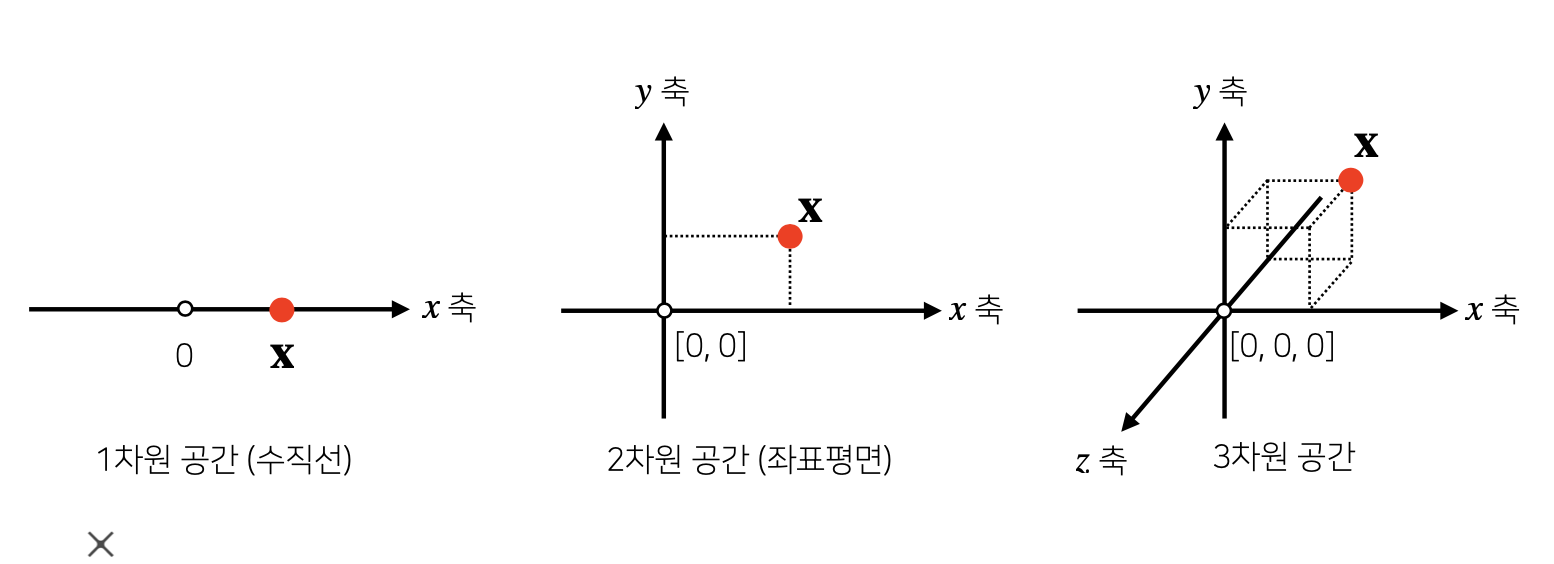
벡터는 공간에서 한점을 나타냅니다.

벡터는 숫자르 원소로 가지는 리스트로서 백터끼리 같은 모양을 가지면 덧셈, 뺄셈, 성분곱이 가능합니다.

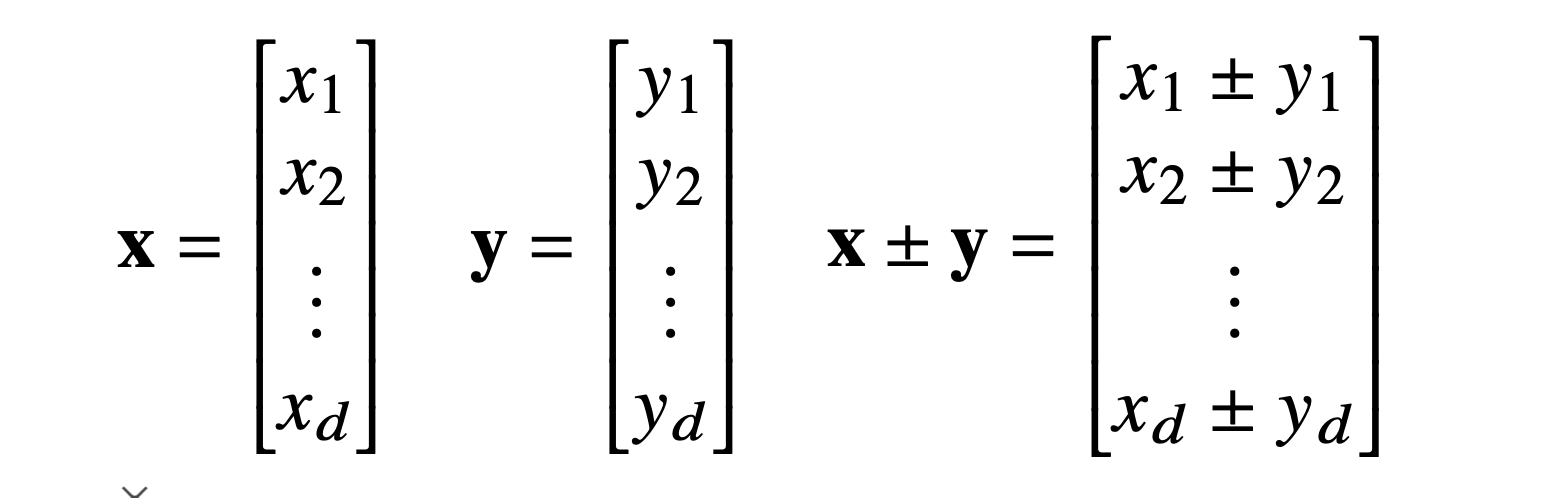
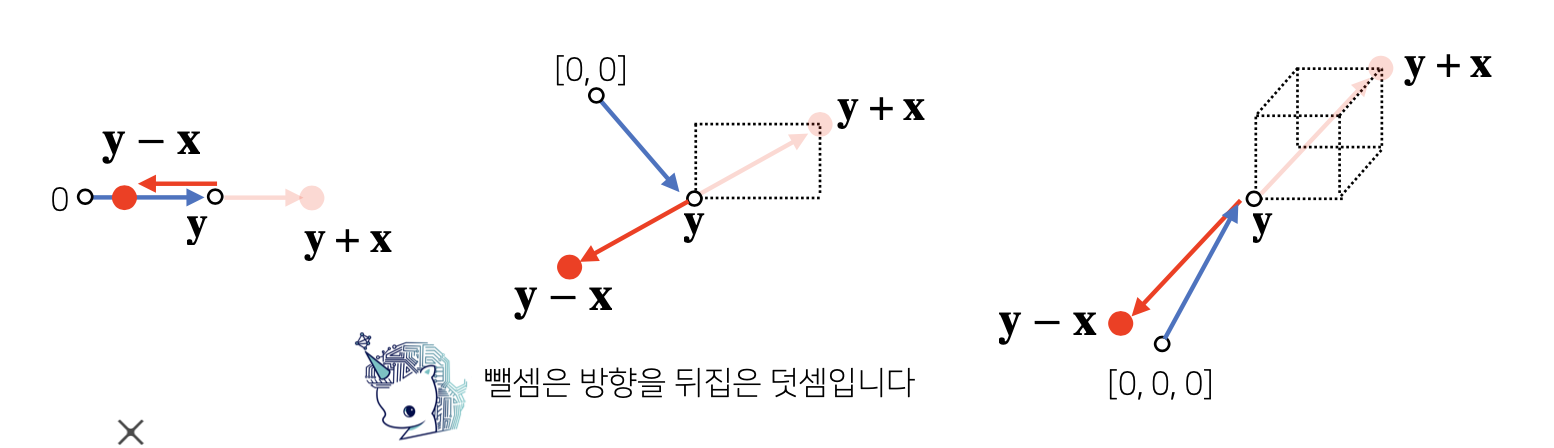
벡터의 뺄셈

두 벡터의 뺄셈은 다른 벡터로 부터 상대적 위치이동을 표현합니다.
벡터의 뺄셈은 방향을 뒤집은 덧셈입니다.
대수적으로 보면 : x = [1 ,2], y = [5, 3] 이란 두개의 벡터가 있을 때 y - x 뺄셈을 하면 -> [4, 1]이 됩니다.

백터의 노름

벡터의 노름은 원점에서부터의 거리를 말합니다.

L1 노름과 L2노름이 있습니다.

• L1-노름은 각 성분의 변화량의 절대값을 모두 더합니다.
• L2-노름은 피타고라스 정리를 이용해 유클리드 거리를 계산합니다.

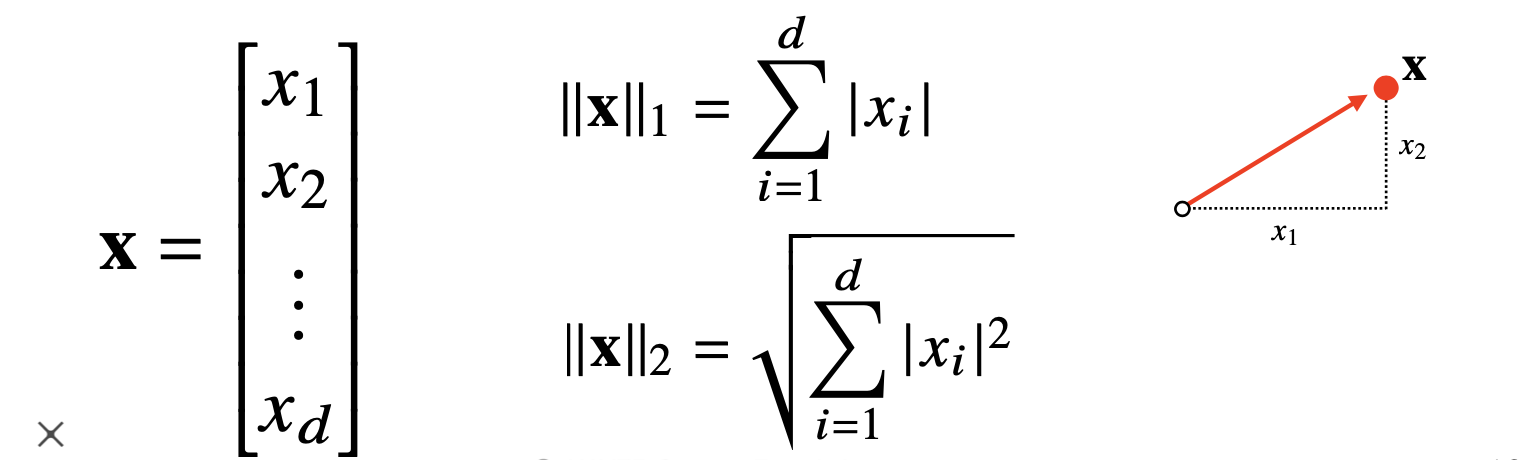
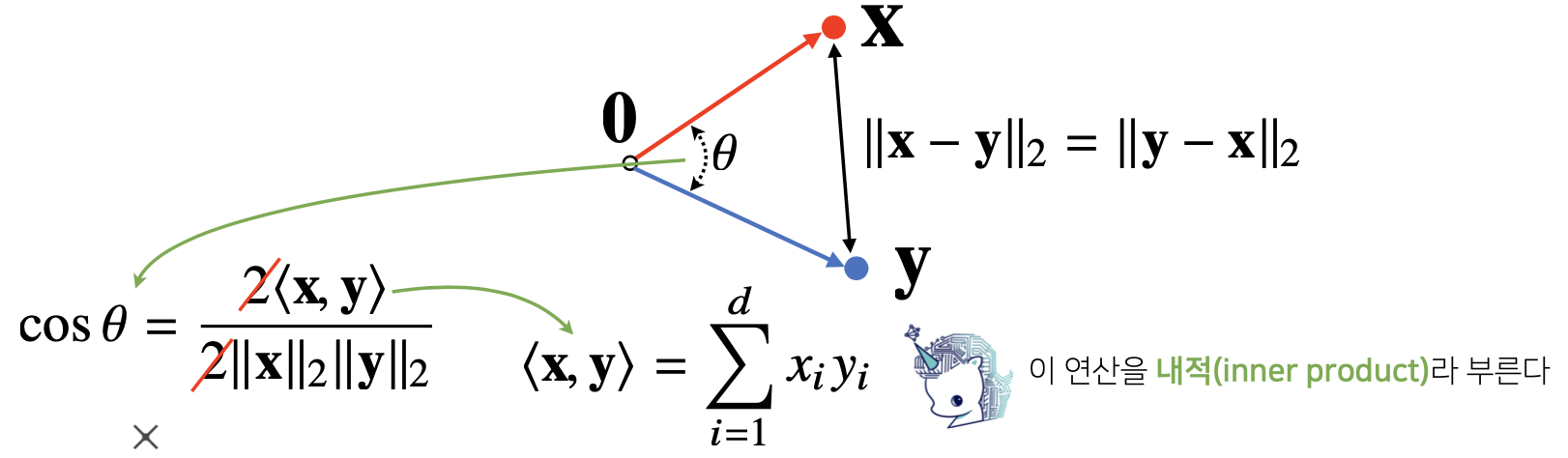
두 벡터 사이의 각도 구하기

두 벡터 사이의 거리는 제2 코사인 법칙에 의해 두 벡터 사이의 각도를 계산 가능
그리고 분자는 더욱 간단히 내적으로 구할 수 있다.

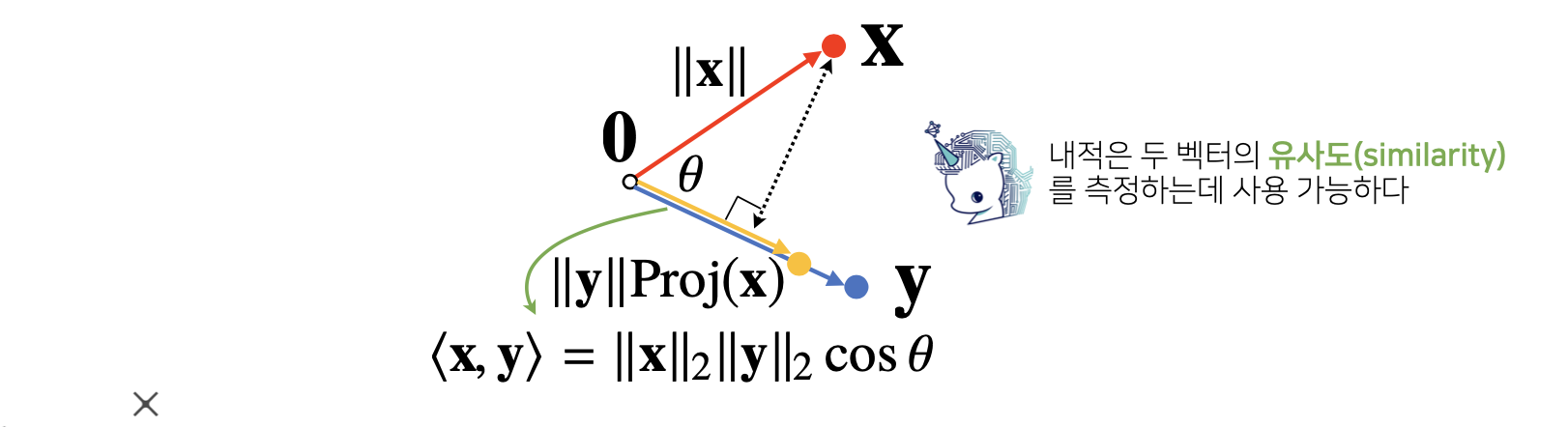
내적 해석하기

내적은 정사영된 벡터의 길이와 관련 있다.
proj(x)의 길이는 코사인 법칙에 의해 x의 노름 x cos(theta)가 된다.
내적은 정사영의 길이를 벡터 y의 길이 만큼 조정한 값이 된다.

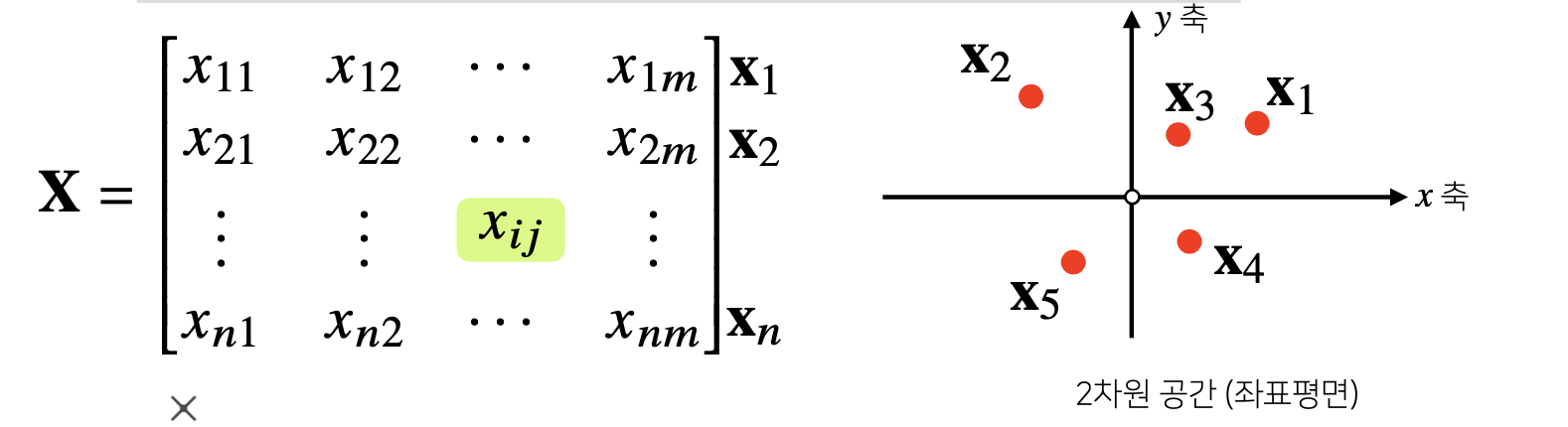
행렬

• 행렬(matrix)은 벡터를 원소로 가지는 2차원 배열입니다.
• 행렬은 행(row)과 열(column)이라는 인덱스(index)를 가집니다.
• 행렬의 특정 행(열)을 고정하면 행(열)벡터라 부릅니다.

• 벡터가 공간에서 한 점을 의미한다면 행렬은 여러 점들을 나타냅니다.
• 행렬의 행벡터 xi 는 i 번째 데이터를 의미합니다.
• 행렬의 xij 는 i 번째 데이터의 j 번째 변수의 값을 말합니다.

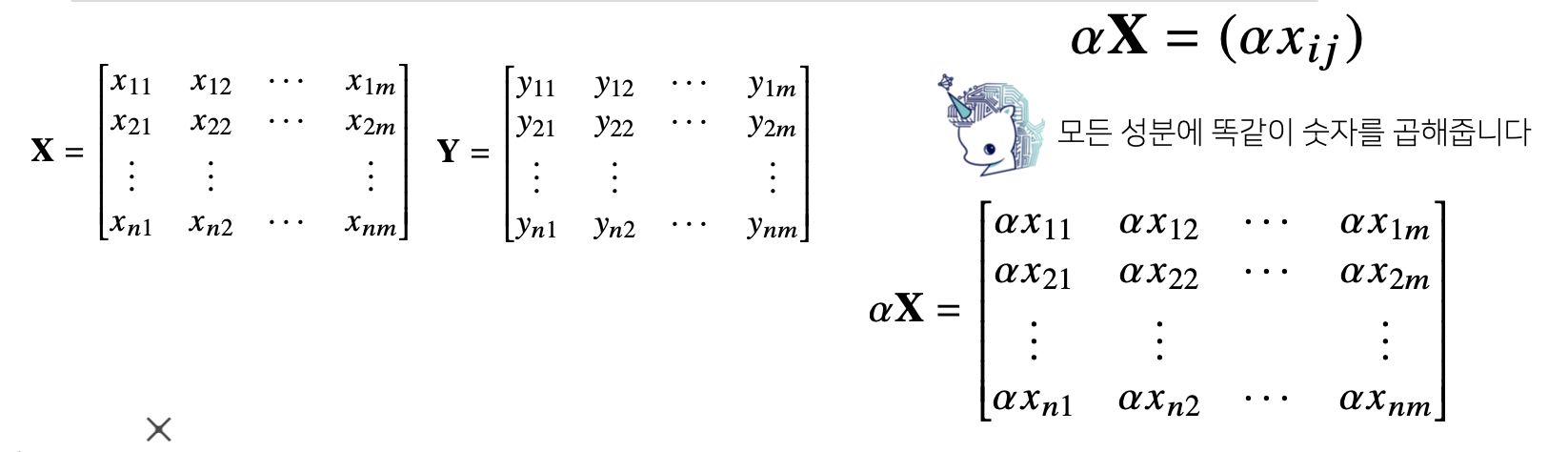
행렬에서의 스칼라곱

• 성분곱은 벡터와 똑같습니다. 스칼라곱도 벡터와 차이가 없습니다.

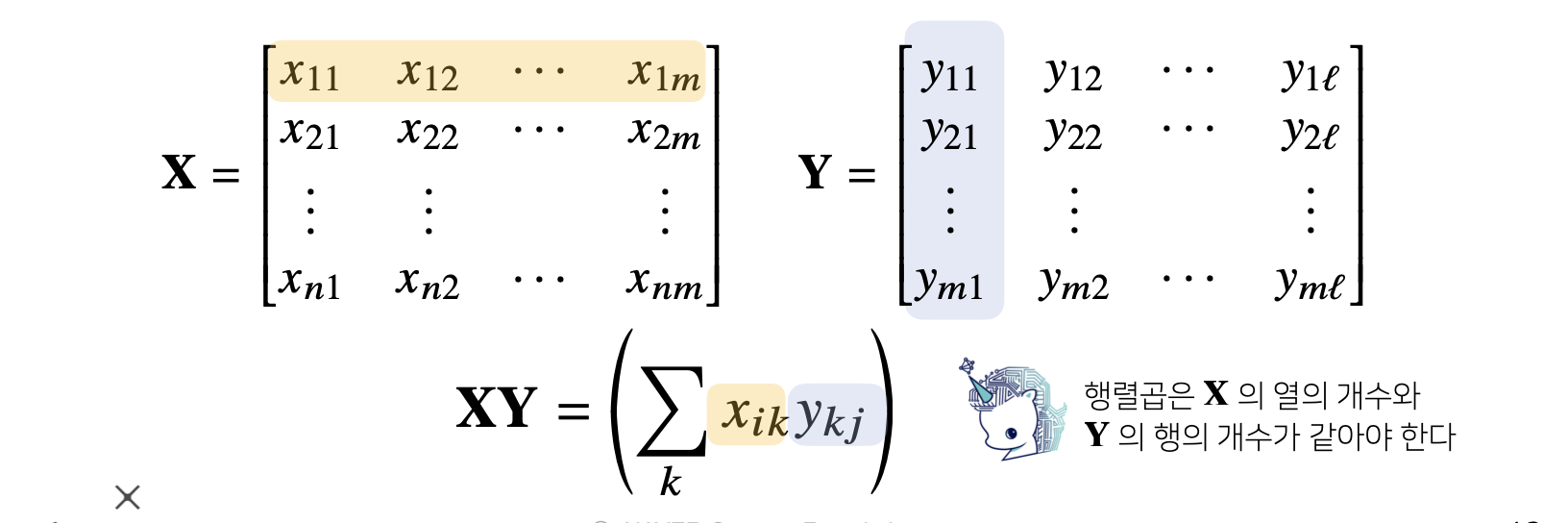
행렬에서의 곱셈

행렬 곱셈은 i번째 행벡터와 j번째 열벡터 사이의 내적을 성분으로 가지는 행렬을 계산합니다.

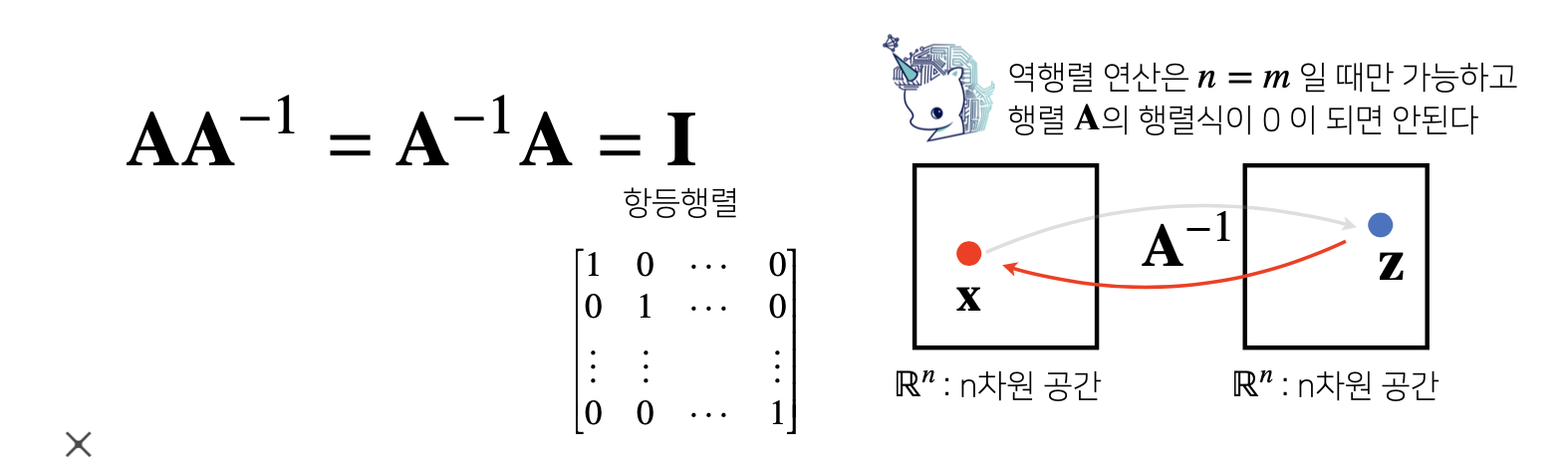
역행렬 이해하기

• 어떤 행렬 A 의 연산을 거꾸로 되돌리는 행렬을 역행렬(inverse matrix)이 라 부르고 A−1 라 표기한다.
  역행렬은 행과 열 숫자가 같고 행렬식(determinant)이 0이 아닌 경우에만 계산할 수 있다. (ad-bc != 0)

• 만일 역행렬을 계산할 수 없다면 유사역행렬(pseudo-inverse) 또는 무어-펜로즈(Moore-Penrose) 역행렬 A+ 을 이용한다.

피어세션 정리

두번째 주차 첫 날 모임이었습니다.
오늘은 새로운 모더레이터가 선출되고, 부스트캠프의 시간표가 조금 바뀜에 따라 피어 플랜을 다시 재정비 하기로 했습니다.
회의를 통해 의견이 모아졌고, 기존에 하던 “어제 무엇을 하였고, 오늘의 공부 계획은?” 계속 진행하고, 이제 edwith에는 오늘 다룬 토픽에 대해 좀 더 알아보기란 목록으로 “further question”이 추가 된다고 하여, 이와 묶어 당일 다뤄진 내용 중 다소 어렵거나 이해가 안간 내용과 같이 피어들과 같이 회의하고 공부하기로 하였습니다.

퀴즈 정리

벡터

1. 다음 백터의 L-1 노름을 구하라.

   x=[−1,2,−3]

   각 요소의 절대값의 합이 답이 됩니다.

2. 다음 백터의 L-2 노름을 구하라.

   x = [-6, -8]x=[−6,−8]

   각 요소의 제곱의 총합에 제곱근을 취한 값이 답이 됩니다.

3. L2-노름을 이용하여 다음 두 벡터 사이의 거리를 구하시오 (정수값으로 입력).

   x=[−3,0]
   y=[0,4]

   두 벡터의 뺄셈을 하여 L-2 노름을 취한 값이 거리가 됩니다.

4. 다음 두 벡터 사이의 각도를 구하시오 (라디안 단위: 0 이상, 7 미만의 정수값으로 입력)

   x=[0,1] y=[0,2]

   theta = arccos * (x와y의 내적) / (x의 노름 * y의 노름)으로 구해도 되고,
   이 벡터의 경우에는 두 벡터가 정확히 같은 방향(포개어져 있음)이므로 각이 0도 입니다.

5. 내적이 다음과 같이 정의될 때, 다음 두 벡터 ( x, y )의 내적을 구하시오 (정수값으로 입력).

   x=[1,−1,1,−1] y=[4,−4,4,−4]

   [x, y] 의 내적 = x의 노름 * y의 노름 * cos(theta)로 구할 수 있습니다.

행렬

1. 다음 보기 중 행렬 X 의 올바른 전치행렬을 고르시오.

   T한 행렬을 구하라는 의미입니다.
   성분 i와j를 서로 바꾸어준 위치를 생각하면 됩니다.

2. 두 행렬의 곱셈은 각 행렬의 모양과 상관없이 가능하다? (O,X) 문제

   두 행렬의 곱셈은 앞의 행렬의 열과 뒤의 행렬의 행의 개수가 맞아야 합니다.

3. 어떠한 행렬의 역행렬은 항상 계산할 수 있다. (O,X) 문제

   2차원 정사각행렬을 예로 들면, ad-bc = 0 이 아니면 역행렬이 존재하지 않습니다.

4. 다음 보기 중 행렬 XX 의 올바른 역행렬을 고르시오.

   수반행렬을 사용해 구해도 되고, 가우스 조던 소거법을 이용해 풀어도 좋습니다.
   어떤분은 넘파이 함수를 이용해 푸셧다고 합니다.

5. 다음 보기 중 행렬 X 의 올바른 무어-펜로즈 역행렬을 고르시오.

   저는 강의에서 배운대로 $A = A^{+}b = A^{T} \big(AA^{T}\big)^{-1}b$를 하여 답을 구할 수 있었습니다.

References

• Mathematics for Artificial Intelligence - Unist 임성철 교수님