Gyeong

Gyeong

It is in the moment of decisions that your destiny is shaped.

Union-Find

컴퓨터 과학에서 서로소 찾기 집합 혹은 병합 찾기 집합이라 불리며 중복되지 않은 부분집합들의 원소 정보를 조작하고 저장하는 자료구조이다.

부분집합(Subset)에서 특정 원소 하나를 A, 또 다른 원소 하나를 B라 하면, 이 A나 B가 어느 부분집합에 속하는지, 또 A와 B가 각각 속한 부분집합 다르다면 이 두 부분집합을 하나의 집합으로 합쳐, 원소들이 겹치지 않는(Non-overlapping) 하나의 부분집합을 구성하는 것에 목적이 있다.

Representation

유니온 파인드 자료구조는 트리로 표현이 될 수 있습니다. 처음 N개의 원소 각각은 서로 다른 1개의 트리이자 부분집합이며 자기 자신이 최상위 루트이다. 각각의 부분집합을 구별할 땐 그 부분집합의 루트를 이용한다. 서로 다른 두개의 부분집합을 합칠 땐 하나의 부분집합의 루트를 다른 하나의 부분집합의 루트로 가리키게 한다.

Union-Find represented as a tree:

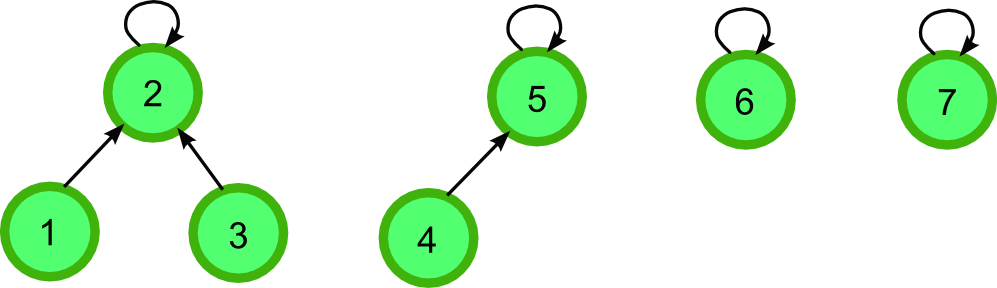
Alt text

우리는 이를 “1 Dimention Array”로 표현이 가능하다.

index i	  =  1, 2, 3, 4, 5, 6, 7 
parent[i] = [2, 2, 2, 5, 5, 6, 7]

parent[1] = 2 -> 원소 1은 원소 2를 부모로 한다.
parent[6] = 6 -> 원소 6은 6 즉, 자기 자신을 부모로 한다.

Operations

다음은 유니온 파인드 자료구조를 위한 연산들이다.

Make set (Initialization)

유니온 파인드 자료구조를 위한 새로운 집합을 생성한다.
노드 각각이 자기 자신을 가리키도록 설정한다. (처음에는 자기 자신이 트리의 최상위 노드)

public void makeSet() {
   for (int i = 0; i < n; i++)
     parent[i] = i;
}

Make set operation:

Alt text

배열의 상태는 아래와 같다.

index i   =  1, 2, 3, 4, 5, 6, 7
parent[i] = [1, 2, 3, 4, 5, 6, 7]

Find

우리는 두 원소가 서로 다른 부분집합에 속해있으면 두 부분집합을 Union 할 수 있다.
두 원소가 서로 같은 부분집합에 포함되어 있는지 아닌지 확인하기 위해 두 원소의 루트를 확인해야 한다.
Find 연산은 해당 원소가 속해있는 부분집합의 루트를 반환한다.

  1. 원소 x의 부모가 자기 자신이라면 그 부분집합의 루트이므로 x를 반환한다.
  2. 아니라면 재귀 호출로 x의 부모를 따라간다.
  3. 루트를 찾을 때까지 재귀 호출이 진행되다가 루트를 찾으면 원소 x의 루트를 반환한다.
int find(x) { // Recursive function
    if (parent[x] == x)    // 원소 x의 부모가 자기자신이면 그 부분집합의 루트이므로
       return x;        // x를 반환합니다.
    else   
       return find(parent[x]); // 아니라면 x의 부모를 다시 재귀호출하여 루트를 찾습니다.
}

Find(1) returns 2:

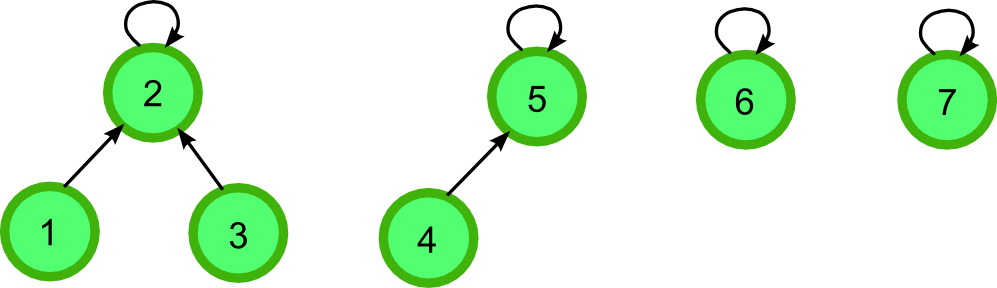
Alt text

다음은 현재 배열의 상태이다.

index i   =  1, 2, 3, 4, 5, 6, 7
parent[i] = [2, 2, 2, 5, 5, 6, 7]

원소 1이 속한 부분집합의 루트를 알고 싶다면 Find(1)을 수행한다.
parent[1] != 1 두 값이 같지 않다.
그럼 parent[1]을 매개변수로 다시 Find(parent[1])을 재귀 호출한다.// 이는 부모를 따라가는 것이다.
parent[2] == 2 두 값이 같다! 2를 반환한다.
1의 루트는 2 임을 알 수 있다.

5를 보면.
find(5)를 수행하면 parent[5] == 5 두 값이 같다.
5의 부모는 5 자기 자신의 값이 되고, 이 말은 자기 자신이 루트란 말이므로 5를 반환한다.

Union

두 원소가 속한 부분집합이 다르면 두 부분집합을 하나의 부분집합으로 합칠 수 있다.
이를 수행하는 연산이 Union이다.

  1. 두 원소(x, y)가 속한 부분집합이 서로 같다면 return 한다.
  2. 같지 않다면 두 부분집합을 합친다.

Make set operation:

Alt text

처음에 이렇게 7개의 서로 다른 부분집합이 있다. (자기 자신이 트리의 루트)

Union:

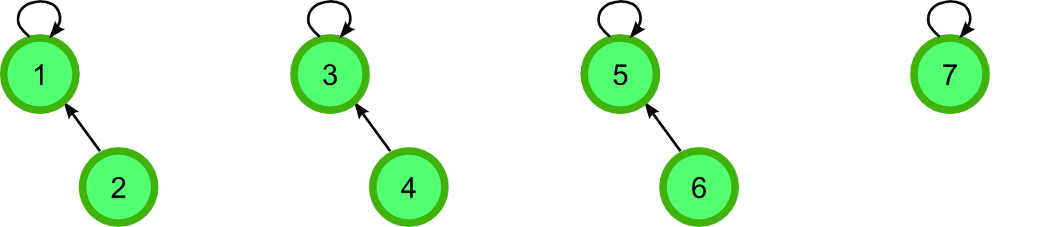
Alt text

union(2,1), union(4,3), union(6,5)를 수행하면 위 그림처럼 트리가 구성된다.
2의 루트는 2이고 1의 루트도 1 자기 자신이다.
둘의 값이 다르므로 서로 다른 부분집합이고, 2는 1을 가리킴으로써 부분집합을 합친다.
union(4,3), union(6,5)도 마찬가지이다.

다음은 위 트리의 배열 상태이다.

index i   =  1, 2, 3, 4, 5, 6, 7
parent[i] = [1, 1, 3, 3, 5, 5, 7]

union(2, 4)를 하면 아래 그림처럼 된다.

Union(2, 4):

Alt text

void union(int x, int y) {
    xRoot = find(x) // find로 x의 루트를
    yRoot = find(y) 
    if(xRoot == yRoot) // 두 원소가 속한 부분집합이 같으므로 리턴합니다.
      return;
    parent[x_root] = y_root; // 두 부분집합을 합칩니다. x의 루트를 y의 루트로 가리키게 합니다.
}

2가 속한 부분집합의 루트(find(2))는 1이고, 4가 속한 부분집합의 루트(find(4))는 3이므로, 이 둘의 값이 다르고 1이 3을 가리킴으로써(parent [1] = 3) 같은 부분집합으로 합쳐준다.

아래는 위 트리의 배열 상태이다.

index i   =  1, 2, 3, 4, 5, 6, 7
parent[i] = [3, 1, 3, 3, 5, 5, 7]

Path compression

부분집합을 합치는 연산(유니온)을 수행하면서 아래 그림과 같이 편향적인 트리로 구성될 수 있다.
이때 노드의 개수가 n개일 때 find(n)을 수행하면 시간 복잡도는 $O(n)$가 된다.
아래 그림에서 5번 원소는 자기 부모를 타고 가다가 끝에는 루트 1을 만나게 된다. 링크를 4번 타고 가야 루트를 찾을 수 있다.
4번 원소도 링크를 3번 타고 가야 루트를 찾을 수 있다.

편향 트리:

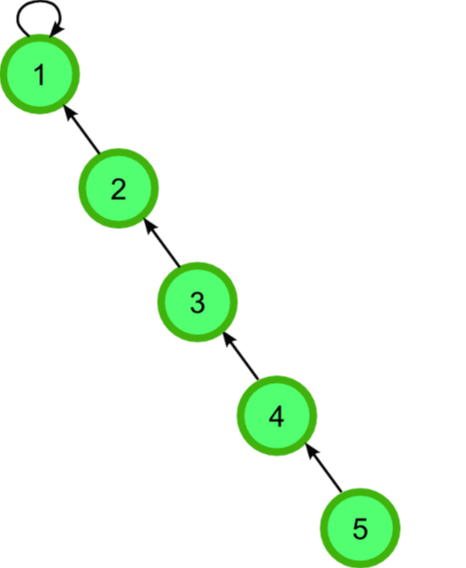
Alt text

우리는 여기서 한 가지 개선을 할 수 있다.

5번에서 1번 까지(5 - 4 - 3- 2 - 1)의 경로에 있는 모든 원소는 전부 루트를 1로 갖는다. 그렇다면 5번도 1을, 4번도 1을.. 2번도 1을 가리켜도 이 부분집합을 구성하는 원소는 변함이 없을 것이다. 이렇게 되면 아래 그림처럼 5번에서 2번까지 1번을 루트로서 바로 가리키게 되고 find(n) 연산 수행 시 시간 복잡도는 상수 시간 O(1)이 된다.

이것을 Path compression(경로 압축)이라 한다.

Union-Find with path compression:

Alt text

find(5) 연산 수행 시 5에서 루트 1로 가는 경로에 있는 모든 원소를 재귀 호출이나 For loop을 이용해서 1을 루트로 바로 가리키게 구현할 수 있다.

  1. x가 x의 부모와 같다면(자기 자신이 루트)라면 x를 반환한다.
  2. 다르다면 x의 부모는 x의 부모의 재귀 리턴 값이 된다.
  3. 재귀가 진행되면서 루트를 만나게 되면(매개변수로 들어온 값이 자기 자신 = 루트) x를 반환한다.
int find(x){
     if (parent[x] != x)
        parent[x] = find(parent[x]);
     return x;
}

Union by Rank

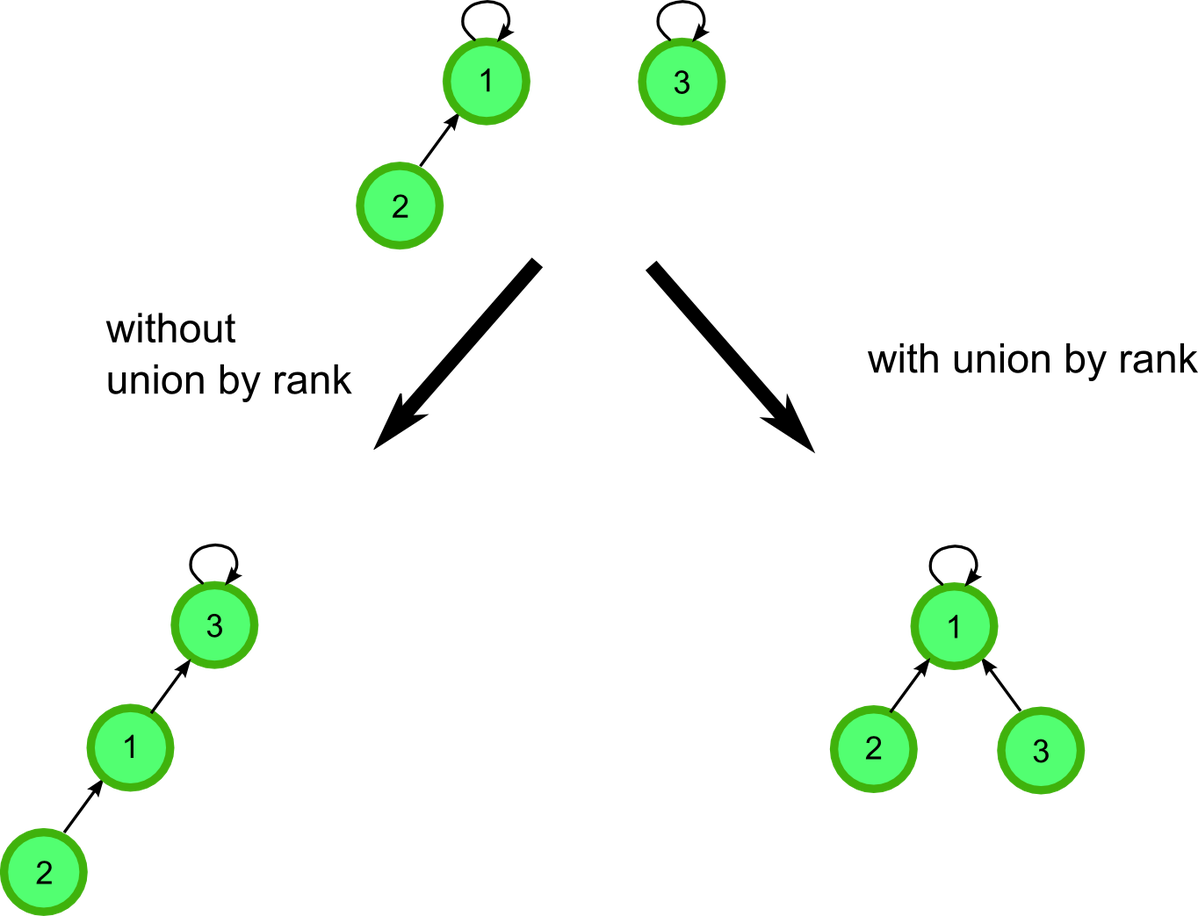
트리의 깊이 또는 높이는 유니온 파인드 연산 실행시간에 영향을 주는데 트리를 합칠 때 높이가 작은 트리를 높이가 큰 트리의 루트에 붙이면 높이가 높아지지 않는다. 이렇게 유니온 바이 랭크(union by rank)는 높이가 작은 트리를 큰 트리의 루트에 붙이는 방법이다.

※ 단, 높이가 같은 트리를 합칠 땐 높이가 +1 높아진다.

우리는 여기서 랭크라는 표현을 쓰는데, 트리의 높이는 위에서 살펴본 path compresstion에 의해서 줄어들 수 있고 업데이트 되지 않기 때문이다. 그래서 랭크라는 표현을 쓴다.

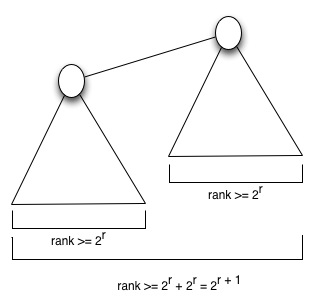
Alt text

어떤 원소 u가 한 트리의 루트이고 랭크 $r$을 가진다고 하면 유니온 바이 랭크 연산 하에 그 트리의 노드 수는 최소 $2^r$이 되고, 랭크 $r$로 같은 두 트리를 Union by rank 하면 랭크는 1 높아지게 되고 노드의 수는 $2^r + 2^r = 2^(r+1)$가 된다. 노드의 수는 2배가 되고 랭크는 1 높아지므로 연산 수행 시간이 $O(logn)$으로 보장이 된다.

Alt text

원소마다 랭크 정보를 유지하기 위해서 Make set의 for loop에 rank [i] = 0을 추가해 준다.

for (i=1; i<=n; i++){
    parent[i] = i;
    rank[i] = 0; // 처음에는 랭크가 전부 0
}

아래는 union by rank 코드이다.

  1. 두 원소의 루트를 구해서 서로 같다면 합치지 않고 유니온 연산을 종료한다.
  2. 그렇지 않다면, x의 루트랭크가 y의 루트랭크보다 크거나 같다면 y의 루트를 x의 루트 아래로 붙인다. (else 서로 스왑해서 수행)
  3. 두 트리의 랭크가 서로 같다면 랭크+1을 해준다. (두 트리의 랭크가 같으니 합치면 랭크가 +1 된다.)
void union(int x, int y)
     xRoot = find(x);
     yRoot = find(y);
     if xRoot == yRroot
         return
 
     if (rank[xRoot] >= rank[yRoot])
         parent[yRoot] = xRoot;
     else
         parent[xRoot] = yRoot;
 
     if (rank[xRoot] == rank[yRoot])
         rank[yRoot] = rank[xRroot] + 1

Application

유니온 파인드는 무향 그래프에서의 사이클 존재 유무를 판별할 때 사용될 수 있다. (단, 셀프 루프는 없어야 한다.)

또한, 크루스칼 알고리즘에서 최소 스패닝 트리를 찾는데에 자료구조로서 사용된다.

최소 스패닝 트리는 노드의 수가 n개 일 때 n-1개의 최소 비용의 간선으로 이루어진 트리로서, 그래프에서 최소비용의 간선을 선택하면서 만들어지는 트리에 사이클이 형성되지 않아야 하기에 사이클 형성 유무 판별에 유니온 파인드가 사용된다.

Link: 크루스칼 알고리즘 글 보러가기.

Union by Lank with Path Compression

class unionFind{
    private int parent[];
    private int rank[];
    private int n;
 
    unionFind(int cnt) {
        this.n = cnt;
        parent = new int[n];
        rank = new int[n];
    }
 
    public void makeSet() {
        for (int i = 0; i < n; i++) {
            parent[i] = i;
            rank[i] = 0;
        }
    }
 
    public int find(int x) {
        if (parent[x] == x)
            return x;
        else
            return parent[x] = find(parent[x]); // * 경로 압축
    }
 
    public void union(int root1, int root2) {
        root1 = find(root1);
        root2 = find(root2);
 
        if (root1 == root2) // 루트가 같다면 수행하지 않는다.
            return;
 
        if (rank[root1] >= rank[root2]) { // 루트1의 랭크가 루트2의 랭크보다 크다면
            parent[root2] = parent[root1]; //루트2가 루트1의 밑으로 합친다
        } else { // 위의 if문 과 반대
            parent[root1] = parent[root2];
        }
        if (rank[root1] == rank[root2])
            rank[root1]+=1;
    }
}

백준 온라인 저지에 있는 유니온 파인드 문제 1717번 집합의 표현 코드이다.

BOJ - 1717번

import java.io.BufferedReader;
import java.io.IOException;
import java.io.InputStreamReader;
import java.util.StringTokenizer;

public class Main {
    public static void main(String[] args) throws IOException {
        BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
        StringTokenizer st = new StringTokenizer(br.readLine());
        StringBuilder sb = new StringBuilder();
        int n = Integer.parseInt(st.nextToken());
        int m = Integer.parseInt(st.nextToken());
        unionFind h = new unionFind(n+1);
        h.makeSet();
        for (int i = 0; i < m; i++) {
            st = new StringTokenizer(br.readLine());
            int operation = Integer.parseInt(st.nextToken());
            int a = Integer.parseInt(st.nextToken());
            int b = Integer.parseInt(st.nextToken());
            if(operation == 0)
                h.union(a ,b);
            else
                sb = h.find(a) == h.find(b) ? 
                sb.append("YES").append("\n") : sb.append("NO").append("\n");
        }
        System.out.println(sb.toString());
    }
}

class unionFind {
    private int parent[];
    private int rank[];
    private int n;

    unionFind(int cnt) {
        this.n = cnt;
        parent = new int[n];
        rank = new int[n];
    }

    public void makeSet() {
        for (int i = 0; i < n; i++) {
            parent[i] = i;
            rank[i] = 0;
        }
    }

    public int find(int x) {
        if (parent[x] == x)
            return x;
        else
            return parent[x] = find(parent[x]); // * 경로 압축
    }

    public void union(int root1, int root2) {
        root1 = find(root1);
        root2 = find(root2);

        if (root1 == root2) // 루트가 같다면 수행하지 않는다.
            return;

        if (rank[root1] >= rank[root2]) { // 루트1의 랭크가 루트2의 랭크보다 크다면
            parent[root2] = parent[root1]; //루트2가 루트1의 밑으로 합친다
        } else { // 위의 if문 과 반대
            parent[root1] = parent[root2];
        }
        if (rank[root1] == rank[root2])
            rank[root1]+=1;
    }
}

References

Leave a comment

You may also enjoy