Gyeong

Gyeong

It is in the moment of decisions that your destiny is shaped.

들어가기 전에: 크루스칼 알고리즘에는 다음의 선행지식이 필요합니다.

크루스칼 알고리즘(Kruskal’s Algorithm)

크루스칼 알고리즘(Kruskal’s Algorithm)은 연결 가중치 그래프(connected weighted graph)에서 최소 스패닝 트리(Minimum spanning tree)를 찾는 알고리즘이다. 알고리즘 과정에서 볼 때 그래프의 숲(forest)관점에서 여러개의 트리 중 서로 다른 집합의 두 트리를 연결하는 가능한 최소 가중치 간선(least possible weighted edge)을 찾는 작업을 수행한다.

그래프 이론에서는 그리디 알고리즘의 하나로서 알고리즘의 매 과정마다 최소 가중치 간선을 하나씩 선택해 추가하는 작업을 하면서 연결 가중치 그래프에서 최소 스패닝 트리를 찾는다. 그리하여 모든 정점을 포함하고 간선들의 서브셋인 스패닝 트리를 형성하게 하고, 생성된 스패닝 트리의 모든 간선의 가중치 합을 최소로 만든다.

그래프가 연결 그래프가 아니라면, 크루스칼 알고리즘은 최소 스패닝 숲(Minimum spanning forest)을 찾는다. (비 연결 그래프 내의 각 연결된 그래프에서의 최소 스패닝 트리)

알고리즘

크루스칼 알고리즘이 어떻게 동작하는지 살펴보자.

그래프 G가 주어졌다고 하자. (여기서는, 비 연결 그래프, 연결 그래프 구분하지 않는다.)

  • 그래프 G의 모든 정점이 분리된 트리들의 집합인 숲(Forest) F를 생성한다.
    여기서 숲은 분리된 트리들의 집합이다. (a set of trees)

  • 그래프 G의 모든 간선을 포함하는 집합 S를 생성한다.

  • While 집합 S가 공집합이 아니고 && 숲 F가 스패닝 트리가 아니면

    • 집합 S에서 가장 최소 가중치의 간선을 하나 선택하고 S로 부터 삭제한다.
    • 선택된 간선이 서로 다른 두 트리를 연결한다면 숲 F에 선택된 간선을 추가한다.
      이것은 두 트리를 하나의 트리로 합치는 것이다.

알고리즘이 끝나고, 그래프 G가 비 연결 그래프 였다면 숲 F는 다중 컴포넌트(Trees)의 최소 스패닝 숲(MSF)을 형성하고, 그래프 G가 연결 그래프 였다면 숲 F는 단일 컴포넌트의 최소 스패닝 트리(MST)를 형성하게 된다.

다음은 크루스칼 알고리즘의 Animation이다.

Alt

  • 파란색 간선은 현재 집합 S에서 선택한 간선
  • 빨간색 간선은 집합 S에서 선택한 간선을 숲 F에 추가한 간선이다.

사이클을 형성하지 않으면서 간선들을 하나씩 추가하며 정점의 개수가 V라면 V-1개의 간선을 가진 최소 스패닝 트리를 구성하고 있는 모습이다.

의사코드

다음은 크루스칼 알고리즘의 의사코드이다. (Union Find 자료구조 사용)

Warning: 의사코드에는 Union Find - 서로소 집합 자료구조가 사용이 되므로 모른다면 반드시 알고와야 이해가 가능하다.

algorithm Kruskal(G) is
    // 공집합으로 초기화
    A := ∅
    // 그래프 G의 모든 정점에 대해서
    for each v ∈ G.V do
        // 모든 정점들을 하나의 독립된 트리로 만들어 준다.
        MAKE-SET(v)
    // 그래프 G의 모든 간선들에 대해서 (간선들은 전부 오름차순으로 나열 되어있다.)
    for each (u, v) in G.E ordered by weight(u, v), increasing do
        // u와 v가 속한 집합이 서로 다르면 (서로 다른 집합의 트리라면)
        if FIND-SET(u) ≠ FIND-SET(v) then
           // u, v를 정점으로 하는 간선 (u, v)를 집합 A에 포함 시킨다.
           A := A ∪ {(u, v)}
           // 두 집합 u, v를 하나의 집합으로 합친다.
           UNION(FIND-SET(u), FIND-SET(v))
    return A

예제

예를 들어 크루스칼 알고리즘이 어떻게 동작하는지 하나씩 알아보자.

다음의 그래프에서 크루스칼 알고리즘을 적용해 최소 스패닝 트리를 찾아본다.

Graph G:

Alt

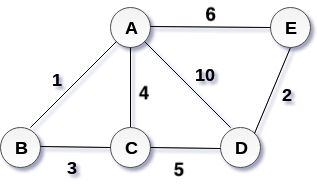
다음은 위 그래프의 가중치 간선들의 정보이다.

Edge	AE   AD   AC   AB   BC   CD   DE
Weight	6    10   4    1    3    5    2

먼저, 간선들을 가중치에 따라 오름차순으로 정렬한다.

Edge	AB   DE   BC   AC   CD   AE   AD
Weight	1    2    3    4    5    6    10

MST 구축을 시작한다.

위 간선 집합에서 가중치가 1로 제일 작은 최소 가중치 간선인 AB를 선택한다.
정점 A와 정점B는 서로 다른 집합이므로 간선 AB를 MST에 추가한다.

MST: Alt

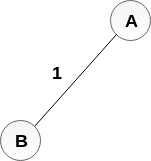
이번에는 AB를 선택했으니 그 다음으로 가중치가 작은 간선을 선택한다. 여기서는 가중치가 2인 간선 DE를 선택한다.

정점D와 정점E는 서로 다른 집합이므로 간선 DE를 MST에 추가한다.

MST: Alt

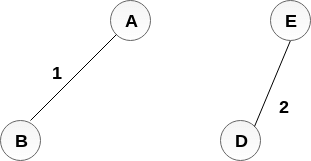
계속해서, DE를 선택했으니 그 다음으로 가중치가 작은 간선을 선택한다. 여기서는 가중치가 3인 간선 BC를 선택한다.

정점B와 정점C는 서로 다른 집합이므로 간선 BC를 MST에 추가한다.

MST: Alt

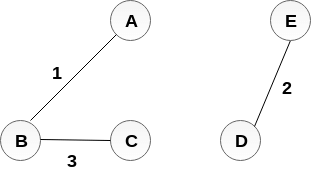
계속해서, BC를 선택했으니 그 다음으로 가중치가 작은 간선을 선택한다. 여기서는 가중치가 4인 간선 AC를 선택한다.

그러나 정점A와 정점C는 서로 이미 같은 집합에 속해 있다. 따라서 간선 AC를 추가하면 사이클이 생긴다는 것을 알 수 있다.

MST: Alt

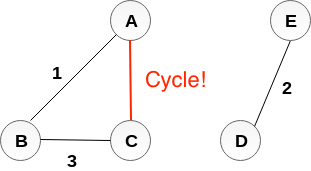
MST는 트리이므로 사이클이 없어야 한다는 것을 알고있다. 따라서, 간선 AC는 버린다.

계속해서, 간선 AC 다음으로 가중치가 작은 간선을 선택한다. 여기서는 가중치가 5인 간선 CD를 선택한다.

정점C와 정점D는 서로 다른 집합이므로 해당 정점들을 끝점으로 하는 간선을 추가해도 사이클을 형성하지 않는다. 간선 CD를 MST에 추가한다.

MST: Alt

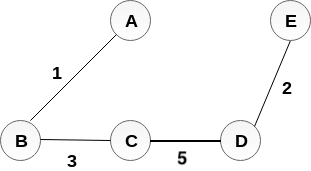
이로서 그래프 G의 모든 정점을 포함하고 4개(V-1)의 간선으로 구성되는 최소 스패닝 트리(MST)가 완성이 되었다.

위 트리의 모든 간선의 가중치 합은 11로서 그래프 G에서 나올 수 있는 스패닝 트리 중 가장 작은 가중치의 합을 가진 스패닝 트리가 된다.

구현

다음은 유니온 파인드 자료구조를 이용하여 크루스칼 알고리즘을 구현한 C++ 코드이다.

그래프는 위의 예제를 이용하였다.

예제 입력은 다음과 같다.

  • 그래프의 정점의 수와 간선의 수를 입력한다.
    nodes, edges
  • 그 다음 그래프의 각 간선별 정보를 입력한다.
    x, y, weight

결과 출력은 다음과 같다.

  • 해당 그래프의 MST 간선 가중치 총합을 출력한다.
    Minimum cost is ?

Kruskal’s algorithm - C++ Code

#include <iostream>
#include <vector>
#include <utility>
#include <algorithm>
using namespace std;
const int MAX = 1e4 + 5;
int id[MAX], ranks[MAX], nodes, edges;

// Edge array : weight, (u, v)
pair <long long, pair<int, int> > p[MAX];

// Make set initialization
void init()
{
    for(int i = 0;i < MAX;++i) {
        id[i] = i;
        ranks[i] = 0;
    }
}

// Find with path compression
int root(int x)
{
    if (id[x] == x)
        return x;
    else
        // Recursion
        return id[x] = root(id[x]);
}

// union by rank
void union1(int x, int y)
{
    int p = root(x);
    int q = root(y);

    if (p == q) // 루트가 같다면 수행하지 않는다.
        return;

    // p의 랭크가 q의 랭크보다 크다면
    if (ranks[p] >= ranks[q]) {
        // q가 p의 밑으로 되게 합친다.
        id[q] = id[p];
    } else { // 위의 if문 과 반대
        id[p] = id[q];
    }
    // 두 트리의 랭크가 같다면, 랭크를 1만큼 키운다.
    if (ranks[p] == ranks[q])
        ranks[p]+=1;
}

// Find MST
long long kruskal(pair<long long, pair<int, int> > p[])
{
    int x, y;
    int cnt = 0;
    long long cost, minimumCost = 0;
    for(int i = 0; i < edges; ++i)
    {
        x = p[i].second.first;
        y = p[i].second.second;
        cost = p[i].first;
        if(root(x) != root(y))
        {
            minimumCost += cost;
            union1(x, y);
            cnt++;
        }
        if (nodes-1 == cnt)
            break;
    }
    return minimumCost;
}

int main()
{
    int x, y;
    long long weight, minimumCost;
    init();
    cout <<"Enter Nodes and edges";
    cin >> nodes >> edges;
    for(int i = 0;i < edges;++i)
    {
        cout<<"Enter the value of X, Y and edges";
        cin >> x >> y >> weight;
        p[i] = make_pair(weight, make_pair(x, y));
    }
    sort(p, p + edges);
    minimumCost = kruskal(p);
    cout <<"Minimum cost is "<< minimumCost << endl;
    return 0;
}

Output

Enter Nodes and edges 5 7
Enter the value of X, Y and edges 1 2 1
Enter the value of X, Y and edges 2 3 3
Enter the value of X, Y and edges 1 3 4
Enter the value of X, Y and edges 1 5 6
Enter the value of X, Y and edges 3 4 5
Enter the value of X, Y and edges 1 4 10
Enter the value of X, Y and edges 4 5 2
Minimum cost is 11

References

Kruskal’s Algorithm - java T point
Kruskal’s Algorithm

Leave a comment

You may also enjoy