스패닝 트리와 최소 스패닝 트리(Minimum Spanning Tree)

들어가기 전에: 먼저 스패닝 트리가 무엇인지 알아보자.

스패닝 트리(Spanning tree)

G: 그래프
T: 스패닝 트리
V: 모든 정점의 개수
E: 모든 간선의 개수

라고 하자.

그래프 이론에서 어떤 비방향 그래프 G가 있다고 하면, 그 비방향 그래프 G의 스패닝 트리 T는 이렇게 정의된다.

Definition

그래프 G의 모든 정점을 연결하면서 가능한 최소의 간선 개수로 이루어지는 트리(또는 서브 그래프). (트리이므로 사이클은 포함하지 않아야 한다.)

이에 따라, 그래프 G의 스패닝 트리 T는 그래프 G의 모든 정점의 수 V개를 가지며, 간선의 개수는 V-1개를 가진다.

트리란?: 여기서 트리는 사이클을 가지지 않는 비방향 연결 그래프를 말한다.

아래 그림은 그래프 G의 스패닝 트리 T를 나타낸 것이다.

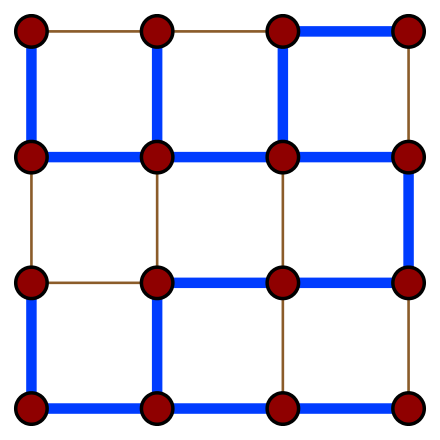
빨간점은 스패닝 트리 T의 정점, 파란선은 스패닝 트리 T의 간선을 나타낸다.

그림에서 보이는 것과 같이 스패닝 트리 T는 그래프 G의 모든 정점을 연결하고 있고, 스패닝 트리 T를 구성하는 간선의 개수는 최소가 되고 있다. 또한 사이클을 포함하지 않는다.

위 그래프 G의 정점의 개수를 V개라 하면, 스패닝 트리 T는 정점의 개수가 V개 즉, 16개 간선의 수는 V-1개 즉, 15개로 이루어져 있다.

일반적으로, 그래프는 아래 그림처럼 여러개의 스패닝 트리를 가질 수 있다.

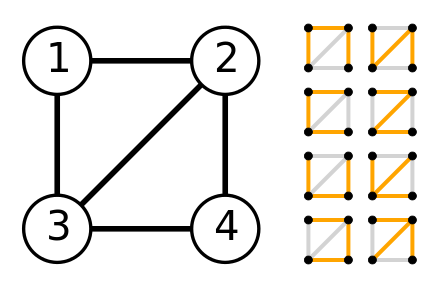
하지만 그래프 G가 연결 그래프가 아니라면 스패닝 트리를 가질 수 없다.

만약 그래프 G의 모든 간선이 그래프 G의 스패닝 트리 T의 간선과 동일하다면, 그래프 G는 트리이고 또한 스패닝 트리 T라고 할 수 있다. (이것은 그래프 G가 유일한 스패닝 트리를 가질 수 있음을 의미한다.)

그래프 G의 스패닝 트리는 이렇게도 정의 될 수 있다.

사이클을 포함하지 않는 그래프 G의 간선의 최대 집합 혹은 그래프 G의 모든 정점을 연결하는 그래프 G의 간선의 최소 집합.

Fundamental cycles

스패닝 트리를 포함하는 그래프G의 간선들 중에서 스패닝 트리를 구성하지 않는 간선을 하나만 추가하면 사이클이 생긴다. 이러한 사이클을 Fundamental cycles이라 부른다.

스패닝 트리에 포함되지 않는 그래프의 각 간선들 마다 고유한 Fundamental cycles이 존재한다. 따라서, 스패닝 트리에 포함되지 않는 그래프의 각 간선들과 Fundamental cycles은 1:1 관계라고 볼 수 있다.

정점 V개의 연결 그래프는 V-1개의 간선을 가진 스패닝 트리를 가질 것이고 이는, 간선의 개수가 E개의 연결 그래프의 어떤 한 스패닝 트리는 E-V+1개의 Fundamental cycles을 가지게 된다.

요약: V: 그래프 G의 정점 개수, E: 그래프 G의 간선 개수라 한다면
스패닝 트리에 포함되지 않는 그래프 G의 간선들 = E - (V-1) = E - V + 1.
Fundamental cycles과 스패닝 트리에 포함되지 않는 그래프 G의 간선들은 1:1 관계이므로
Fundamental cycles = E - V + 1.

Fundamental cut sets

연결된 그래프 G에서, 그래프 G를 이루는 간선들 중 어느 간선들의 삭제가 그래프 G를 비연결 그래프로 만들게하는데 그 간선들의 집합을 cut sets이라 한다. cut sets은 그래프 G를 항상 두개의 그래프로 나눈다.

아래 그림은 그래프 G의 cut sets을 보여준다.

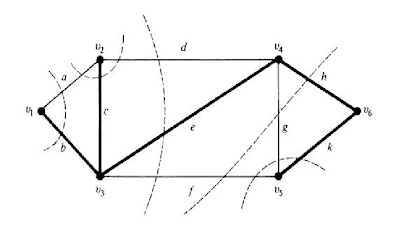
스패닝 트리는 그 트리를 이루는 간선들 중 하나의 간선만 삭제하면, 스패닝 트리를 이루는 정점들은 서로 다른 두개의 정점들 집합으로 분리된다. 따라서, 스패닝 트리를 이루는 모든 간선들은 cut sets이라고 볼 수 있다.

이러한, 스패닝 트리의 하나의 간선(가지)만을 포함하는 cut sets을 Fundamental cut sets이라고 한다.

최소 스패닝 트리(Minimum spanning tree)

위의 스패닝 트리를 이해했다면 최소 스패닝 트리의 개념은 간단하다.

그래프 G의 스패닝 트리 중에서 그 스패닝 트리를 구성하는 간선들의 가중치의 합이 최소가 되는 트리를 최소 스패닝 트리라고 한다.

다음 그래프 G의 그림을 보자.

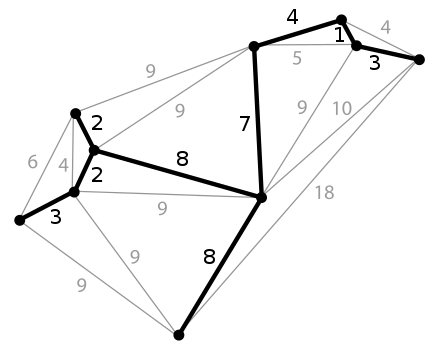
굵은 검은선과 검은 정점들은 그래프G 최소 스패닝 트리를 나타내고, 회색 실선은 스패닝 트리에 포함되지 않는 그래프의 간선들을 나타낸다.

이처럼, 위 그림에서의 스패닝 트리는 여러가지가 있겠지만, 위 그림에서 표시된 스패닝 트리가 간선들의 가중치 합이 최소가 되게 하고 있다. (간선과 가중치의 구성에 따라 여러개의 최소 스패닝 트리가 나올 수 있다.)

컴퓨터 과학에서 이러한 그래프가 주어지면 최소 스패닝 트리를 구하는 알고리즘은 대표적으로 프림 알고리즘, 크루스칼 알고리즘 두 가지가 있다.

References

---

Spanning Tree - Wikipedia
Cut sets