Gyeong

Gyeong

It is in the moment of decisions that your destiny is shaped.

이분 탐색(Binary Search)

컴퓨터 과학(Computer science)에서 이분 탐색(Binary Search)은 정렬된 배열(Sorted array)에서 찾고자 하는 값의 존재 유무나 위치를 찾는 알고리즘이다. 이분 탐색은 찾고자 하는 값을 배열의 중간 원소와 비교한다. 두 개의 값이 같지 않다면, 찾고자 하는 값이 놓여있지 않다고 판단되는 배열의 반은 탐색 범위에서 제외되고 나머지 반을 다시 탐색한다. 이것을 찾고자 하는 값이 나올 때까지 반복하는데, 탐색 공간이 빈 공간(크기가 0)이 되어 탐색이 끝나게 되면 해당 배열에서 찾고자 하는 값이 없다는 것을 의미한다.

탐색을 수행할 배열의 원소 개수가 $n$개일 때 이분 탐색은 복잡도 면에서 최악의 경우 $O(logn)$의 로그적 시간에 동작한다. 앞에서 부터 순서대로 하나씩 탐색하는 순차 혹은 선형 탐색(linear search)과 비교하면 작은 크기의 배열을 제외할 시 이분 탐색이 더 빠르다고 할 수 있다. 순차 탐색은 탐색에 있어 배열의 원소 순서에 제약이 없지만 이분 탐색은 원소의 정렬이 완료된 배열에서 탐색이 가능하다.

Algorithm

가장 일반적인 알고리즘을 보자.

배열은 오름차순으로 정렬되어 있다고 가정하고 시작한다. 먼저 찾고자 하는 값을 배열의 중간 위치의 원소 값과 비교한다. 찾고자 하는 값이 중간 위치의 원소 값과 일치하면 그 중간 원소의 위치를 반환하고 알고리즘을 끝낸다. 찾고자 하는 값이 중간 원소의 값보다 작다면 중간 원소를 기준으로 오른쪽의 값들은 찾고자 하는 값들보다 크므로 탐색을 수행할 필요가 없다. 따라서 왼쪽 반에 대해서 이분 탐색을 수행한다. 찾고자 하는 값이 중간 원소의 값보다 그다면 중간 원소를 기준으로 왼쪽의 값들은 찾고자 하는 값들보다 작으므로 탐색을 수행할 필요가 없다. 따라서 오른쪽 반에 대해서 이분 탐색을 수행한다. 이것을 원하는 값을 찾을 때 까지 수행한다. 탐색을 수행하다가 탐색 범위의 크기가 0이 되면 배열에서 찾고자 하는 값이 없다는 것을 의미한다.

Procedure

$n$개의 원소로 이루어진 $A_0,A_1,A_2,…,A_{n-1}$ 배열 $A$가 주어지고 원소들은 오름차순 $A_0 \leq A_1 \leq A_2 \leq … \leq A_{n-1}$ 으로 정렬되어 있다. 그리고 찾고자 하는 값 $T$가 주어진다.

다음의 절차로 배열 $A$에서 값 $T$를 찾는다.

  1. 배열의 맨 처음 인덱스를 가리키는 $L$을 $0$으로 배열의 맨 끝 인덱스를 가리키는 $R$을 $n-1$로 놓는다.

  2. $L \gt R$ 이면 탐색 공간의 크기가 0이 되고 배열에서 찾고자 하는 값이 없다는 것을 의미하므로 알고리즘을 종료한다.

  3. 배열의 중간 인덱스 원소를 가리키는 $m$을 $\lfloor\frac{L + R}{2}\rfloor$로 놓는다. $\lfloor x \rfloor$, floor 기호는 $x$ 값 보다 크거나 같은 수 중 가장 작은 정수를 의미한다. 예) $\lfloor\frac{1+2}{2}\rfloor$ = 1이다.

  4. $A_m \lt T$이면 $L$을 $m+1$로 놓고 2번으로 간다.

  5. $A_m \gt T$이면 $R$을 $m-1$로 놓고 2번으로 간다.

  6. $A_m = T$ 이면 $m$을 반환하고 알고리즘을 종료한다.

다음은 위 절차에 대한 의사코드이다.

function binary_search(A, n, T) is
    L := 0
    R := n − 1
    while L ≤ R do
        m := floor((L + R) / 2)
        if A[m] < T then
            L := m + 1
        else if A[m] > T then
            R := m - 1
        else:
            return m
    return unsuccessful

Alternative procedure

위에서 알아본 방법에서는 탐색의 매 반복 마다 중간 값 원소와 $T$를 비교하는 구문이 있다면, 이번 방법에서는 $L = R$이 같을 때에만 값이 같은지 체크를 수행한다. 이 방법은 위의 방법에 비해 비교 구문을 하나 제거하였기에 루프에서 빠른 비교를 가능하게 하지만 평균 상황에서 한 번의 반복을 더 요구한다.

다음의 절차로 배열 $A$에서 값 $T$를 찾는다.

  1. 배열의 맨 처음 인덱스를 가리키는 $L$을 $0$으로 배열의 맨 끝 인덱스를 가리키는 $R$을 $n-1$으로 놓는다.

  2. while $L \neq R$

    1. 배열의 중간 인덱스 원소를 가리키는 $m$을 $\lceil\frac{L + R}{2}\rceil$로 놓는다. $\lceil x \rceil$, ceil 기호는 $x$ 값 보다 크거나 같은 수 중 가장 작은 정수를 의미한다. 예) $\lceil\frac{1+2}{2}\rceil$ = 2이다.

    2. $A_m \gt T$이면 $R$을 $m-1$로 놓는다.

    3. $A_m \leq T$이면 $L$을 $m$으로 놓는다.

  3. 이제 $L = R$ 이다. $A_L = T$ 이면 $L$을 반환한다. 아니라면, unsuccessful을 반환한다.

다음은 위 절차에 대한 의사코드이다.

function binary_search_alternative(A, n, T) is
    L := 0
    R := n − 1
    while L != R do
        m := ceil((L + R) / 2)
        if A[m] > T then
            R := m - 1
        else:
            L := m
    if A[L] = T then
        return L
    return unsuccessful

Duplicate elements

앞에서 알아본 방법에 의해 이분 탐색은 배열에서 찾고자 하는 값의 위치를 반환하는데, 중복된 값이 존재해도 마찬가지로 동작한다. 정렬된 배열 $[1,2,3,4,4,5,6,7]$이 있고 찾고자 하는 값이 4일 때, 위에서 알아본 방법에 의해 각각 4번째 위치(3번 인덱스)와 5번째 위치(4번 인덱스)를 반환할 것이다. 처음 알아본 방법은 4번째 위치를 반환할 것이다. 하지만 처음 알아본 방법은 중복된 값이 있으면 그 중에서 제일 처음 값을 반환하지 않는데, 만약 배열 $[1,2,4,4,4,5,6,7]$이 있다고 하면 처음 방법은 4번째 값을 반환하고, 중복된 첫번째 값(3번째 위치)을 반환하지 않는다. 특정 문제나 상황에서 배열에 찾고자 하는 값의 중복된 값이 존재하고 그 값들 중 가장 왼쪽 값 또는 가장 오른쪽 값을 찾아야 하는 경우가 있다. 배열 $[1,2,4,4,4,5,6,7]$에서 값 4의 가장 왼쪽 값은 3번째 위치의 4이고, 가장 오른쪽 값은 5번째 위치의 4이다. 위에서 알아본 Alternative procedure는 배열에서 찾고자 하는 값이 존재하면, 찾고자 하는 값들 중 가장 왼쪽의 위치를 반환한다.

Procedure for finding the leftmost element

다음은 중복된 값들 중 가장 왼쪽에 있는 값을 찾는 알고리즘이다.

  1. 배열의 맨 처음 인덱스를 가리키는 $L$을 $0$으로 배열의 맨 끝 인덱스를 가리키는 $R$을 $n$으로 놓는다.

  2. while $L \lt R$

    1. 배열의 중간 인덱스 원소를 가리키는 $m$을 $\lfloor\frac{L + R}{2}\rfloor$로 놓는다.

    2. $A_m \lt T$이면 $L$을 $m+1$로 놓는다.

    3. $A_m \geq T$이면 $R$을 $m$으로 놓는다.

  3. $L$을 반환한다.

위의 과정을 거치고, $L \lt n$ $and$ $A_L = T$ 이면 $A_L$은 $T$와 같은 가장 왼쪽에 있는 원소이다. $T$가 배열에 있다면 $L$은 $T$의 가장 왼쪽 원소 위치를 가리키는 동시에 $T$보다 작은 원소들의 개수를 의미한다. 이것을 $Rank$라고 한다. $T$가 배열에 없다면 $L$은 $T$보다 작은 원소들의 개수를 의미한다.

다음은 위 알고리즘의 의사코드이다.

function binary_search_leftmost(A, n, T):
    L := 0
    R := n
    while L < R:
        m := floor((L + R) / 2)
        if A[m] < T:
            L := m + 1
        else:
            R := m
    return L

Procedure for finding the rightmost element

다음은 중복된 값들 중 가장 오른쪽에 있는 값을 찾는 알고리즘이다.

  1. 배열의 맨 처음 인덱스를 가리키는 $L$을 $0$으로 배열의 맨 끝 인덱스를 가리키는 $R$을 $n$으로 놓는다.

  2. while $L \lt R$

    1. 배열의 중간 인덱스 원소를 가리키는 $m$을 $\lfloor\frac{L + R}{2}\rfloor$로 놓는다.

    2. $A_m \gt T$이면 $R$을 $m$으로 놓는다.

    3. $A_m \leq T$이면 $L$을 $m+1$로 놓는다.

  3. $R-1$을 반환한다.

위의 과정을 거치고, $R \gt 0$ $and$ $A_{R-1} = T$ 이면 $A_{R-1}$은 $T$와 같은 가장 오른쪽에 있는 원소이다. $T$가 배열에 있다면 $R-1$은 $T$의 위치를 가리킨다. $n-L$은 $T$ 보다 작은 원소들의 개수를 의미한다.

다음은 위 알고리즘의 의사코드이다.

function binary_search_rightmost(A, n, T):
    L := 0
    R := n
    while L < R:
        m := floor((L + R) / 2)
        if A[m] > T:
            R := m
        else:
            L := m + 1
    return R - 1

Approximate matches

이분 탐색은 배열에서 찾고자 하는 값의 위치를 알아낼 때도 쓸 수 있지만, 정렬된 배열에서 동작하는 알고리즘 특성 상 배열에 해당 값이 없어도 그 값과 대략적으로 일치하는 값의 위치를 알아내는 데에도 적용할 수 있다.

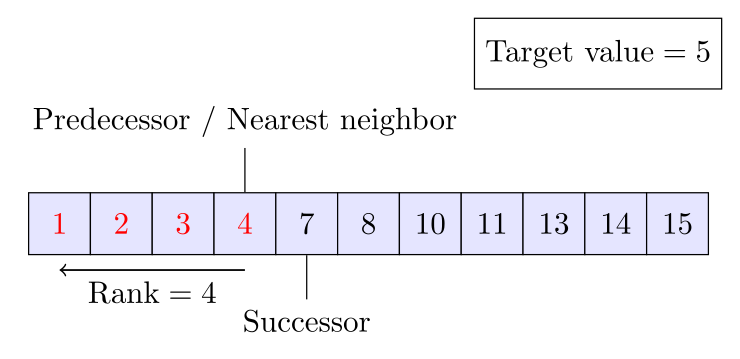
Alt text

위 그림에서 보이듯이, 이분 탐색을 활용하면 Target value의 Rank, predcessor, successor, nearest neighbor를 계산할 수 있다. 또한 특정 두 원소 사이에 몇 개의 원소가 있는지 찾는 범위 질의(Range queries)도 두 값의 $Rank$를 안다면 쉽게 계산 할 수 있다.

  • Rank queries: Target value 보다 작은 원소의 개수를 위에서 $Rank$라고 했었다. $Rank$는 위에서 알아본 procedure for finding the leftmost element를 이용하여 알아낼 수 있다. 이 procedure에서는 Target value 보다 작은 원소의 개수를 의미하는 $L$을 반환한다.

  • predcessor queries: 선행자 - predcessor는 바로 위에서 알아본 Rank queries에서 알아낼 수 있다. target value의 $rank$가 $r$이라고 하면 predcessor는 $r-1$이 된다.

  • successor queries: 후행자 - successor는 procedure for finding the rightmost element를 통해 알아낼 수 있다. 이 procedure가 반환한 값이 $r$이라면 successor는 $r+1$이 된다.

  • nearest neighbor: predcessor와 successor 중 더 가까운 쪽이 nearest neighbor가 된다.

  • Range queries: 두 값의 $Rank$를 안다면 첫번째 값 보다 크거나 같고 두번째 값보다 작은 원소의 개수는 두 $Rank$의 값의 차이이다. 이 개수는 범위의 끝점이 개수로 카운팅 되어야 하는가와 배열에서 해당 범위의 끝점이 target value와 일치 하는가에 따라 하나씩 증가 또는 감소할 수 있다.

Avoid integer overflow

C++이나 java와 같은 프로그래밍 언어에서는 Signed int가 4bytes의 공간을 차지한다. 이는 정수 값으로 -2147483648$(2^{31})$ ~ 2147483647$(2^{31}-1)$의 값을 표현 할 수 있다.

문제는 중간 원소의 위치를 계산하는 과정에서 $L + R$을 할 때 Interger의 범위를 넘을 수가 있다.

  • (L + R)/2 > 2147483647

Integer overflow를 피하기 위해서는 다음의 트릭을 쓸 수 있다.

  • L + (R - L)/2 또는 R - (R - L)/2

R-L을 함으로써 overflow를 피하고 이를 반으로 나누면 양 끝점에서 부터 중간 원소 까지의 떨어진 거리 Offset이 된다. 이를 맨 처음 인덱스에 더하거나, 맨 끝 인덱스에서 빼면 중간 원소의 위치가 계산된다.

이 트릭은 중간 위치를 정확하게 계산하면서 Integer 범위 안의 매우 큰 값에 대해서도 두 정수를 더할 때 Integer overflow를 방지한다.

performance

비교 횟수와 관련해, 이분 탐색의 성능은 이분 탐색이 만드는 이진 트리에서의 프로시저의 실행을 통해 분석할 수 있다. 트리의 루트 원소는 배열에서의 중간 위치의 원소이다. 배열의 중간 위치 원소를 기준으로 왼쪽 반은 루트 노드의 왼쪽 자식 트리이고, 오른쪽 반은 루트 노드의 오른쪽 자식 트리이다. 그 밑의 자식 트리들도 이와 같이 만들어 진다. 루트 노드를 시작으로 찾고자 하는 값과의 대소 비교를 통해 어느쪽 자식을 탐색할지 정해진다.

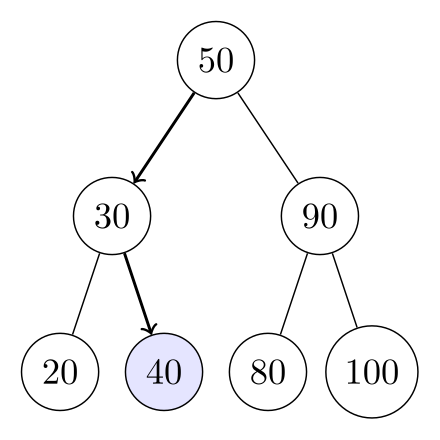
Alt text

위의 그림은 배열이 [20, 30, 40, 50, 80, 90, 100]일 때, 이분 검색이 그리는 트리를 나타내고 있다.
Target value가 40일 때, 그림처럼 루트 노드에서부터 비교를 시작해서 50, 30, 40순으로 탐색을 한다.

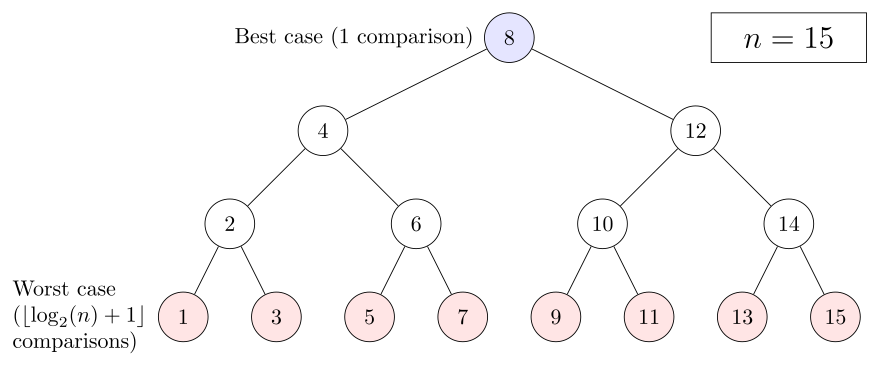
Alt text

시간적인 측면에서 보면 이분 검색은 최악의 경우, 찾고자 하는 값이 배열에 있을 때, 비교 반복 횟수를 $\lfloor log_2(n) + 1 \rfloor$번 만든다. 최악의 경우 찾고자 하는 원소가 트리의 가장 깊은 곳에 있어 $\lfloor log_2(n) + 1 \rfloor$만큼의 비교 검색을 수행해야 하기 때문이다.

찾고자 하는 값이 배열에 없을 때도 최악의 경우가 있을 수 있는데, n이 2의 제곱 수 이거나 탐색이 트리의 가장 깊은 곳에서 끝나면 비교 반복 횟수는 $\lfloor log_2(n) + 1 \rfloor$이 된다. 그렇지 않고, 탐색이 두번째로 가장 깊은 곳에서 끝나면 비교 반복 횟수는 1 줄어든 $\lfloor log_2(n)\rfloor$이 된다.

평균적인 상황에서는 모든 원소가 동일하게 검색될 가능성이 있다고 가정하면, 이분 탐색은 $\lfloor log_2(n) \rfloor + 1 - (2^{\lfloor log_2(n) + 1 \rfloor} - \lfloor log_2(n) -2 \rfloor)/n$의 비교 반복 횟수를 만든다. 이 값은 n이 커질 수록 대략적으로 $\lfloor log_2(n) - 1 \rfloor$ 값에 근접해진다.

최선의 상황에서는 찾고자 하는 값이 배열의 중앙에 있어 한번 만에 찾는 경우이다. 이는 한번의 비교 반복 횟수 만으로 원소를 반환하는 경우이다. - $O(1)$

공간적인 측면에서 보면 이분 탐색을 반복적인 방법으로 구현했을 시, 약간의 포인터 혹은 변수들은 $O(1)$의 공간을 요구한다. 또한 처음 프로그램이 호출될 때 단일 콜 스택 $O(1)$의 공간을 요구한다. 반복적인 방법은 다른 변수나 추가적인 Recursive call을 만들지 않기 때문에 전체적으로 $O(1)$의 공간만을 요구한다.

재귀적인 방법으로 구현할 시, 탐색의 매 단계마다 재귀 호출을 하는데, 이는 지금의 함수 호출 정보를 담은 스택 프레임(Stack frame)을 콜 스택(Call stack)에 저장하고 다시 재귀 호출을 한다는 것을 의미한다. 이분 탐색의 레벨 깊이가 m일 때 최악의 경우 m개의 스택 프레임이 만들어지므로 공간 복잡도는 이 레벨 깊이에 비례한다. 원소의 개수가 $n$개일 때 최대 레벨은 $\lfloor log_2n \rfloor + 1$개가 되므로 전체적으로 최악 $O(log_2n$)의 공간복잡도가 된다.

Time & Space Complexity

  • Worst Case performance: $O(log_2n)$

  • Average Case performance: $O(log_2n)$

  • Best Case performance: $O(1)$

  • Worst Case Space Complexity: Iterative: $O(1)$, Recursive: $O(log_2n)$ due to call stack

References

Leave a comment

You may also enjoy