트리(Tree)
트리는 부모와 자식간의 관계가 계층적으로 구성되는 자료구조이다.
하나의 노드가 여러개의 자식들을, 다시 자식들은 다른 자식들을 가질 수 있는 구조이다.
다음 그림은 전형적인 트리를 보여준다.
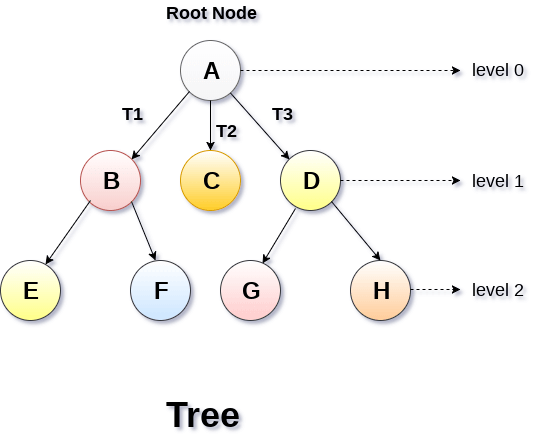
트리 용어
트리에 쓰이는 용어들을 알아보자.
루트(Root)
트리의 계층적 구조상 가장 위에 위치한 노드를 지칭한다.
위의 그림에서 A가 루트이다.
루트는 유일하게 부모 노드가 없는 노드이다.
리프 노드(Reaf Node)
아무런 자식도 가지지 않는 노드를 리프 노드라고 한다.
위의 그림에서 E, F, C, G, H가 리프 노드이다.
조상 노드(Ancestor)
특정 노드에서 루트로의 선행자가 이에 해당한다.
노드 F의 조상 노드는 B, A가 된다.
형제 노드(Sibling)
같은 부모를 가지는 노드들을 형제 노드라고 한다.
위의 그림에서 B, C, D가 형제 노드이다.
서브 트리(Sub Tree)
위의 그림에서 A가 null이 아니면, 그 밑의 자식 트리 T1, T2, T3를 노드 A의 서브 트리라고 한다.
레벨(Level)
트리는 계층적 구조로서 레벨을 가지고 있다.
루트는 0레벨이며, 밑 자식으로 갈수록 레벨이 1씩 커진다.
이진 트리
한 노드가 최대 2개의 자식 노드를 가질 수 있는 트리를 이진 트리라고 한다.
한 노드의 왼쪽에 오는 자식을 왼쪽 자식 노드, 오른쪽에 오는 자식을 오른쪽 자식 노드라고 부른다.
다음은 전형적인 이진 트리를 나타내는 그림이다.
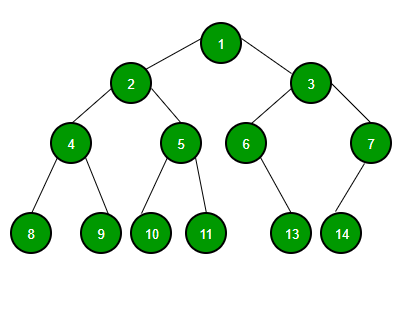
이진 트리의 종류
이진 트리를 구성하는 노드의 형태에 따라 다음과 같이 분류된다.
Full Binary Tree
모든 노드가 자식을 0개 혹은 2개 가진 트리를 일컽는다.
다음은 전부 Full Binary Tree이다.
18
/ \
15 30
/ \ / \
40 50 100 40
18
/ \
15 20
/ \
40 50
/ \
30 50
18
/ \
40 30
/ \
100 40
Full Binary Tree에서 리프노드의 수는 내부노드의 수 + 1 이다.
Complete Binary Tree
트리의 마지막 레벨을 제외한 모든 레벨에서 노드가 자식을 두개 가지고 있고, 마지막 레벨에서는 왼쪽 부터 자식이 빠짐없이 차 있는 트리를 일컽는다.
다음은 전부 Complete Binary Tree 이다.
18
/ \
15 30
/ \ / \
40 50 100 40
18
/ \
15 30
/ \ / \
40 50 100 40
/ \ /
8 7 9
Binary Heap은 Complete Binary 트리이다.
Perfect Binary Tree
리프노드를 제외한 모든 내부노드가 자식 노드를 2개 가지고, 모든 리프노드가 동일 레벨 선상에 있는 트리를 일컽는다.
다음은 전부 Perfect Binary Tree 이다.
18
/ \ --- 높이 h: 3
15 30
/ \ / \
40 50 100 40
18
/ \ -- 높이 h: 2
15 30
Perfect Binary Tree의 높이가 h일 때 $2^h-1$개의 노드를 가진다.
(높이 h: 루트로부터 리프노드 까지의 경로에 있는 노드의 수)
Degenerate (or pathological) tree
트리의 내부노드가 오직 하나의 자식만을 갖는 트리를 일컽는다.
다음은 Degenerate tree 이다.
10
/
20
\
30
\
40
연결 리스트와 성능면에서 동일하다.
이진 트리 표현
이진 트리를 어떻게 표현하고 구현할 수 있을지 알아본다.
이진 트리 클래스는 최상위 노드를 가리키는 root 레퍼런스를 갖고 있다.
class BinaryTree
{
// Root of Binary Tree
Node root;
// Constructors
BinaryTree(int key)
{
root = new Node(key);
}
BinaryTree()
{
root = null;
}
}
또한 이진 트리 클래스는 각 노드를 표현할 노드 클래스를 가지고 있다.
class Node
{
int key;
Node left, right;
public Node(int item)
{
key = item;
left = right = null;
}
}
노드는 다음과 같은 부분으로 구성된다.
- Data - 데이터를 저장하는 필드
- 왼쪽 자식에 대한 레퍼런스
- 오른쪽 자식에 대한 레퍼런스
트리 예제 코드
위의 표현들을 이용하여 트리를 만들어보고 이해해보자.
먼저 전체 코드이다.
/* Class containing left and right child of current
node and key value*/
// A Java program to introduce Binary Tree
class BinaryTree
{
// Root of Binary Tree
Node root;
// Constructors
BinaryTree(int key)
{
root = new Node(key);
}
BinaryTree()
{
root = null;
}
static class Node
{
int key;
Node left, right;
public Node(int item)
{
key = item;
left = right = null;
}
}
public static void main(String[] args)
{
BinaryTree tree = new BinaryTree();
/*create root*/
tree.root = new Node(1);
tree.root.left = new Node(2);
tree.root.right = new Node(3);
tree.root.left.left = new Node(4);
}
}
BinaryTree tree = new BinaryTree();
이진 트리를 생성하는 구문이다.
아직은 아무런 노드가 없으므로 root 레퍼런스는 null이다.
tree.root = new Node(1);
노드를 할당하여 1을 넣고, 트리의 root 레퍼런스가 할당된 노드를 가리키게 한다.
그림으로 표현하면 다음처럼 도식화 된다.
1
/ \
null null
1번 노드는 루트가 되었다.
1번 노드의 왼쪽, 오른쪽 자식노드는 없으므로 left, right 레퍼런스는 null이다.
그 다음을 보자.
tree.root.left = new Node(2);
tree.root.right = new Node(3);
노드를 할당하여 2를 넣고, 트리의 root 왼쪽 자식 레퍼런스가 할당된 노드를 가리키게 한다. 노드를 할당하여 3을 넣고, 트리의 root 오른쪽 자식 레퍼런스가 할당된 노드를 가리키게 한다. 2, 3번 노드는 아직 자식들이 없으므로 left, right 레퍼런스는 null이다.
그림으로 표현하면 다음과 같다.
1
/ \
2 3
/ \ / \
null null null null
계속해서 그 다음을 보자.
tree.root.left.left = new Node(4);
노드를 할당하여 4를 넣고, root의 왼쪽 노드의 왼쪽 자식 레퍼런스가 할당된 노드를 가리키게 한다.
그림으로 표현하면 다음과 같다.
1
/ \
2 3
/ \ / \
4 null null null
/ \
null null
4번 노드는 2번 노드의 자식이 되었다.

Leave a comment