삽입 정렬(Insertion sort)
삽입 정렬은 안정 정렬이자 제자리 정렬 알고리즘이다.
비교적 심플한 정렬 알고리즘으로서 일상 생활에서도 번호에 따라 카드를 정렬할 때 대부분 이 방법을 사용하곤 한다. 이 알고리즘에서는 각 원소를 정렬된 부분 배열(Sorted partial array)의 적절한 위치에 삽입한다.
삽입 정렬의 시간복잡도는 최악 기준 $O(n^2)$이므로 큰 리스트에는 비효율적이며, 유사한 시간복잡도를 갖는 선택 정렬이나 버블소트 보다는 성능이 좋지만, $O(nlogn)$의 시간복잡도를 같는 퀵 소트나 머지소트 같은 소팅 알고리즘 보다는 덜 효율적이다.
그러나, 삽입 정렬은 원소의 숫자가 적은 배열이나 리스트(원소의 개수가 10-20개 이하)에서는 일반적으로 퀵 소트나 머지소트 보다 효율적이여서, 실무에서는 다른 $O(nlongn)$의 시간복잡도를 갖는 소팅 알고리즘과 함께 정렬에 사용되어지고 있다. (ex. Tim sort)
안정 정렬과 제자리 정렬 이란?
안정 정렬: 정렬이 끝나면 같은 키값을 가진 원소들의 상대적인 순서가 변하지 않는 것을 의미.
안정 정렬 알고리즘으로는 삽입 정렬, 머지소트, 카운팅 소트 등이 있다.
제자리 정렬: 원소들의 개수에 비해서 충분히 무시할 만한 저장 공간만을 더 사용하는 정렬 알고리즘들을 의미.
예를 들어 삽입 정렬은 이미 주어진 원소들을 옮긴 뒤 적절한 위치에 원소를 삽입하는 연산을 반복하는데, 이 과정에서 원소들을 담는 공간 외에 추가로 사용될 수 있는 공간은 옮겨지는 원소가 저장되는 공간과 루프 변수 정도에 불과하다.
다음은 삽입 정렬의 몇 가지 장점이다.
- 다른 정렬 알고리즘에 비해 코드가 간단하고 구현이 쉽다. - Simple to implement
- 최악 기준 $O(n^2)$의 시간복잡도를 가지는 소팅 알고리즘(선택 정렬, 버블 소트)에 비해 비교적 효율적이다.
- 작은 데이터 셋에서 매우 효율적이다. - Efficient in small data set
- 적응적이다. 대체로 이미 정렬이 되어있는 데이터 셋에서 효율적이다. - Adaptive
- 같은 키값을 가진 원소들의 상대적인 순서를 바꾸지 않는다. - Stable
- O(1)의 상수적인 추가 메모리 공간만이 필요하다. - In-place
- 실시간으로 원소를 하나씩 입력받으면서 정렬할 수 있다. - Online
알고리즘
다음은 삽입 정렬의 알고리즘이다. (오름차순, 원소 개수 2개 이상 기준)
- 먼저, 정렬될 리스트에서 두번째 원소를 선택한다.
- 1.번에서 선택한 원소를 기준으로 리스트의 앞의 원소들과 비교하여 기준에 따라 자기 자리를 찾아간다. - 1 pass
- 이를 매번 3…n-1번째 원소까지 선택하여 2.번을 반복한다.
이처럼, n개의 원소를 가진 리스트는 삽입 정렬로 n-1번의 패스를 거쳐 정렬이 된다.
삽입 정렬에서는 매 반복(1 pass or each repetition)마다 하나의 원소를 취해 부분 정렬된 정렬된 리스트에 그 원소가 속할 위치를 찾고 그 위치에 삽입을 한다. 이것을 n번째 원소까지 반복한다.
다음 그림은 매번의 반복마다 원소 $x$가 자리를 찾아 삽입되는 것을 보여준다.
아래 그림은 원소 $x$가 정렬이 수행되기 전이다.
원소 $x$는 아직 정렬되지 않은 데이터 셋에 있다.

정렬이 수행되고 나서는 아래 그림처럼 된다.
원소 $x$는 $<=x$ 보다는 오른쪽 $>x$ 보다는 왼쪽에 있어, 부분 정렬 결과에 속하게 된다.
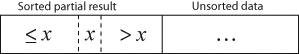
다음은 삽입 정렬의 애니메이션이다.
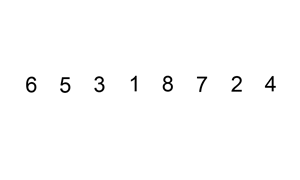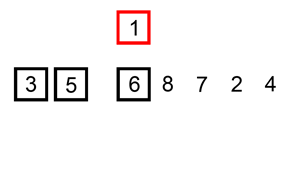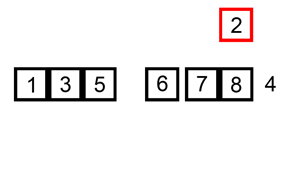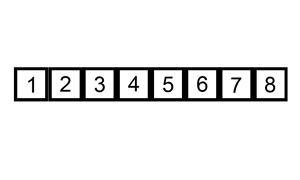
예제
다음 예제를 보고 알고리즘을 이해해 보자.
다음과 같은 리스트가 있다고 하자.
List = [64 25 12 22 11] - index: 0...4
List = [정렬 완료 | 미정렬]
1 pass: 1번 인덱스 위치의 원소를 선택하여
앞의 원소들과 비교하여 적절한 위치에 삽입한다.
List = [25 64 | 12 22 11]
2 pass: 2번 인덱스 위치의 원소를 선택하여
앞의 원소들과 비교하여 적절한 위치에 삽입한다.
List = [12 25 64 | 22 11]
3 pass: 3번 인덱스 위치의 원소를 선택하여
앞의 원소들과 비교하여 적절한 위치에 삽입한다.
List = [12 22 25 64 | 11]
4 pass: 4번 인덱스 위치의 원소를 선택하여
앞의 원소들과 비교하여 적절한 위치에 삽입한다.
List = [11 12 22 25 64 | ]
n-1번의 pass로 리스트의 정렬이 완료되었다.
List = [11 12 22 25 64]
구현
다음은 삽입 정렬의 의사 코드이다.
i ← 1
while i < length(A)
j ← i
while j > 0 and A[j-1] > A[j]
swap A[j] and A[j-1]
j ← j - 1
end while
i ← i + 1
end while
다음은 선택 정렬을 C++로 구현한 코드이다.
#include<iostream>
using namespace std;
int main ()
{
int i,j, k,temp;
int a[10] = { 10, 9, 7, 101, 23, 44, 12, 78, 34, 23};
cout<<"\nprinting sorted elements...\n";
for(k=1; k<10; k++)
{
temp = a[k];
j= k-1;
while(j>=0 && temp <= a[j])
{
a[j+1] = a[j];
j = j-1;
}
a[j+1] = temp;
}
for(i=0;i<10;i++)
{
cout <<a[i]<<"\n";
}
}
/*
Output:
Printing sorted elements . . .
7
9
10
12
23
23
34
44
78
101
*/
다음은 선택 정렬을 java로 구현한 코드이다.
public class InsertionSort {
public static void main(String[] args) {
int[] a = {10, 9, 7, 101, 23, 44, 12, 78, 34, 23};
for(int k=1; k<10; k++)
{
int temp = a[k];
int j= k-1;
while(j>=0 && temp <= a[j])
{
a[j+1] = a[j];
j = j-1;
}
a[j+1] = temp;
}
System.out.println("printing sorted elements ...");
for(int i=0;i<10;i++)
{
System.out.println(a[i]);
}
}
}
/*
Output:
Printing sorted elements . . .
7
9
10
12
23
23
34
44
78
101
*/
시간복잡도 & 공간복잡도
시간복잡도 분석
최악 기준 $1$…$n-1$개의 원소를 매 패스마다 비교한다. n개의 원소가 있다면 $n-1$의 패스를 가진다.
\[1 + 2 +...+ (n-1) = {\frac {1}{2}}n(n-1)={\frac {1}{2}}(n^{2}-n)\]비교의 측면에서 볼 때, 복잡도는 $O(n^2)$이다.
교환(Swap)도 위와 동일하다.
**Insertion sort**
Class 정렬 알고리즘
Data structure 배열
Worst-case О(n^2) 비교
performance О(n^2) 교환
Best-case О(n^2) 비교
performance О(n^2) 교환
Average О(n^2) 비교
performance О(n^2) 교환
Worst-case O(n) 총 공간
space complexity O(1) 추가 공간

Leave a comment