Bubble(버블 정렬)
비교 기반 정렬 알고리즘이다.
정렬이 실행되면서 마치 형태가 거품이 수면위로 떠오르는 것 같은 모양을 한다고 하여 붙여진 이름이다.
인접한 두 원소를 비교하여 기준에 따라 스왑하고, 한 칸씩 옆으로 가면서 이를 n번째 원소까지 반복한다.
이를 모든 원소에 대해 n번 반복한다.
(최적화를 하면 배열의 원소 위치상태에 따라 횟수가 n번 보다 낮아질 수 있다.)
다른 O(nlongn)의 성능을 내는 정렬 알고리즘에 비해 성능이 좋지 않으므로 실무에서는 사용되지 않고 교육용 목적으로 사용 되어진다.
더 효율적인 정렬 알고리즘인 팀소트(Timsort)나 머지소트(Merge sort)가 인기있는 프로그래밍 언어(java, python)의 내장 정렬 라이브러리로 사용되고 있다.
Algorithm
밑의 애니메이션을 먼저 보고 알고리즘을 읽으면 이해가 빠를 수 있다.
- 처음 원소를 시작으로 n번째 원소까지 차례대로 인접한 원소와 오른쪽으로 비교하며 스왑을 진행한다.
- n번째 원소와 비교가 끝이나면 n번째 원소는 정렬이 완료된 것이다.
- 다시 처음 원소부터 n-1번째 원소까지 인접한 원소와 비교하며 필요하면 스왑을 한다.
- n-1번째 원소와 비교가 끝이나면 n-1번째 원소는 정렬이 완료된 것이다.
- 이를 반복하여, n-2..n-3..2번째 원소까지 정렬이 완료되면 알고리즘은 끝이난다.
Animation - Bubble sort
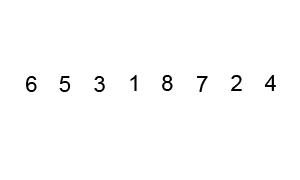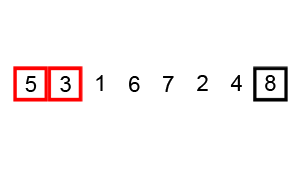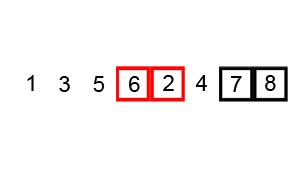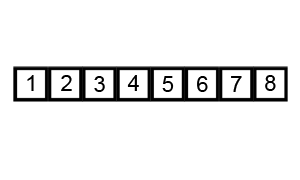
Analysis
버블소트는 최악과 평균 시간복잡도가 $O(n^2)$인 (2중 루프로 인해) 정렬 알고리즘이다.
최악과 평균 시간복잡도가 $O(nlog_{2}n)$인 실용적인 정렬 알고리즘 보다 성능이 좋지않고
시간복잡도가 $O(n^2)$인 삽입정렬도 버블소트보다는 빠르게 동작하기 때문에 버블소트는 다소 실용적인 정렬 알고리즘이 아니다.
다른 정렬들과 비교해(삽입정렬을 제외한) 버블소트의 최대 장점은 배열이 정렬되어 있는 것을 탐지해낼 수 있는 능력이다.
리스트가 정렬이 완료되어 있을 때의 버블정렬은 O(n)이다.
Step-by-step example
배열 [5 1 4 2 8]이 있다고 하자.
처음 원소부터 끝 원소까지 오름차순으로 버블소트를 이용하여 정렬하려고 한다.
첫번째 패스
( 5 1 4 2 8 ) → ( 1 5 4 2 8 )
첫번째 원소와 두번째 원소를 비교한다, 5 > 1 이므로 스왑한다.
( 1 5 4 2 8 ) → ( 1 4 5 2 8 )
두번째 원소와 세번째 원소를 비교한다, 5 > 4 이므로 스왑한다.
( 1 4 5 2 8 ) → ( 1 4 2 5 8 )
세번째 원소와 네번째 원소를 비교한다, 5 > 2 이므로 스왑한다.
( 1 4 2 5 8 ) → ( 1 4 2 5 8 )
네번째 원소와 다섯번째 원소를 비교한다, 5 < 8 이므로 그대로 둔다.
첫번째 패스가 끝났다.
두번째 패스
( 1 4 2 5 8 ) → ( 1 4 2 5 8 )
첫번째 원소와 두번째 원소를 비교한다, 1 < 4 이므로 그대로 둔다.
( 1 4 2 5 8 ) → ( 1 2 4 5 8 )
두번째 원소와 세번째 원소를 비교한다, 4 > 2 이므로 스왑한다.
( 1 2 4 5 8 ) → ( 1 2 4 5 8 )
세번째 원소와 네번째 원소를 비교한다, 4 < 5 이므로 그대로 둔다.
( 1 2 4 5 8 ) → ( 1 2 4 5 8 )
첫번째 원소와 두번째 원소를 비교한다, 5 < 8 이므로 그대로 둔다.
두번째 패스가 끝났다.
이제, 배열은 이미 오름차순으로 정렬이 완료되었다.
그러나, 알고리즘은 정렬이 완료되었는지 아직 모른다.
정렬이 완료되었는지 알기 위해선 하나의 패스를 더 거쳐야 한다.
(불리언 변수 하나를 두어 이를 알 수 있는데, 밑의 구현에서 알아본다.)
세번째 패스
( 1 2 4 5 8 ) → ( 1 2 4 5 8 )
( 1 2 4 5 8 ) → ( 1 2 4 5 8 )
( 1 2 4 5 8 ) → ( 1 2 4 5 8 )
( 1 2 4 5 8 ) → ( 1 2 4 5 8 )
세번째 패스가 끝났다.
스왑된 원소가 없으므로 알고리즘은 더 이상 패스를 수행하지 않는다.
알고리즘을 종료한다.
Implementation
다음은 버블소트를 의사코드로 구현한 것이다.
버블소트 의사코드 구현 (index is 0 base)
procedure bubbleSort(A : list of sortable items)
n := length(A) // 배열 길이, 원소 개수
repeat // 반복한다.
swapped = false // 스왑이 되었는지 여부
for i := 1 to n - 1 inclusive do // [1 ~ n-1]까지
/* 만약 두 원소가 순서에 어긋나면 */
if A[i - 1] > A[i] then
/* 스왑하고, 스왑되었다는 것을 체크한다. */
swap(A[i - 1], A[i])
swapped := true
end if
end for
// 스왑이 안되었을때 까지, 즉, swapped가 true면 repeat로 간다.
until not swapped
end procedure
버블소트 최적화
n번째 패스가 끝이나면 n번째로 큰 원소는 이미 정렬이 완료되어 그자리에 위치가 변하지 않기에, 내부 루프는 매 패스마다, 0번째 부터 n번째 까지 원소를 비교할 필요가 없다.
한번의 패스가 끝이나면 n을 n-1로, 즉 1씩 줄여 쓸때없는 연산을 피할 수 있다.
procedure bubbleSort(A : list of sortable items)
n := length(A)
repeat
swapped := false
for i := 1 to n - 1 inclusive do
if A[i - 1] > A[i] then
swap(A[i - 1], A[i])
swapped = true
end if
end for
// n을 1 감소시켜 다음번 패스 때 불필요한 연산을 하지 않는다.
n := n - 1
until not swapped
end procedure
한가지 더 최적화를 해보자.
한 번의 패스로 하나 이상의 원소가 최종 정렬된 자리에 올 수 있다.
그렇다면 우리는 최종 정렬된 원소를 굳이 비교하지 않고 스킵할 수 있다.
다음은 이를 구현한 슈도 코드이다.
새로운 변수 newn을 주목하라.
procedure bubbleSort(A : list of sortable items)
n := length(A)
repeat
// newn: 몇 번째 원소까지 비교가 완료 되었는지
newn := 0
for i := 1 to n - 1 inclusive do
if A[i - 1] > A[i] then
swap(A[i - 1], A[i])
newn := i
end if
end for
n := newn
// n이 1보다 작거나 같으면 반복문을 빠져 나온다.
until n ≤ 1
end procedure
[3 2 1 4 5]인 배열이 있다고 해보자.
첫번째 패스를 거치면
인덱스 0~4번 까지 비교를 하게 된다.
[2 1 3 4 5]가 된다.
이 때, newn은 2가 된다.
이는 2번 인덱스에서 마지막으로 스왑이 되었고, 그 이후로는 스왑이되지 않았다.
즉, 그 이후로는 정렬이 완료되었으니 정렬이 불필요하다는 것을 의미한다.
두번때 패스에서는
원래 대로라면 인덱스 0~3번 까지 비교를 하게 되겠지만
최적화를 거치면 첫번째 패스에서 newn은 2인 것을 아니까
인덱스 0~3, 0~2를 스킵하고, 0~1번 까지만 비교가 진행되게 된다.
이로서 불필요한 패스를 줄임으로서 최악 기준 약 50%의 성능 향상을 기대할 수 있다.
시간복잡도
최악 시간복잡도 $O(n^2)$
최선 시간복잡도 $O(n)$ - 배열이 이미 정렬 완료되었을 때
평균 시간복잡도 $O(n^2)$

Leave a comment