CNN(Convolutional Neural Network)
CNN(Convolutional Neural Network)에서 가장 중요한 연산은 Convolution 입니다.
Convolution의 정의, convolution 연산 방법과 기능에 대해 배웁니다.
그리고 Convolution, 입력을 축소하는 Pooling layer, 모든 노드를 연결하여 최종적인 결과를 만드는 Fully connected layer로 구성되는 기본적인 CNN(Convolutional Neural Network) 구조에 대해 배웁니다.
CNN consists of convolution layer, pooling layer, and fully connected layer.
가장 기본적이고 고전적인 CNN은 feature 값을 얻어내기 위해 합성곱 연산을 하는 convolution layer, Convolution을 거쳐서 나온 activation maps이 있을 때, 이를 이루는 convolution layer을 resizing하여 새로운 layer를 얻는 pooling layer 그리고 우리가 최종적으로 얻고자 하는 값들을 만들어주는 fully connected layer로 구성됩니다.
이미지를 예로 들면, Convolution and pooling layer는 이미지에서 어떤 유용한 정보를 뽑아내는 feature extraction을 담당하고 fully connected layer는 decision making; 예를 들어 분류를 하거나 회귀를 해서 우리가 원하는 출력 값을 얻도록 하게 합니다.
최근 들어서는 뒷단에 있는 fully connected layer가 최소화 되고, 점점 없어지는 추세라고 합니다.
이것은 패러매터의 수와 연관이 있는데요, 패러미터의 수가 늘어 나면 늘어날 수록 학습이 어렵고, Generalization performance가 떨어진다고 알려져 있습니다.
그래서 CNN의 응용 모델에서는 이런 패러매터의 수를 줄이면서 굉장히 Deep한 모델을 만들기 위해 여러 기법이 동원되고 적용되고 있습니다.
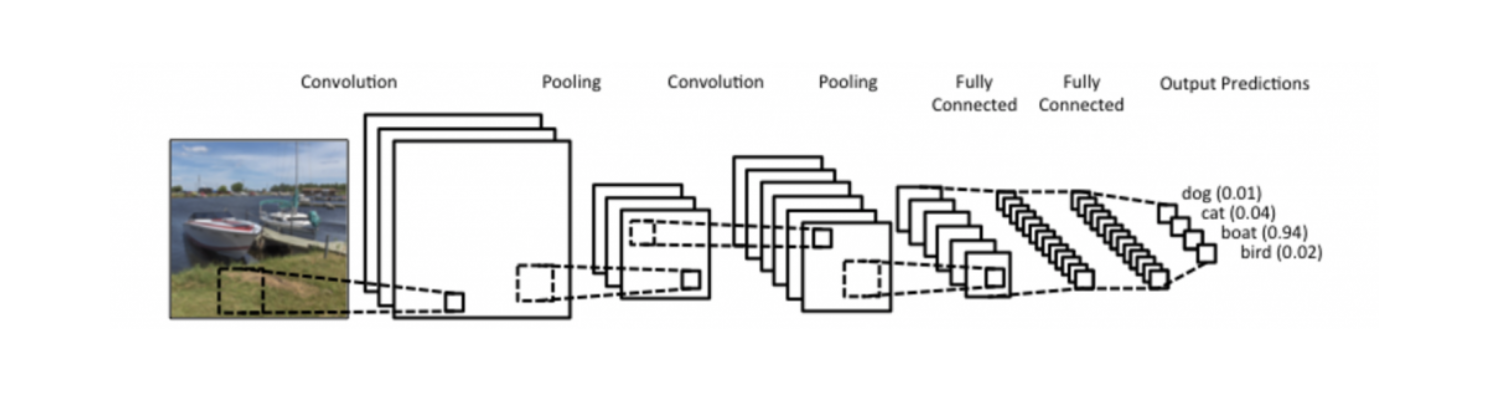
Convolution
Convolution 연산을 밑의 그림을 통해 봐보겠습니다.
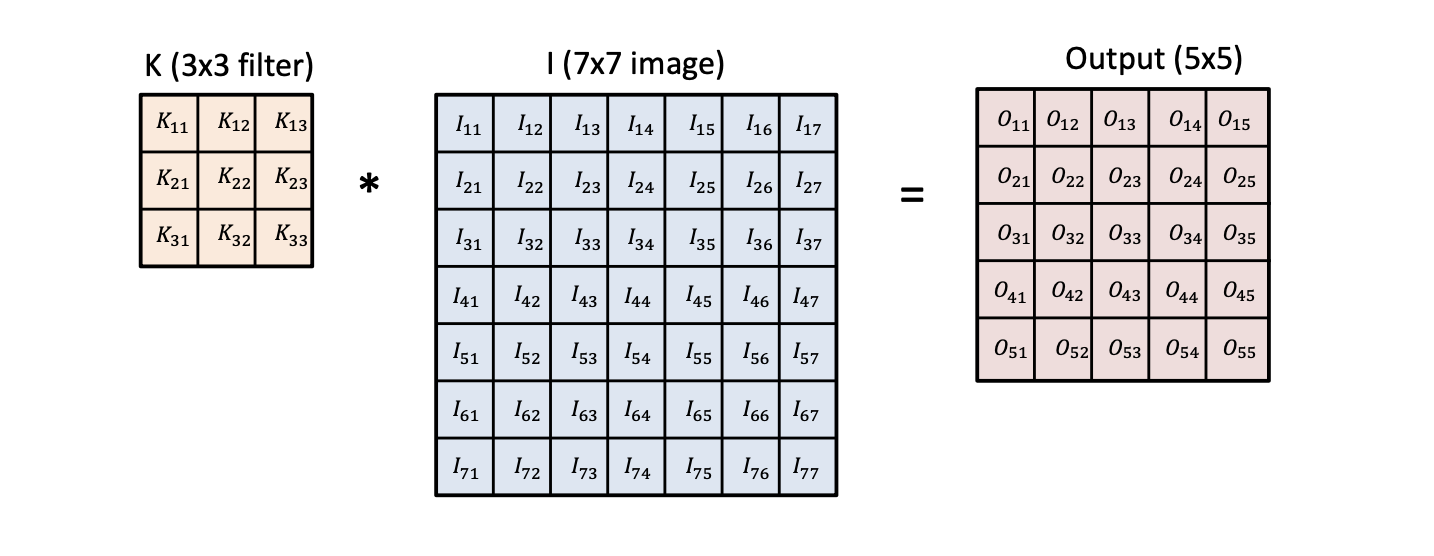
밑에서 알아보게 될 stride와 padding는 고려하지 않고 가장 기본적인 Convolution 연산을 해보면 오른쪽의 Output 필터가 도출되게 됩니다.
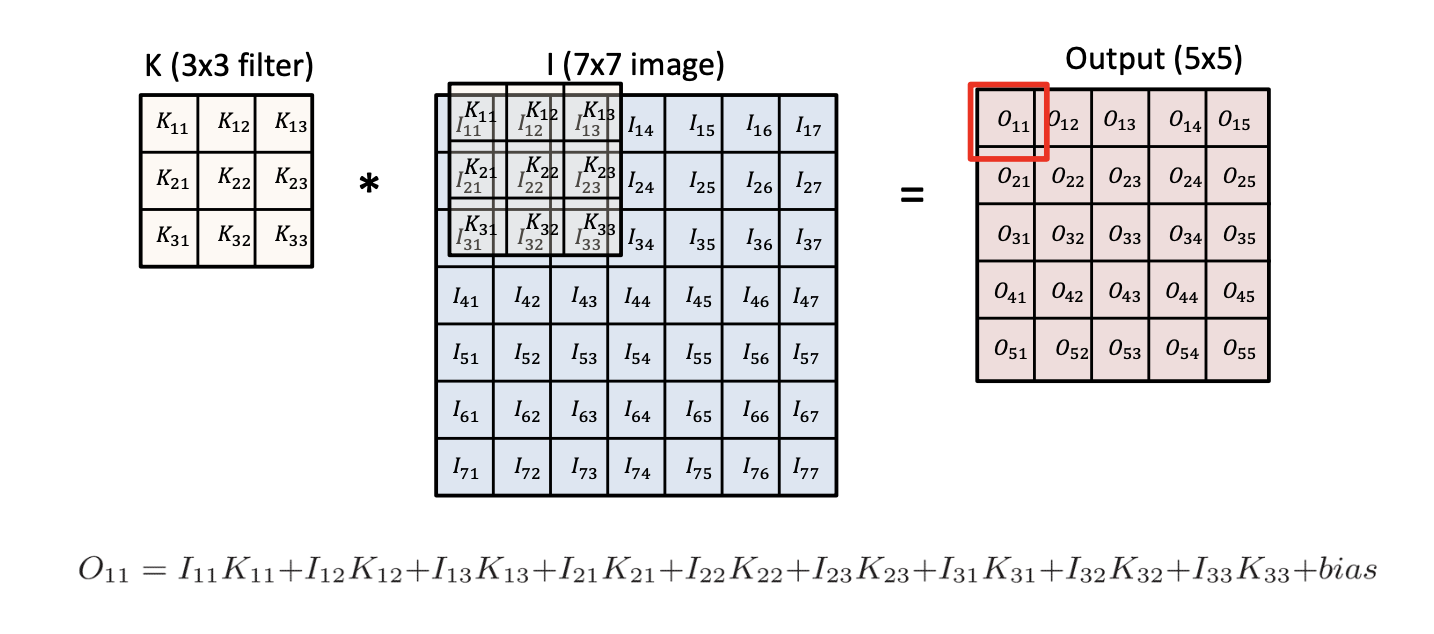
오른쪽에서 빨간 네모인 값, 즉 하나의 Output 값은 Convolution 필터를 적용하고자 하는 이미지에 찍어 도출한다고 생각할 수 있습니다.
위의 그림에서 보는 것 처럼, 필터를 좌측 상단 이미지 상에 위치시키고, 각 그리드 위치에 맞는 값들 끼리 서로 곱셈을 한 후 전부 더하면 O_11의 output 값이 됩니다.
추가로 마지막에 바이어스 텀을 더해줄 수 있습니다.
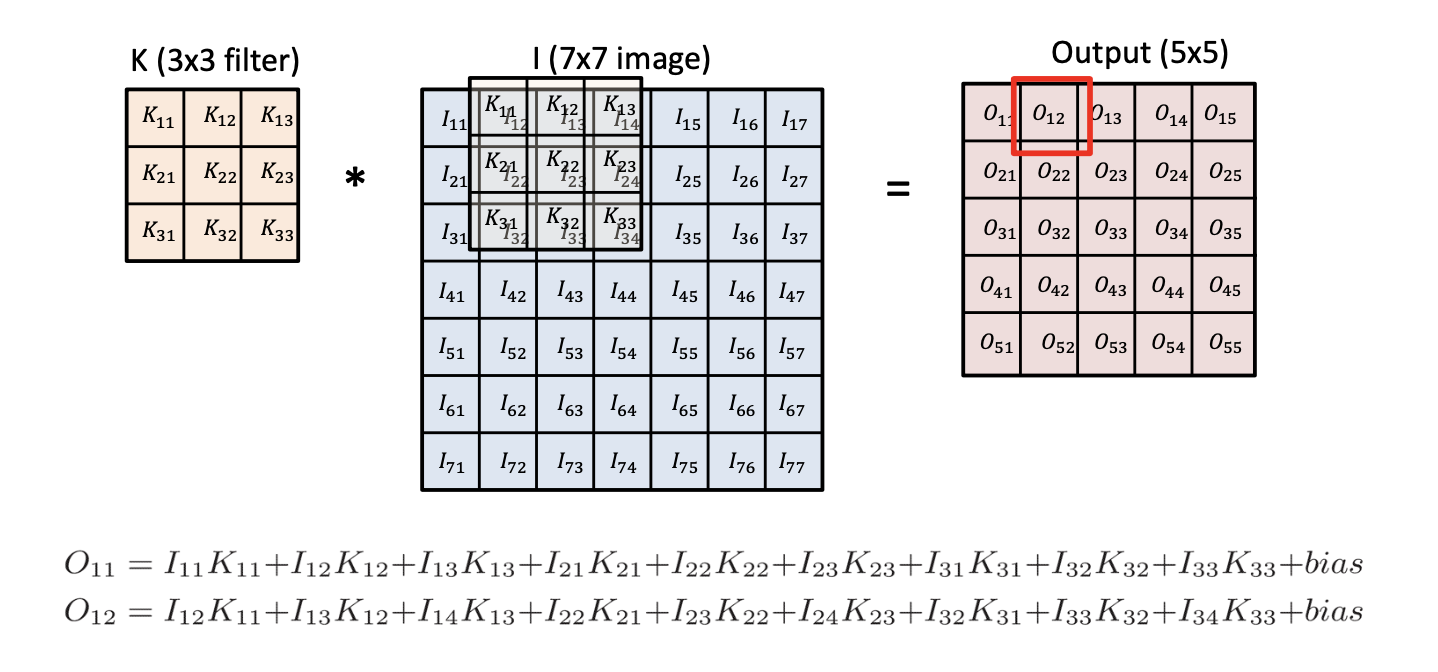
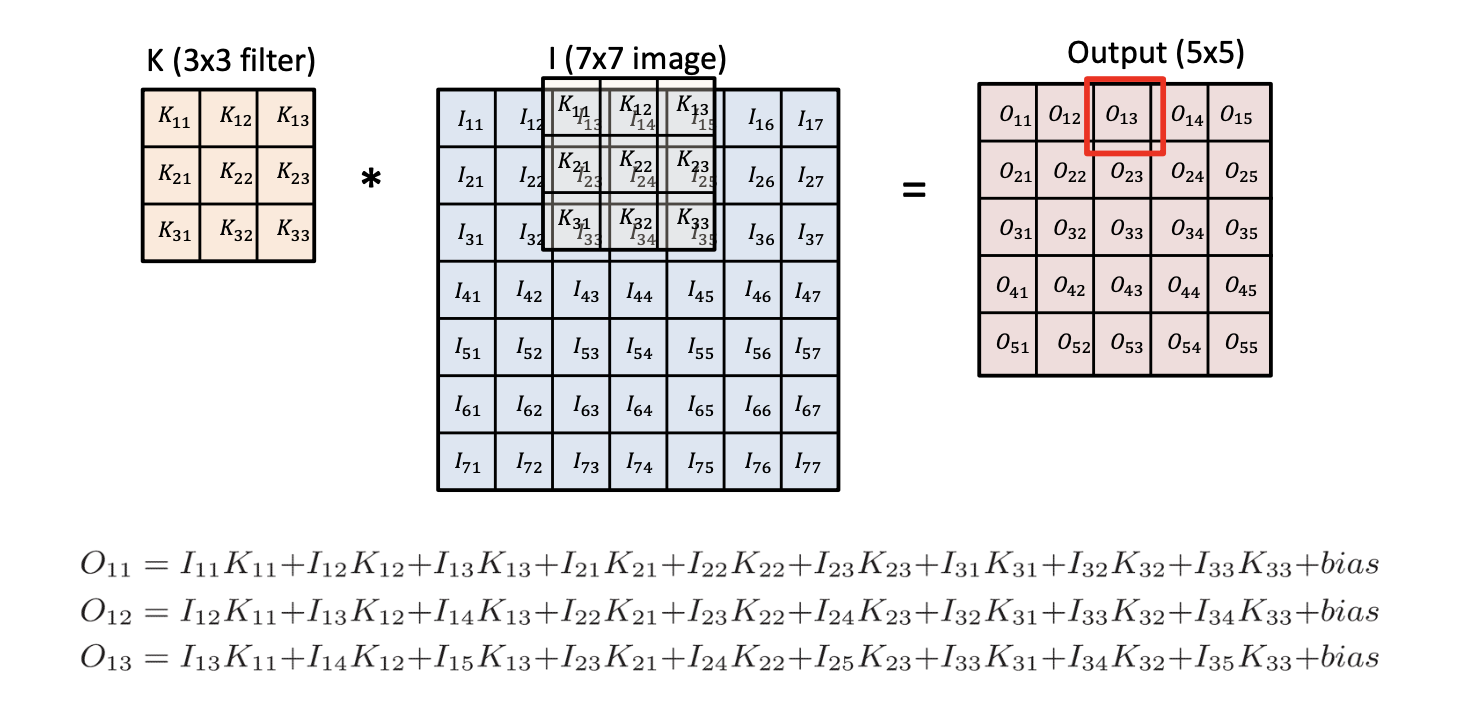
전과 마찬가지로 O_12, O_13 값도 이미지 상에서 필터를 한 칸씩 옆으로 밀어 똑같이 계산하면 도출할 수 있습니다.
2D convolution in action
이미지 상에서 convolution operation을 한다는 것은 어떤 의미가 있을까요?
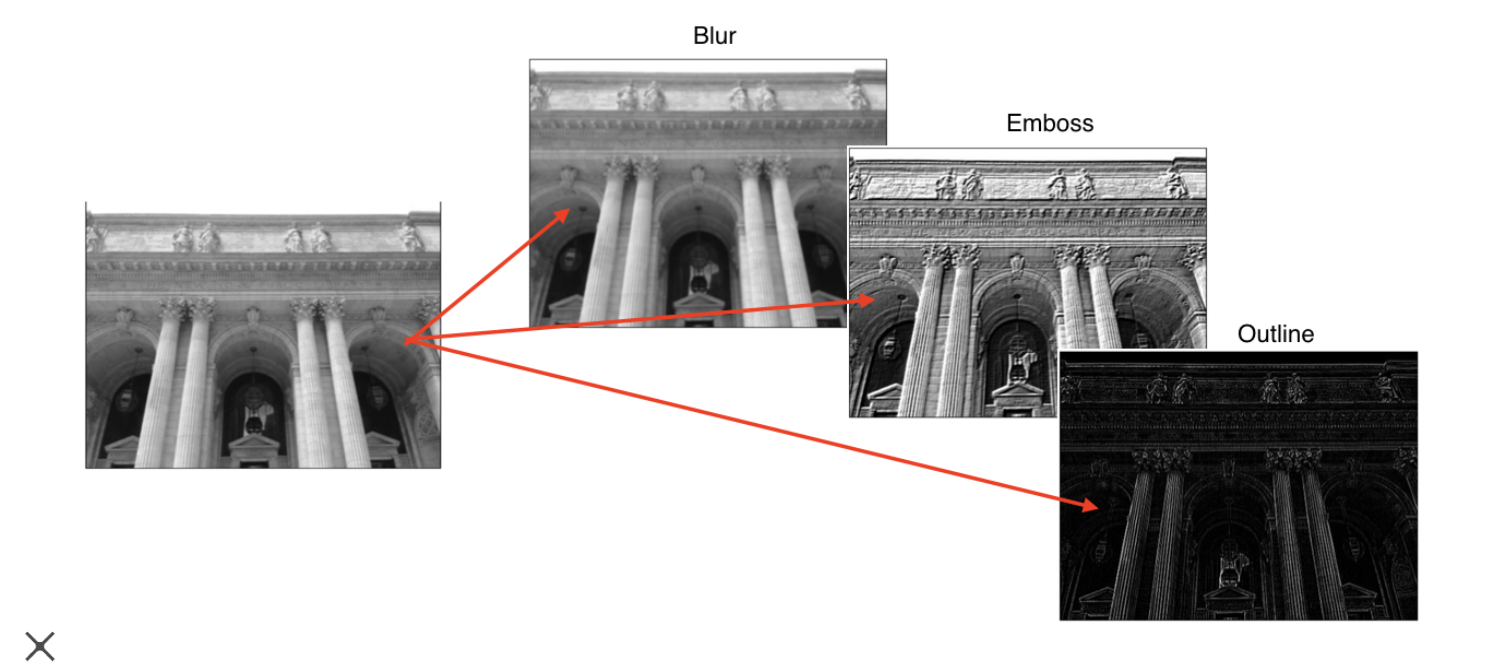
우리가 적용하고자 하는 필터에 따라 같은 이미지에 대해서 convolution output이 밑에서 보이는 것 처럼 여러가지 타입의 이미지로 변환이 되게 됩니다.
예를 들어서, 1/9 값을 가진 3x3 필터를 사용한다면, 이미지 상에서 필터가 적용될 때 3x3 픽셀의 이미지 값의 평균이 계산되고 이는 output 값에서 한 픽셀의 값이 됩니다. 그래서 이미지의 특정 영역에 대해 픽셀 값을 다 합쳐서 평균을 내므로 마치 밑에서 보이는 것 처럼 예를 들면 Blur화 된 이미지가 만들어지게 되는 것입니다.
마찬가지로 다른 타입의 필터를 적용하면 같은 이미지에 대해 강조되거나 외곽이 강조된 이미지를 얻을 수 있을 것입니다.
RGB Image Convolution
일반적으로 CNN에서는 RGB 이미지를 많이 다루게 됩니다.
대체로, 이미지는 가로와 세로 길이 그리고, RGB 값을 의미하는 3개의 채널로 구성이 됩니다.
RGB 이미지에 대해 Convolution을 하게 되면 이미지의 채널과 적용하고자 하는 필터의 채널 수를 맞춰서 계산하게 됩니다.
그래서 Output은 가로와 세로 모두 32-5+1인 크기가 되고 Depth즉 채널의 수는 1이 됩니다.
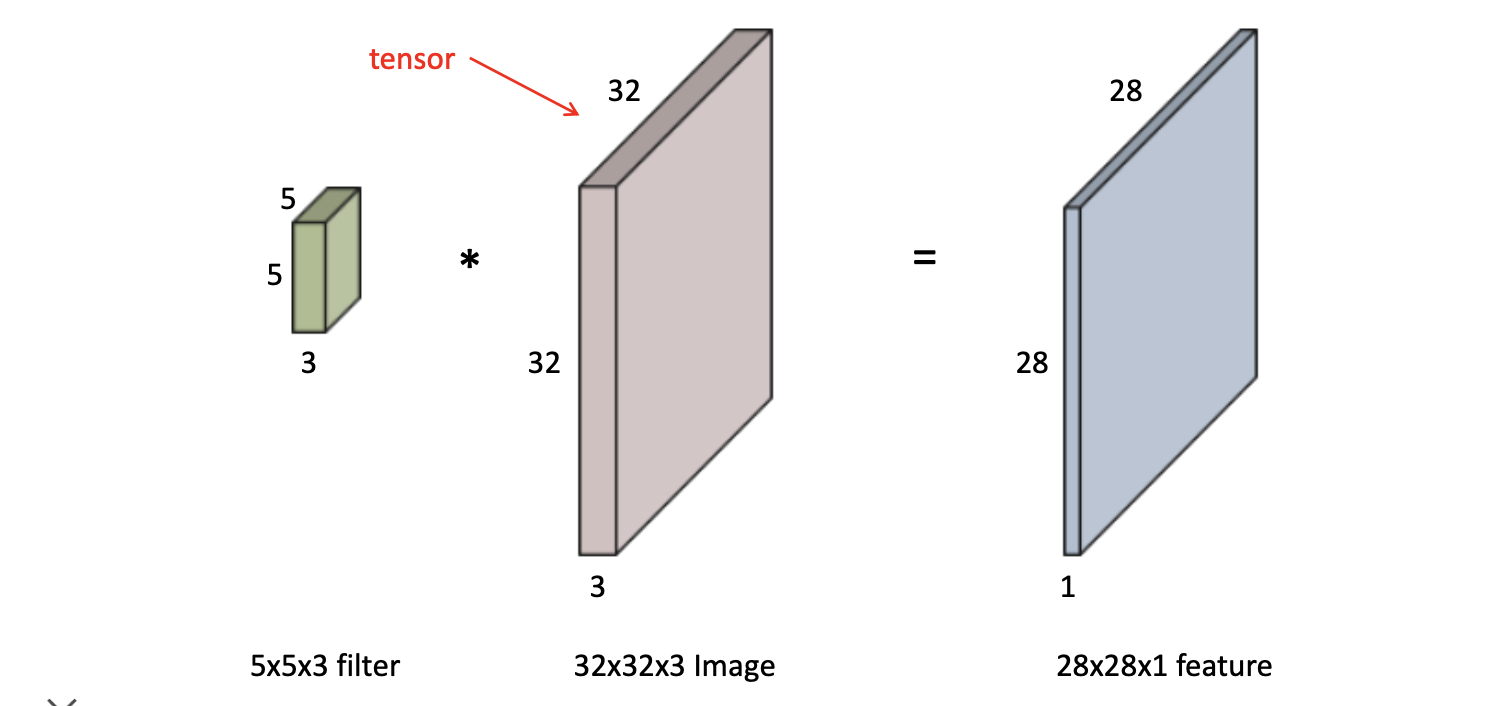
하나의 이미지에 대해 하나의 필터를 적용하게 되면 깊이 즉, 채널이 1인 feature 맵이 나오게 됩니다.
feature맵의 채널 수를 늘리고 싶다면, 하나의 이미지에 대해 여러개의 서로 다른 filter를 사용해서 연산을 하게 되면 feature맵의 채널 수가 filter개수 만큼 늘어나게 됩니다.
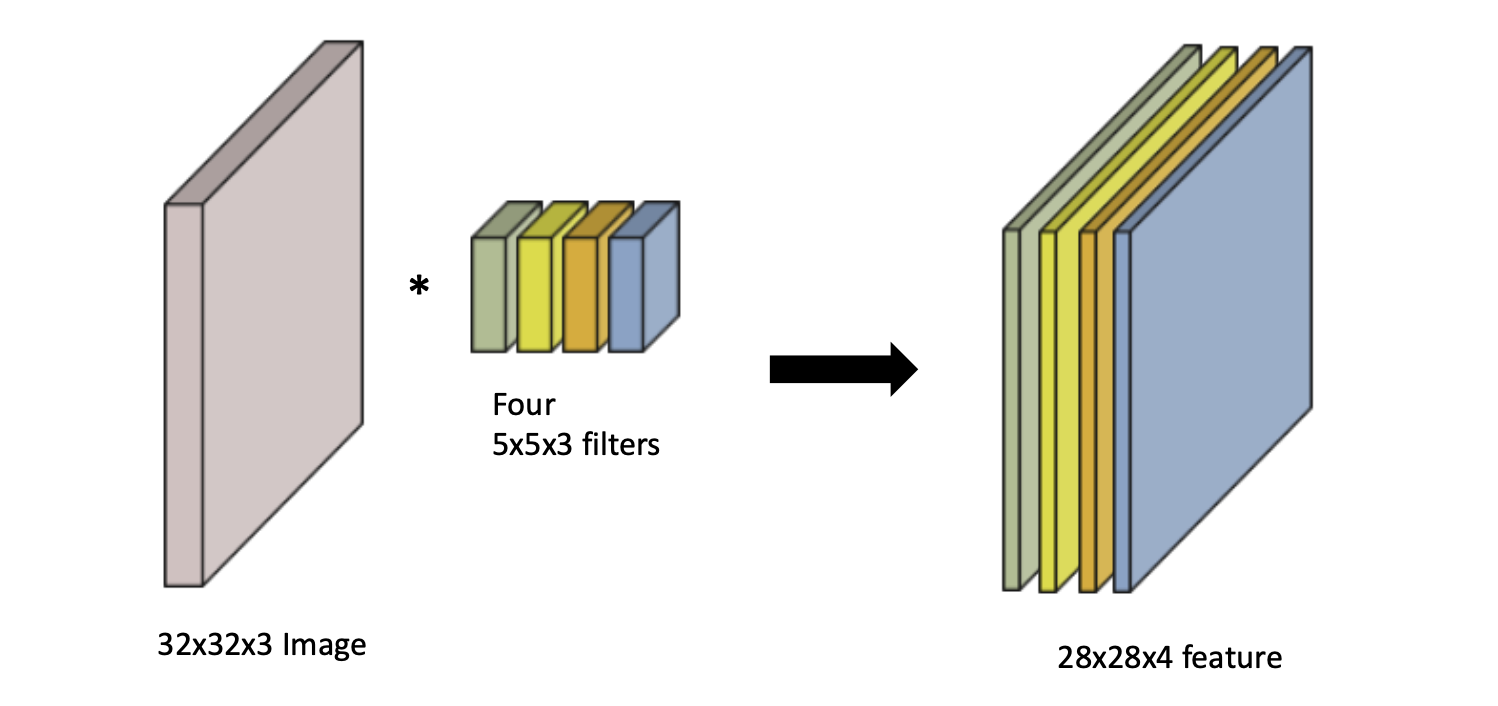
Convolution 연산을 여러 번 하게 되면 아래 그림처럼 도식화 될 수 있습니다.
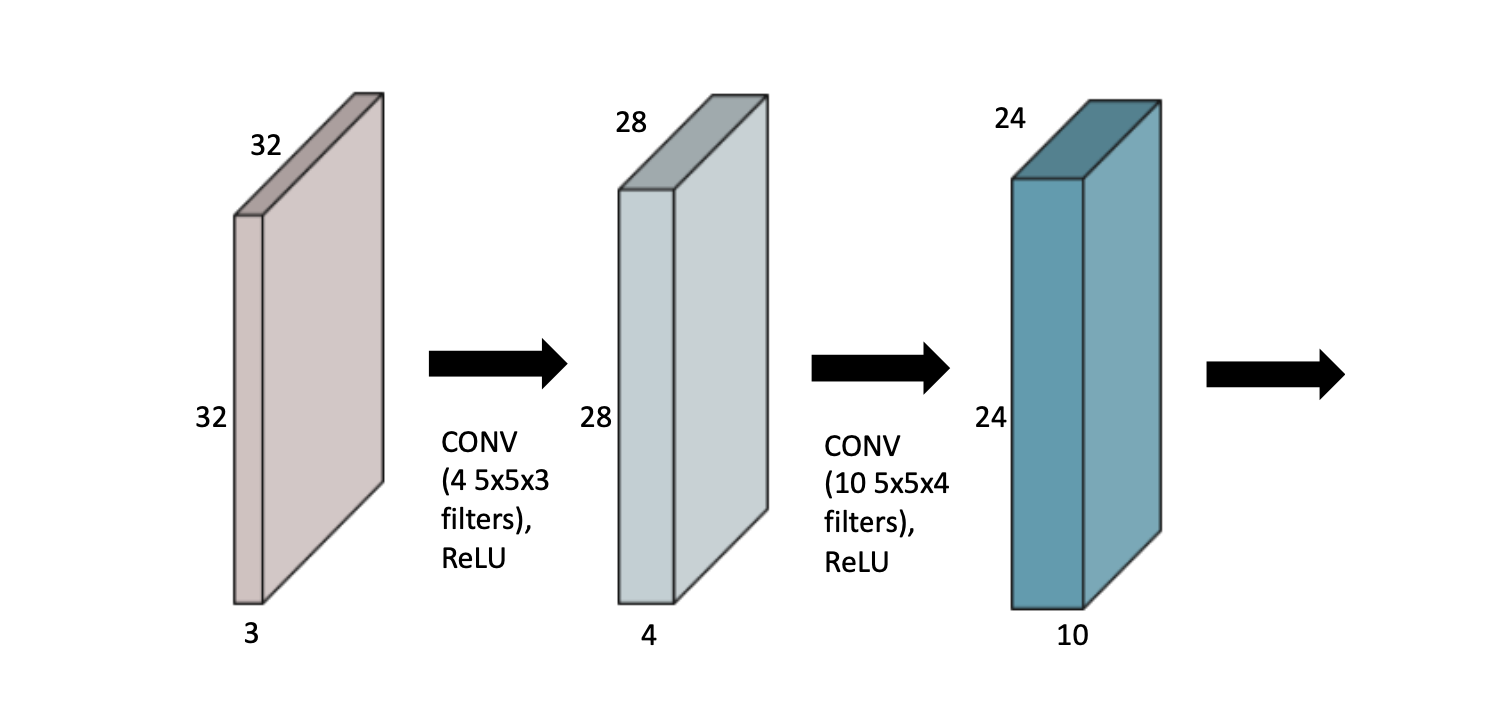
stride는 1, padding은 0으로 고려하고 도식화 된 이미지 입니다.
32x32x3의 이미지에 대해 5x5x3의 필터가 적용되게 되는데, 필터의 개수가 4개 이므로 결과물을 28x28x4가 됩니다. (적용하는 필터의 개수 = 출력의 채널 수) 그리고 한 번 Convolution이 거치게 되면 생성된 feature맵의 각각의 Element들에 대해 Non-linear activation function을 적용하게 됩니다.
ReLU를 적용시키게 되면, 0보다 작은 Element 값들은 0 이되고, 0보다 큰 값들은 그대로 나오게 됩니다.
그리고 다시 이 feature맵에 대해 5x5x4의 필터 10개를 적용하게 되면 그림과 같이 나오게 됩니다.
나중에 보게 되겠지만 이 그림에서 첫번 째 Convolution에서 적용된 패러매터 들의 개수는 5x5x3x4가 됩니다.
4개의 필터가 필요하고, 각 필터의 사이즈는 5x5x3가 되기 때문입니다.
Stride
Stride라는 말은 쉽게 생각해 넓게 걷는다 라는 의미가 됩니다.
Convolution에서 Stride가 1이란 말은 이미지 상에서 매 픽셀마다 필터를 한 번에 한 픽셀 씩 옮겨 적용한다고 생각하면 이해가 쉽습니다.
위에서 보았던 Convolution 연산들은 이미지에 대해 필터가 한 번에 한 칸씩 이동하며 적용이 되었습니다. 그래서 Stride가 1이 됩니다.
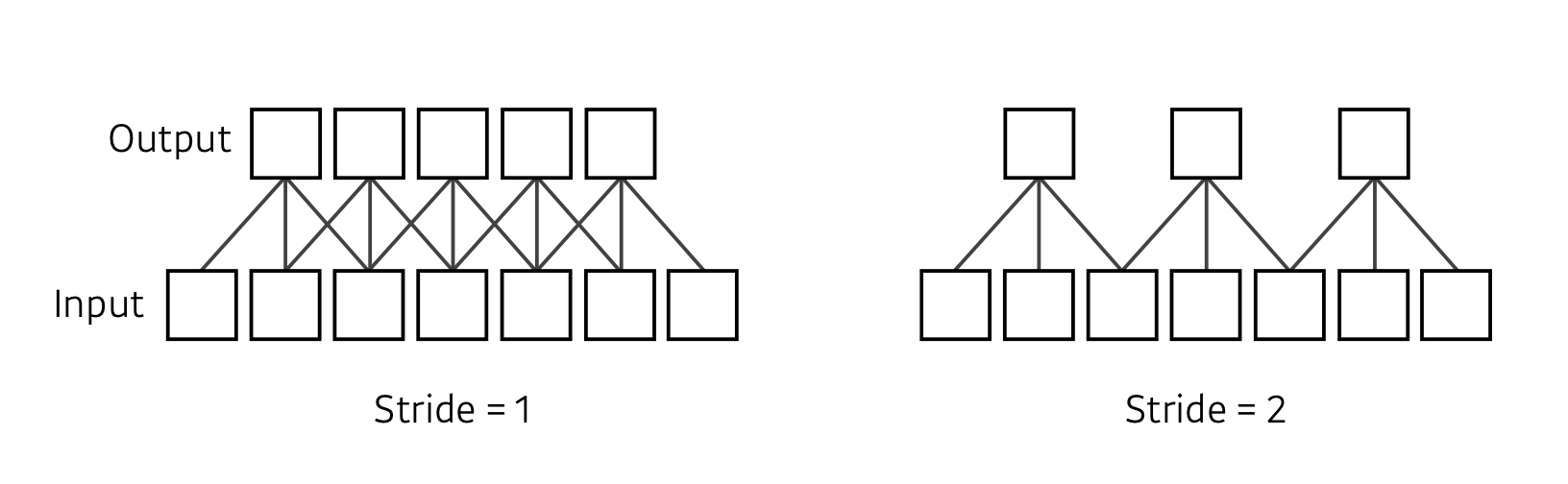
왼쪽 그림에서 Input에 대해 크기가 3인 필터를 적용하고 Stride가 1이라면 Output은 5가 됩니다. 한 번에 한 칸씩 가므로.
Stride가 2인 경우에는 처음에 필터가 적용되고 나서 Stride의 수 만큼 옆으로 필터가 이동하게 됩니다. 따라서 Output은 3개가 나오게 됩니다.
위에서는 1차원을 예로 들었지만 2차원이 되면, Stride도 (1, 1), (2, 3) 이렇게 표현 될 수 있습니다.
Padding
위에서 보았듯이 이미지에 대해 필터를 3x3을 적용하고 나온 출력은 원래 이미지의 크기와 같지 않고 축소 되었습니다. 왜냐하면 boundary 정보가 버려지기 때문입니다. 필터가 이미지 밖으로 삐져나와서는 계산이 되지 않는 것을 말한 것입니다. 그래서 Padding은 가장자리에도 필터를 적용하고자 해서, 이미지의 가장자리에 0같은 값으로 채워주는 것을 말합니다.
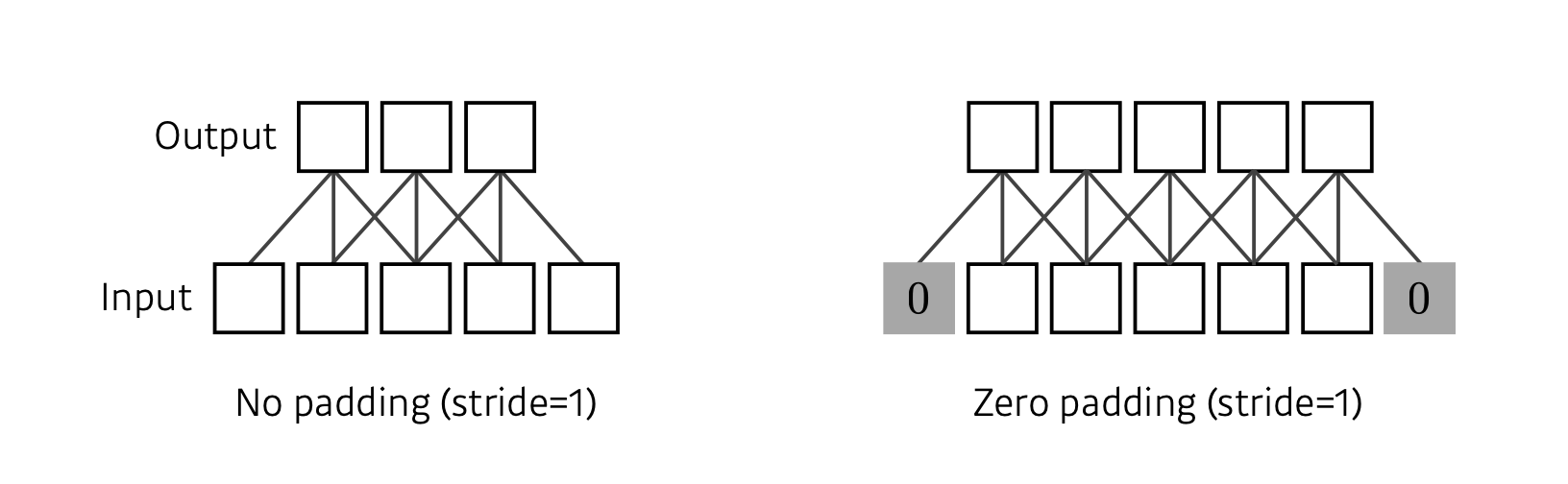
5 크기의 Input이 있을 때 3 크기의 필터가 있으면 출력은 3이 됩니다.
출력을 원래 Input 크기만큼의 5로 만들어 주려면 가장 자리에 0을 덧댐으로서 즉 0 Padding을 함으로써 5로 만들어 줄 수 있게 됩니다.
Stride&Padding
다음은 2차원 상에서 Stride 와 Padding을 다르게 하여 Convolution 연산을 도식화 한 것입니다.
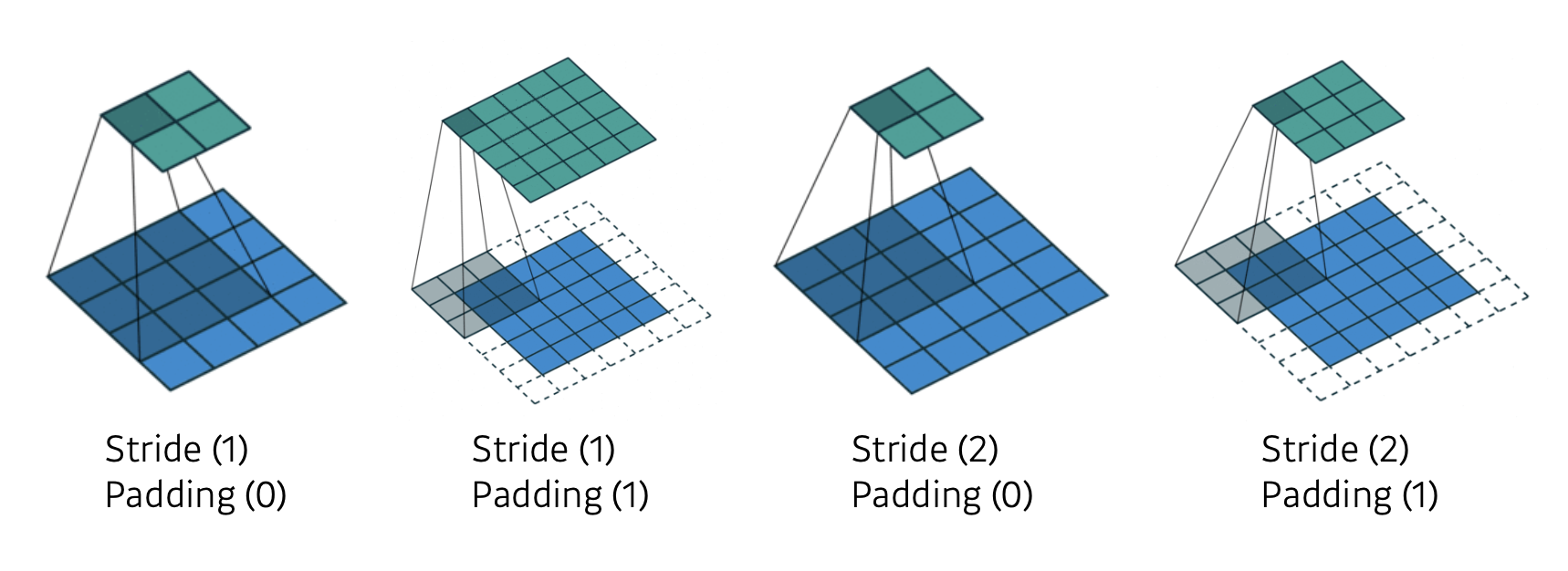
Convolution Arithmetic
밑의 그림을 보고 Convolution 연산이 될 때의 parameter 수를 계산해 봅시다.
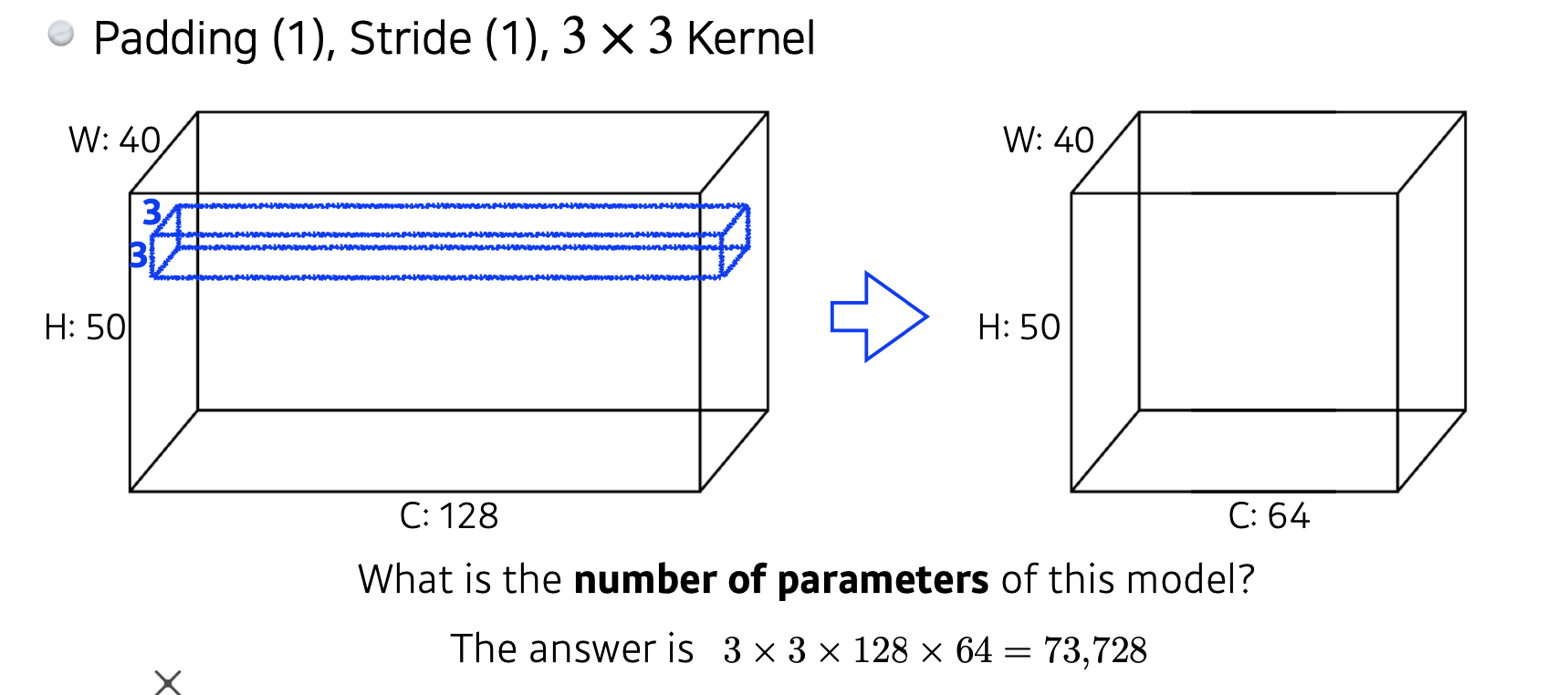
논문을 보거나 대부분의 자료에서 이렇게 도식화 된 그림을 많이 볼 수 있고, 도형 옆에는 각각 수들이 적혀 있습니다.
H: 세로 길이를 의미합니다.
W: 가로 길이를 의미합니다.
C: 채널 수, 깊이를 의미합니다. 보통 이미지라면 R, G, B의 3개의 값이고 투명도 까지 더해지면 4개의 값이 됩니다.
파란색 네모 박스는 왼쪽 큰 상자에 대해 적용할 필터가 됩니다.
3x3 크기의 필터를 적용하겠다는 것이고, 당연히 큰 상자의 채널 수와 필터의 채널 수는 일치해야 합니다.
그렇다면 필터의 패러미터 수는 3x3x128이 됩니다.
오른쪽의 출력의 채널 수는 64개가 되는데 이는, 오른쪽의 박스가 파란색 네모 필터를 64개 적용해서 얻어진 결과물이 됩니다. 왜냐하면 파란색 네모인 필터 하나 당 채널이 1인 feature map을 만들기 때문입니다.
그래서 총 패러미터의 수는 3x3x128x64가 됩니다.
References
- CNN - Convolution - 최성준 교수님

Leave a comment