베이즈 정리 / 딥러닝 입문 / MLP

베이즈 정리 / 딥러닝 입문/ MLP

베이즈 정리는 데이터가 새로 추가되었을 때 정보를 업데이트하는 방식에 대한 기반이 되므로 오늘날 머신러닝에 사용되는 예측모형의 방법론으로 굉장히 많이 사용되는 개념입니다.

베이즈 정리

베이즈 통계학을 이해하기 위해선 조건부확률의 개념을 이해해야 합니다.

조건부확률 P(A∣B)는 사건B가 일어난 상황에서의 사건A가 발생활 확률을 말합니다.

베이즈 정리는 조건부확률을 이용하여 정보를 갱신하는 방법을 알려줍니다.

베이즈 정리: 예제

COVID-99 의 발병률이 10% 로 알려져있다. COVID-99 에 실제로 걸렸을 때 검진될 확률은 99%, 실제로 걸리지 않았을 때 오검진될 확률이 1% 라고 할 때, 어떤 사람이 질병에 걸렸다고 검진결과가 나왔을 때 정말로 COVID- 99 에 감염되었을 확률은?

아래의 베이즈 정리 식을 이용하면 쉽게 구할 수 있습니다.

우리가 구하고자 하는 값은 어떤 사람이 질병에 걸렸다고 검진결과가 나왔을 때 정말로 COVID- 99에 감염되었을 확률이고 이는 바로 사후확률이 됩니다.

이 사후확률은 사전확률인 발병률이 10% * 가능도인 COVID-99 에 실제로 걸렸을 때 검진될 확률은 99% / Evidence 로 구할 수 있습니다.

Evidence는 다음과 같이 구할 수 있습니다.
질병에 결렸을 때, 검진될 확률 * 발병률 + 질병에 걸리지 않았을 때 검진될 확률(오진) * 발병률의 부정

따라서 위 값을들 조합해 계산해보면 아래와 같습니다.

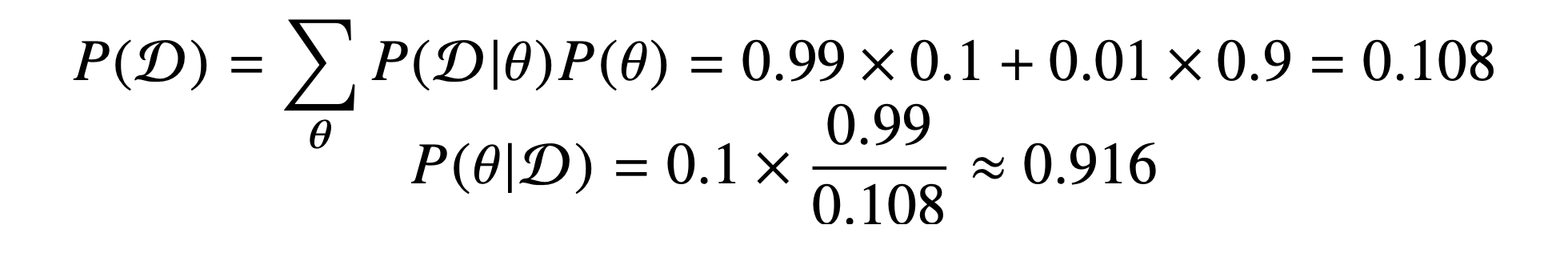
만약 오진률 즉, 발병되지 않았는데 검진될 확률이 0.1 = 10%로 올라간다면, Evidence에서의 값이 증가하게 되고 이는 사후 확률을 낮추게 됩니다.

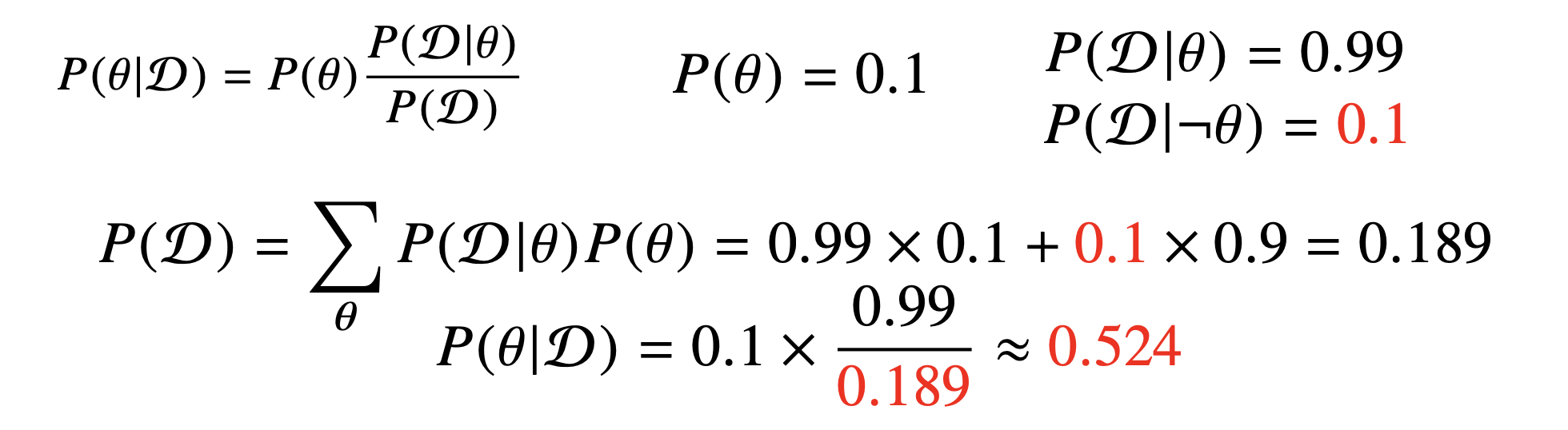
오진률이 높아짐으로 인해, 질병에 걸렸다고 검진결과가 나왔을 때, 실제로 그사람이 감염되었을 확률이 낮아진다는 것입니다.

베이즈 정리를 통한 정보의 갱신

베이즈 정리를 통해 새로운 데이터가 들어왔을 때 앞서 계산한 사후확률을 사전확률로 사용하여 갱신된 사후확률을 계산할 수 있습니다.

앞서 COVID-99 판정을 받은 사람이 두 번째 검진을 받았을 때도 양성이 나 왔을 때 진짜 COVID-99 에 걸렸을 확률은?

갱신된 evidence는 다음과 같이 계산 됩니다.

빨간색 텀이 바로 전 단계에서 계산한 사후확률이고 이것이 이번 단계에서의 사전 확률로 들어가게 되는 것입니다.

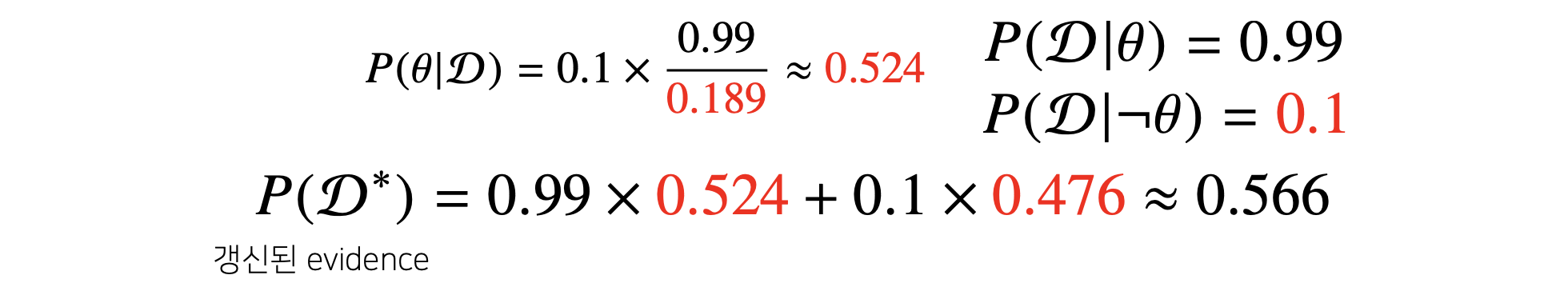
그리고 갱신된 사후확률은 다음과 같이 계산될 수 있습니다.

사전확률이 전 단계에서 계산된 값으로 들어가고 위에서 계산한 evidence값이 분모로 들어가게 됩니다.
나머지는 원래 계산하던 것과 마찬가지 입니다.

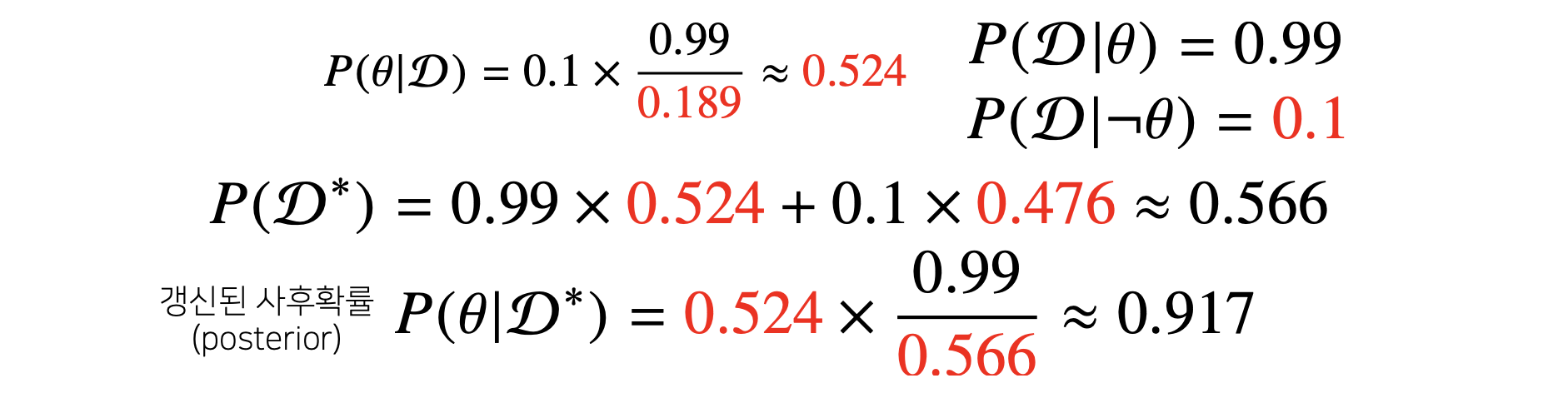
Deep Learning Basic

딥러닝에 대한 소개, 그리고 딥러닝의 역사에 대해 배웁니다.

CNN(Convolutional neural networks), RNN(Recurrent Neural Networks)와 같은 딥러닝 모델을 공부하기 전에 중요한 요소인 Data, Model, Loss, Optimization algorithms에 대해 배웁니다.

What make you a good deep learner ?

• 가지고 있는 아이디어나 논문의 이론을 실제로 구현할 수 있는 능력
• 딥러닝을 공부하고 연구하는데에 필요한 선형대수와 통계학 등..
• 현재 어떤 트렌드가 있고, 어떤 연구결과가 나왔는지 아는 것이 매우 중요하다

Contents

앞으로 배우게 될 내용

1. Historical Review - 딥러닝의 역사적 리뷰
2. Neural Networks & Multi-Layer Perceptron - 신경망과 다층 퍼셉트론
3. Optimization Methods - 최적화 방법 (드롭아웃, 규제 등)
4. Convolutional Neural Networks - 합성곱 신경망
5. Modern CNN
6. Computer Vision Applications - 컴퓨터 비전 응용
7. Recurrent Neural Networks
8. Transformer
9. Generative Models Part1 10.Generative Models Part2

AI / ML / DL

• AI - 사람의 지능을 모방하는 것
• ML - 어떤 문제를 품에 있어, 데이터를 통해 학습하는 분야
• DL - 사랑의 지능을 모방하면서, 데이터를 통해 학습하고, 그 안에 딥 뉴럴 네트워크를 사용하는 위 두개의 분야 안의 세부적인 분야

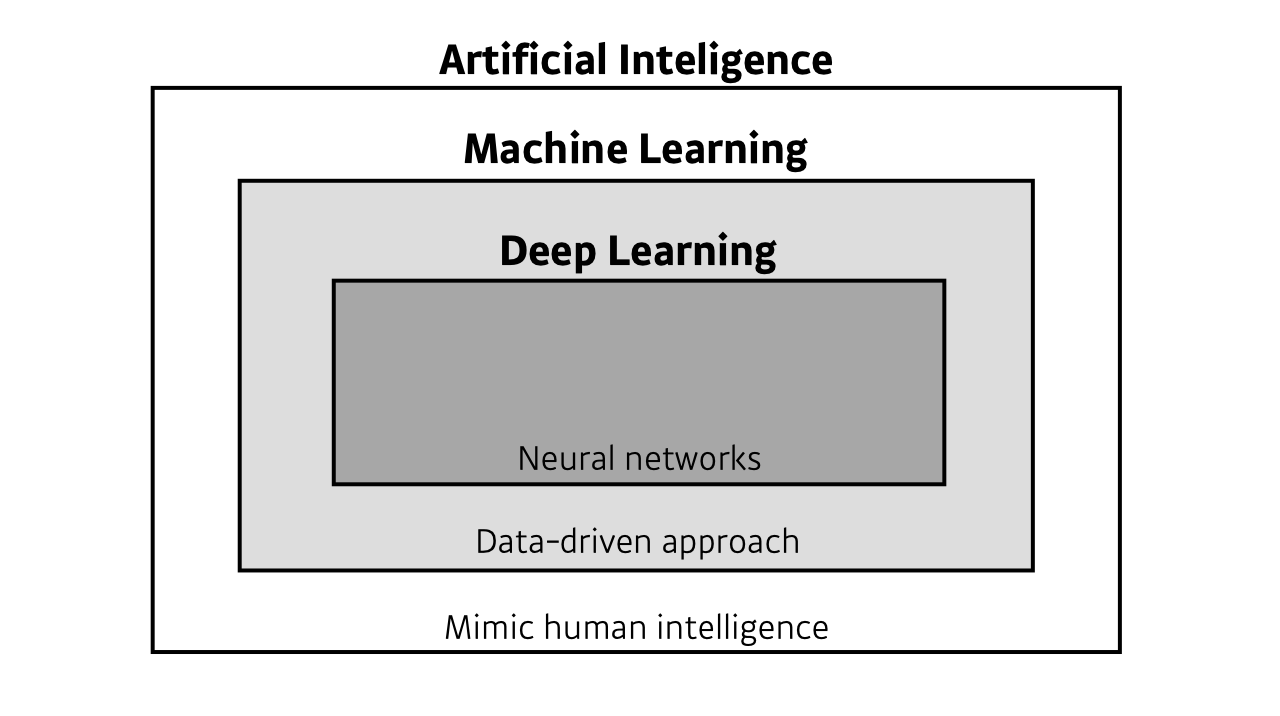
DL분야를 연구하는 것은 AI분야 전체를 연구한다는 것과는 동치가 아니다.

Key Components of Deep Learning

• The data that the model can learn from
• The model how to transform the data
• The loss function that quantifies the badness of the model
• The algorithm to adjust the parameters to minimize the loss

Data

• Data depend on the type of the problem to solve.
  데이터는 풀고자 하는 문제에 종속적이다.

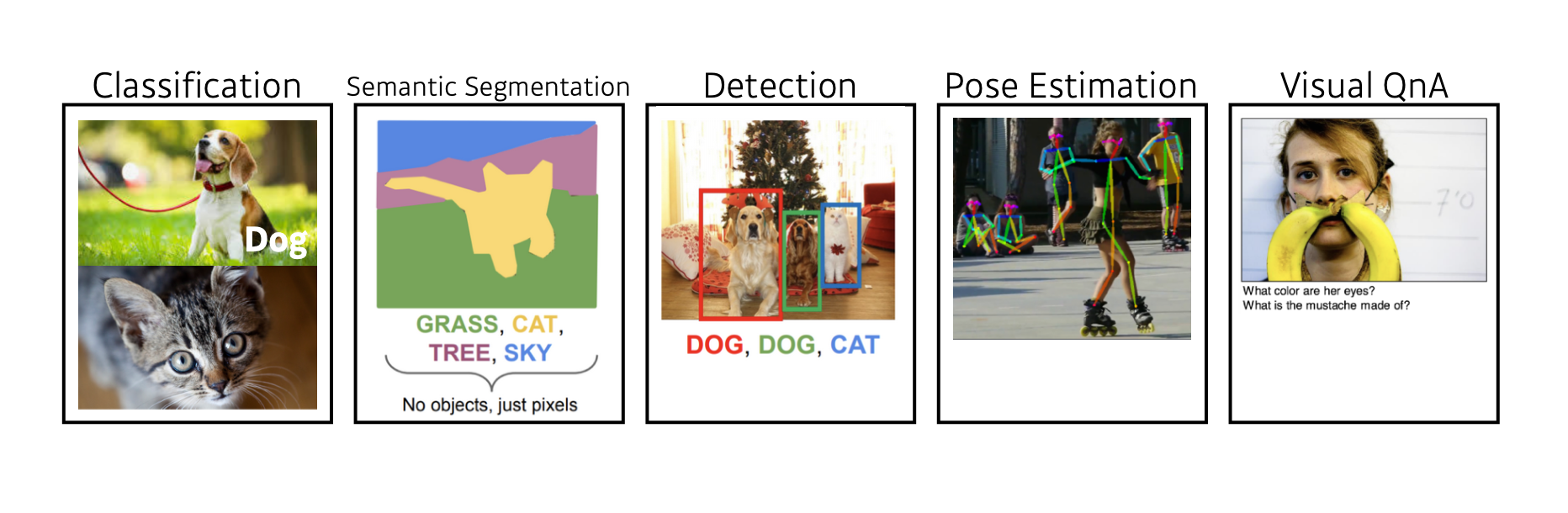
분류문제에서는 개와 고양이 같은 어떤 종류의 물체인지 분류하고, Semantic Segmentation같은 문제에서는 각 픽셀이 어디에 속하는 부분인지, Detection은 이미지에서 여러 종류의 물체가 있으면 이 물체의 바운더리에 어느 종류의 물체가 있는지 구분합니다.

Model

이미지, 텍스트 등이 주어졌을 때, 우리가 알고 싶어하는 문제의 예측값(레이블)을 도출해주는 역할을 한다.

문제에 따라 여러가지 모델이 존재하고, 성능도 각기 다르다.

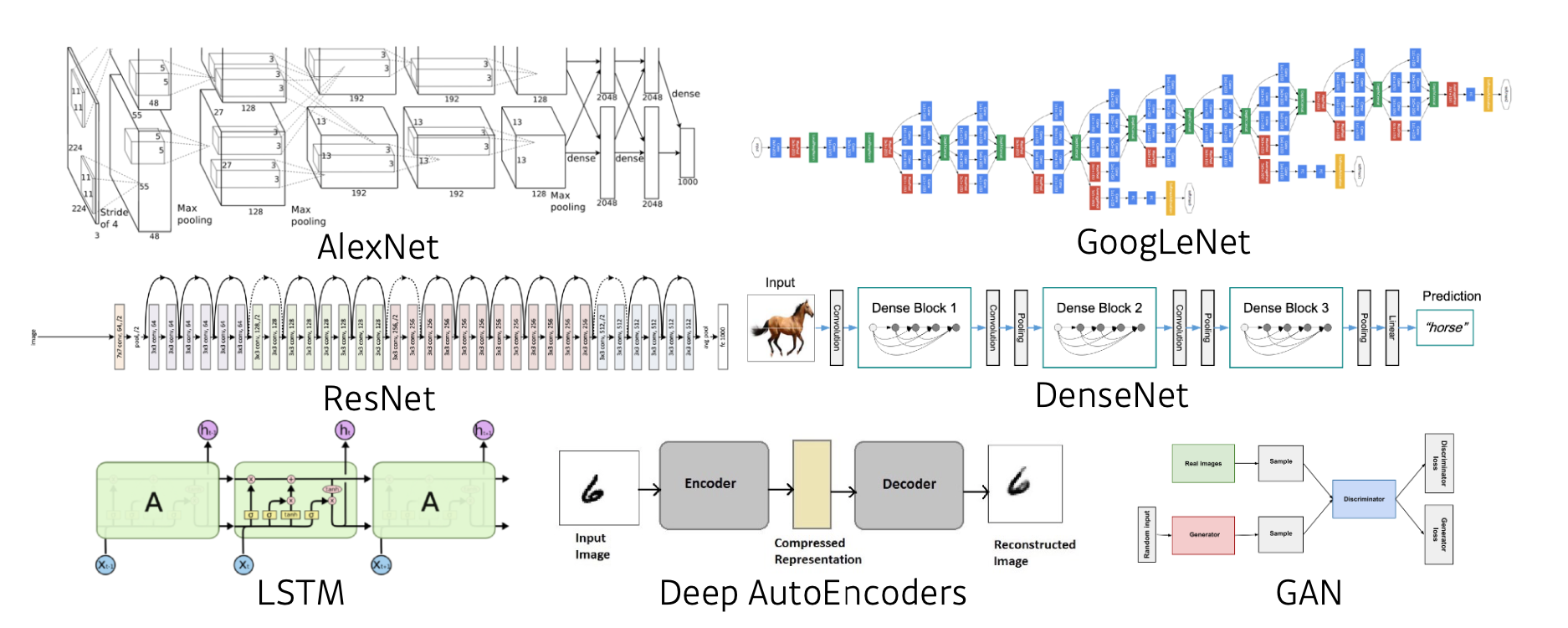
Loss

• The loss function is a proxy of what we want to achieve.
  문제에서 풀고 이루고자 하는 목적을 달성하기 위한 근사치

문제에 따라 적용되는 손실함수의 종류가 달라지게 된다.

전형적인 선형회귀 같은 문제에서는 예측값과 정답레이블 사이의 거리를 최소화 하기 위해 MSE(최소제곱오차)라든지, 분류문제에서는 여러개의 선택지 중 어느 것이 확률이 제일 높은지 예측하기 위해 CE(교차 엔트로피)같은 손실함수를 적용한다.

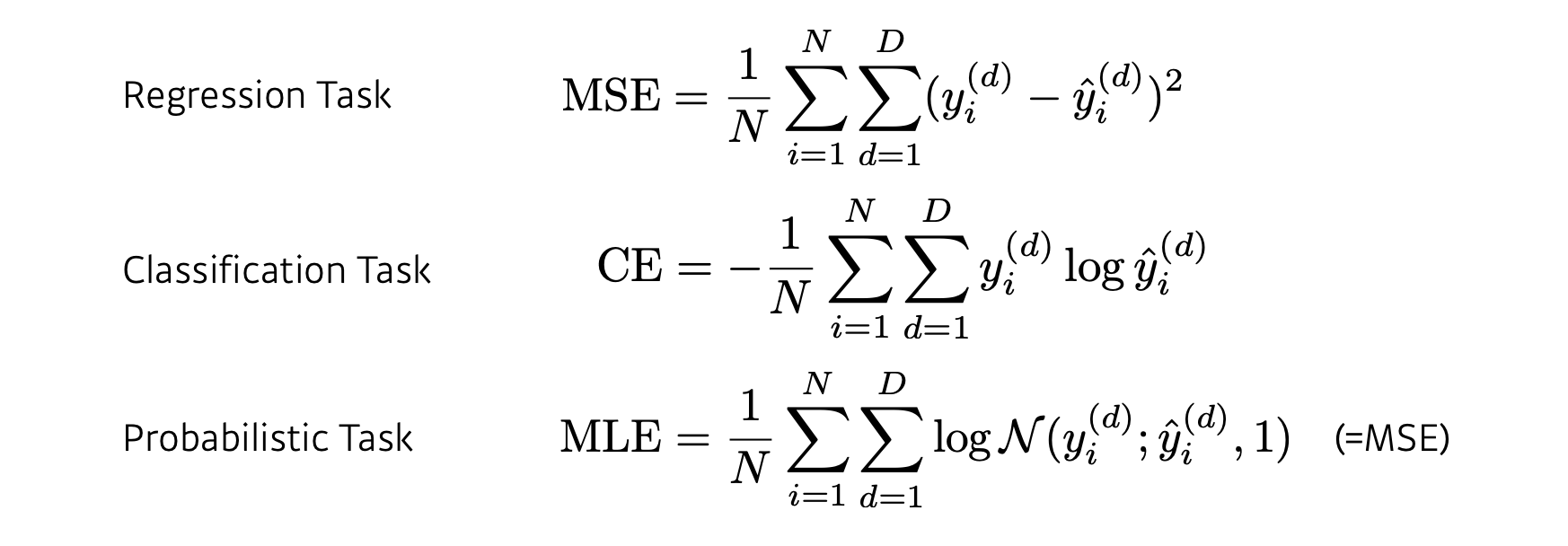
Optimization Algorithm

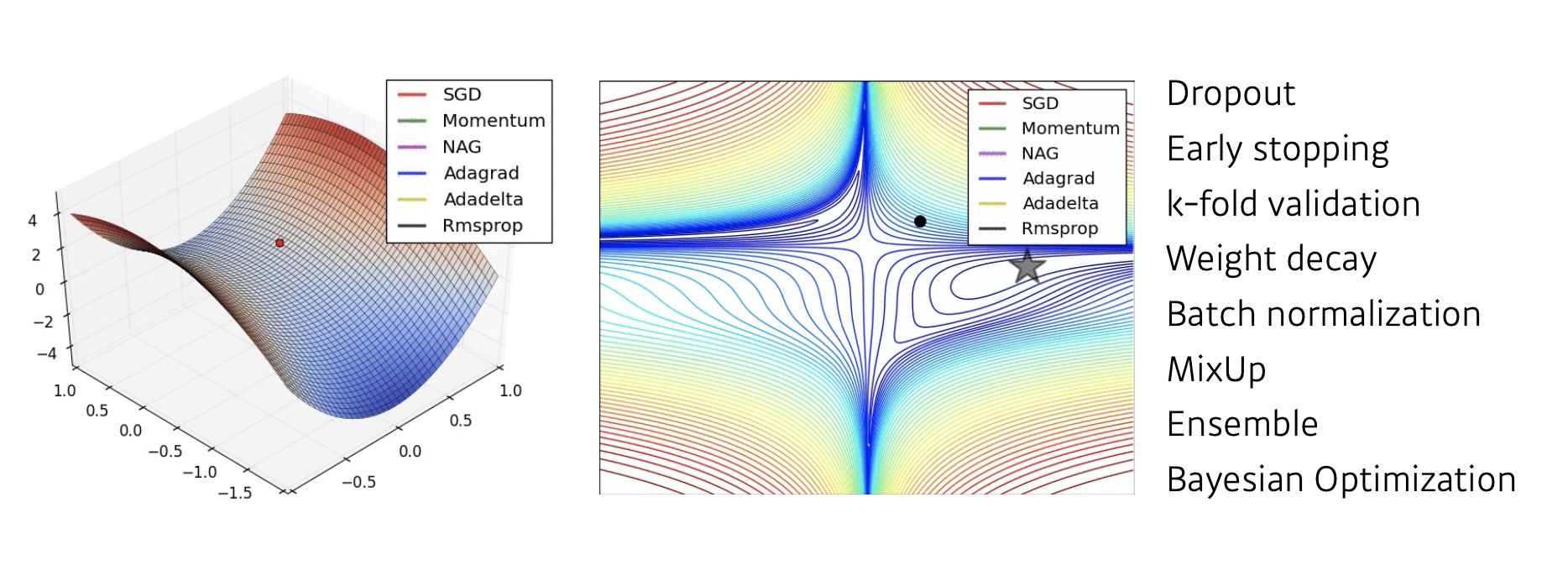
퀴즈 정리

1. 다음의 식이 성립하는가?

   P(A∩B)=P(A)P(B∣A)

   기본적인 조건부 확률 문제로서, P(B∣A)는 사건 A가 일어났을 때, B가 일어날 확률을 의미합니다.

2. 사후확률 (posterior) 은 가능도 (likelihood) 에 반비례하는가?

   가능도는 사후확률에 비례하고, Evidence가 반비례하게 됩니다.

3. 다음의 식이 성립하는가?

   P(A∣B) = P(A)P(B∣A)/P(B)

   양변에 P(A)를 곱해주면 식은 성립하게 됩니다.

4. A가 binary variable일 때, 다음의 식이 성립하는가?

   P(A∣B) = P(B∣A)P(A) / P(B∣A)P(A)+P(B∣¬A)P(¬A)

   이항변수일 때의 베이즈 정리의 공식을 묻는 문제였습니다.

5. 모든 변수에 대한 조건부 확률만으로 인과관계를 추론할 수 있는가?

   인과관계를 추론함에 있어 어떤 중첩효과가 있는지 연구 후에 이를 제거해야 올바른 추론이 가능합니다.

References

• Mathematics for Artificial Intelligence - Unist 임성철 교수님
• Deep Learning Basic - 최성준 교수님