판다스 / 딥러닝에서의 확률론 기본
판다스는 구조화된 데이터의 처리를 지원하는 Python 라이브러리입니다.
고성능 array 계산 라이브러리인 numpy와 통합하여, 강력한 “스프레드시트” 처리 기능을 제공하므로 Data science 분야에서 널리 쓰이는 판다스를 알아봅니다.
저번 포스팅에 이어, pandas 라이브러리 기능에 대해 알아봅니다.
딥러닝의 왜 확률론이 필요한지 알아봅니다.
데이터의 초상화로써 확률분포가 가지는 의미와 이에 따라 분류될 수 있는 이산확률변수, 연속확률변수의 차이점, 확률변수, 조건부확률, 기대값 등에 대해 알아봅니다.
pandas - groupby
특정 조건에 맞는 데이터들을 묶을 수 있는 기능입니다.
- SQL groupby 명령어와 같음
- split -> apply -> combine 과정을 거쳐 연산함
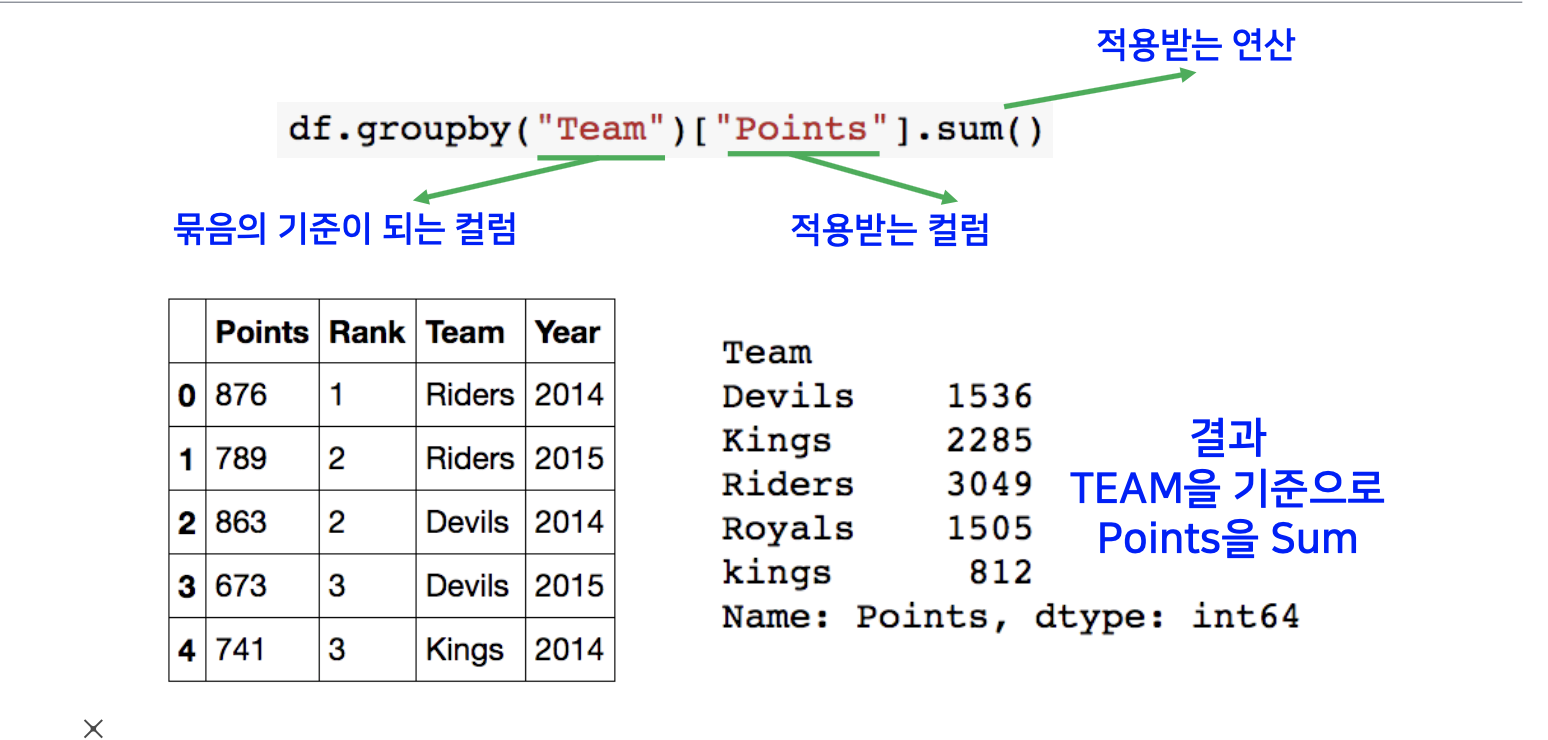
그룹바이 함수에는 묶음의 기준이 되는 컬럼이 들어가고 뒤에 적용하고자 하는 연산에 해당되는 컬럼을 입력합니다.
결과는 팀을 기준을 한 point들을 모두 합한 시리즈가 출력이 됩니다.
아래 그림 처럼 한 개 이상의 column을 묶을 수도 있습니다.
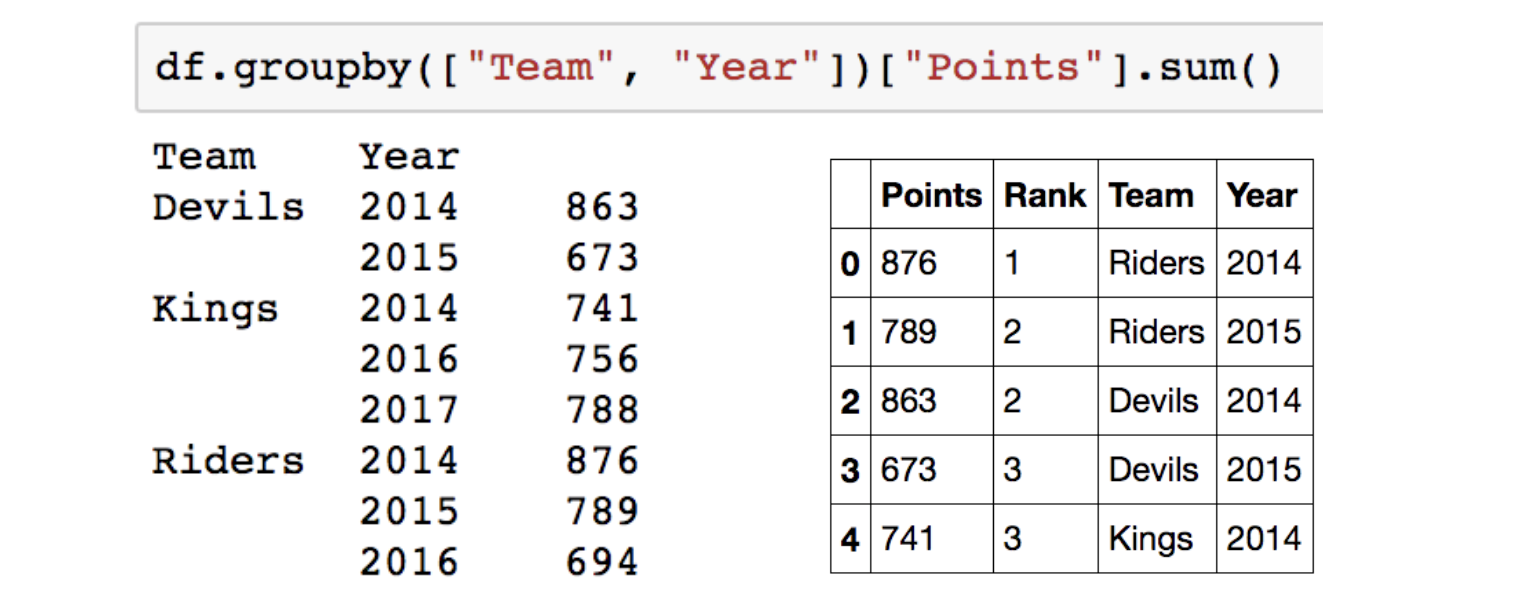
Hierarchical index
- Groupby 명령의 결과물은 dataframe 입니다.
- 두 개의 column으로 groupby를 할 경우, index가 두개 생성됩니다.
- 아래의 그림에서는 ‘Team’과 ‘Year’의 인덱스가 생성된 모습입니다.
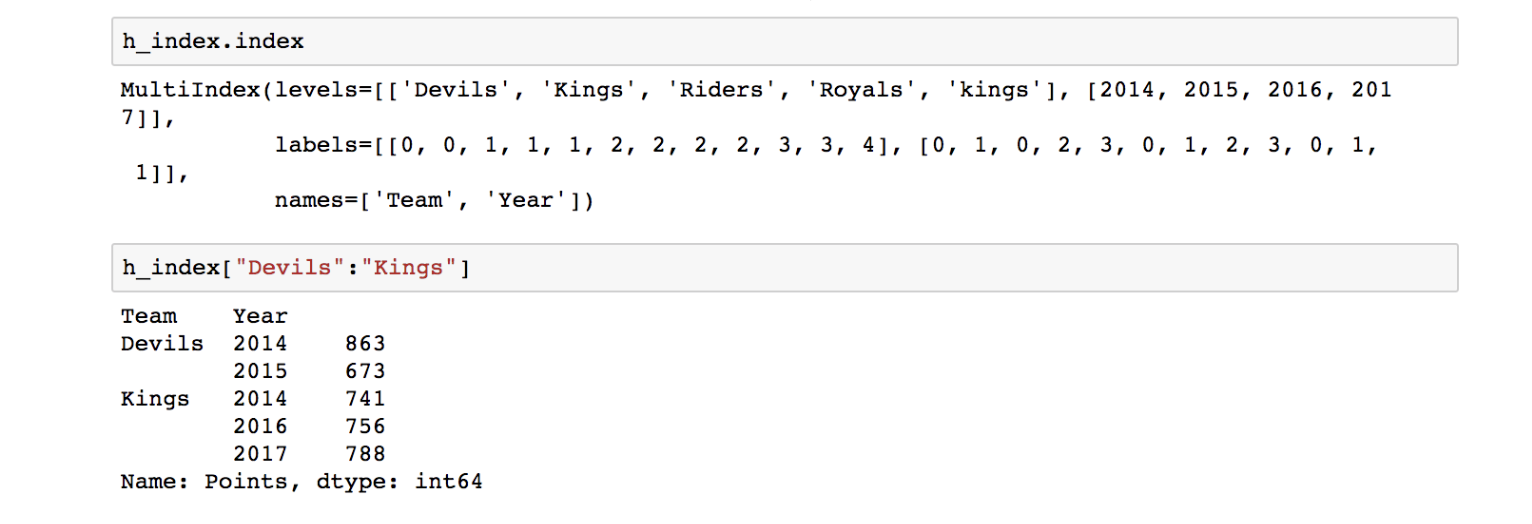
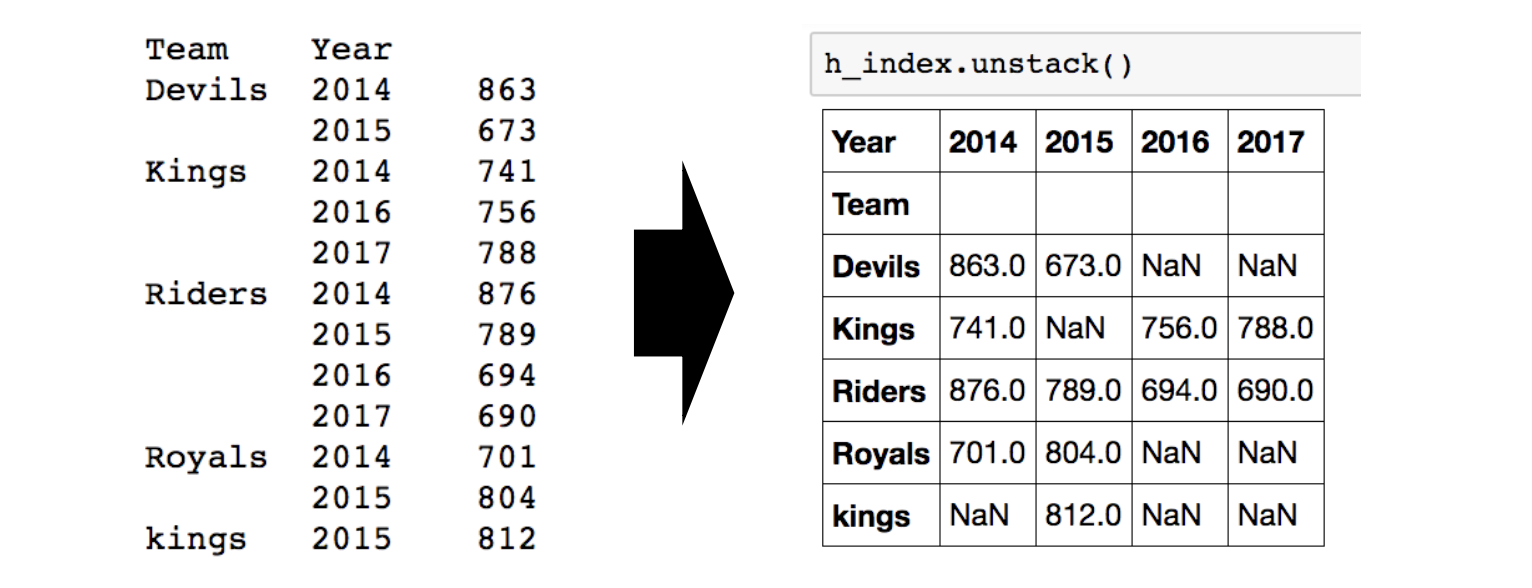
Hierarchical index – unstack()
Group으로 묶여진 데이터를 matrix 형태로 전환해주는 기능입니다.
Hierarchical index – operations
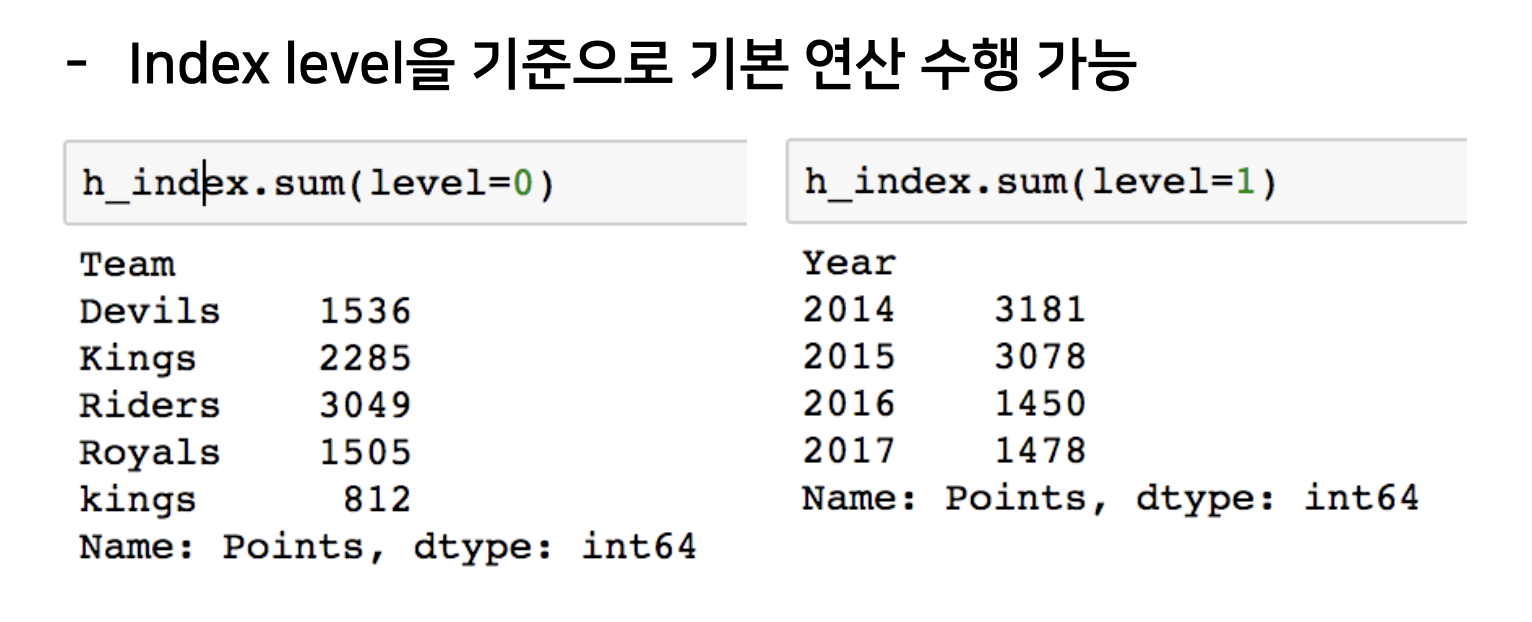
Index level을 기준으로 주어진 기본 연산이 수행 됩니다.
밑의 그림에서 level 0은 Team이고, level2는 Year 입니다.
Groupby – gropued
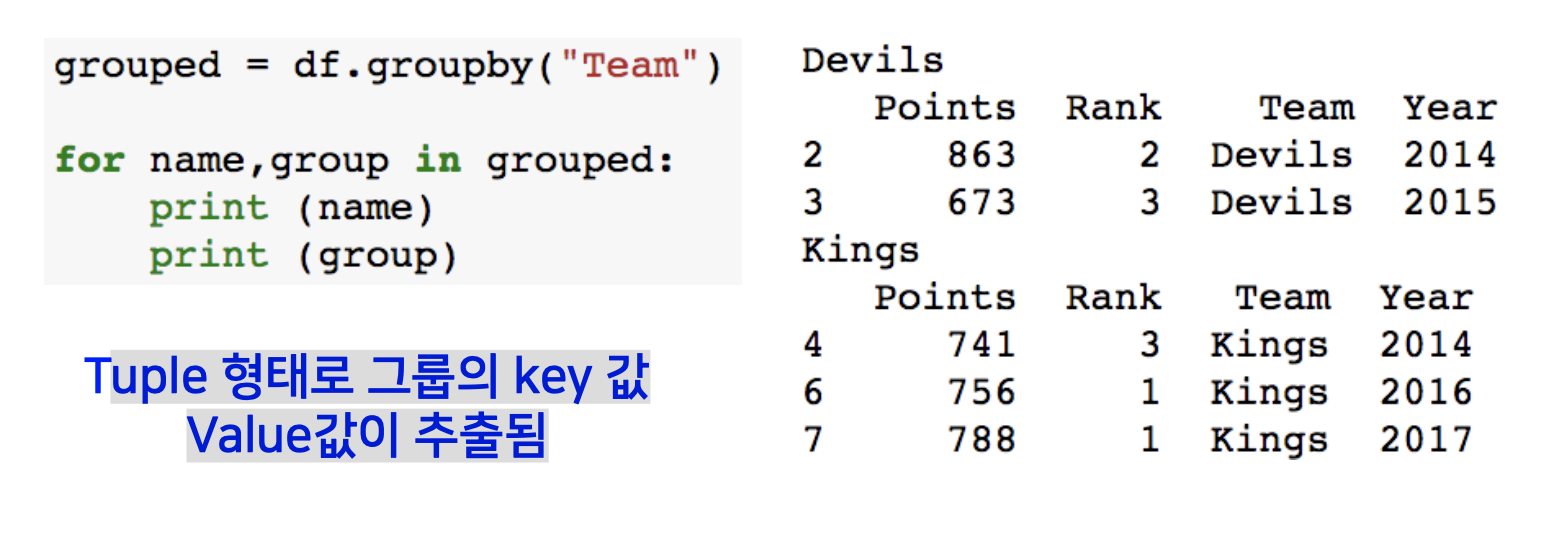
Groupby에 의해 Split된 상태를 추출 가능합니다.
Tuple 형태로 그룹의 key 값 Value값이 추출됩니다.
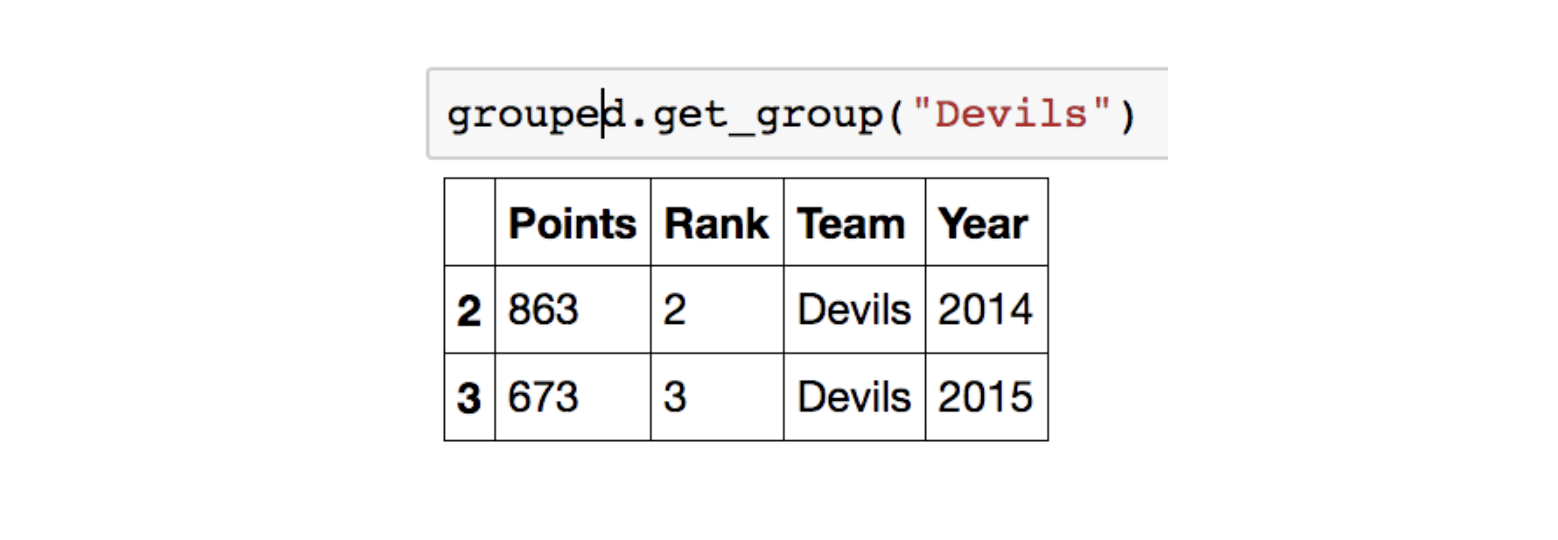
특정 key값을 가진 그룹의 정보만 추출도 가능합니다.
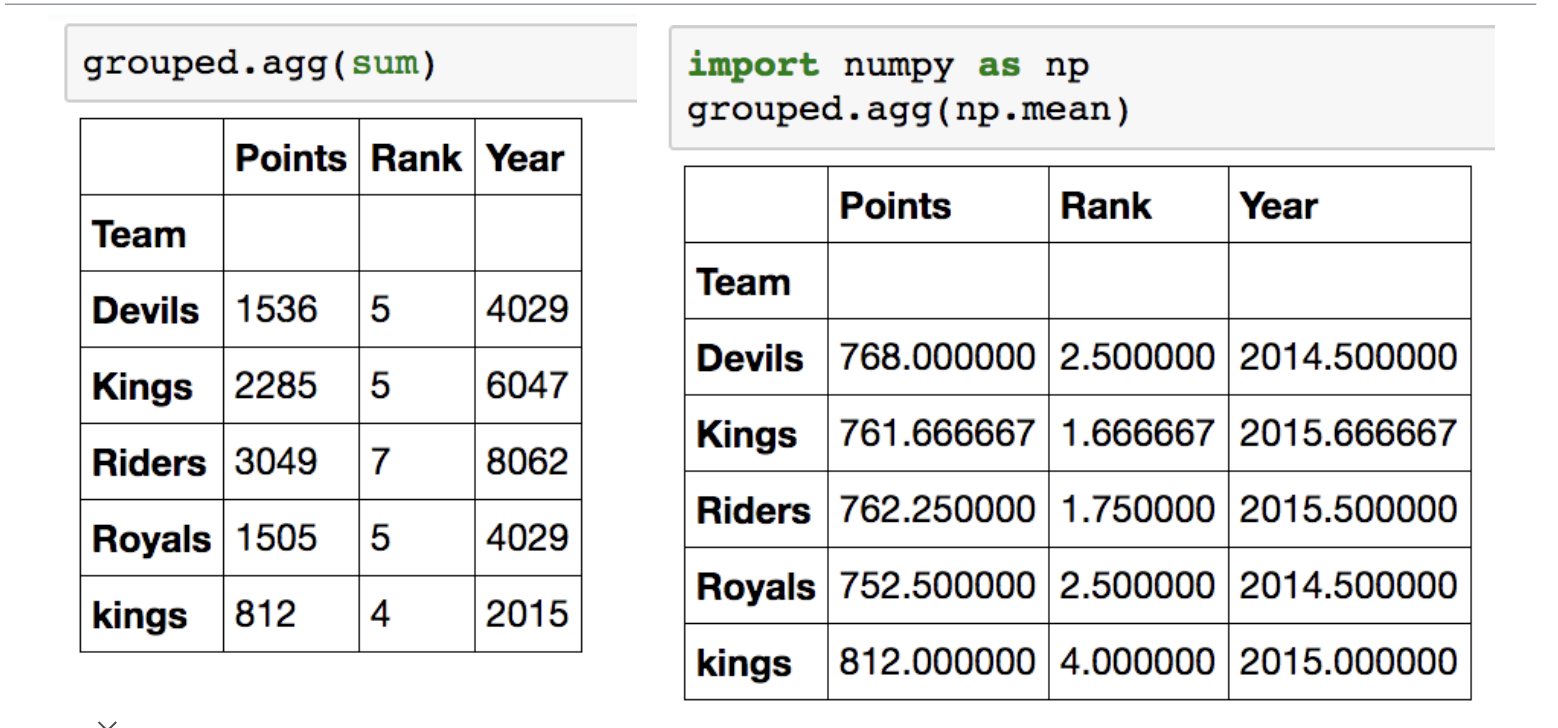
Groupby – aggregation
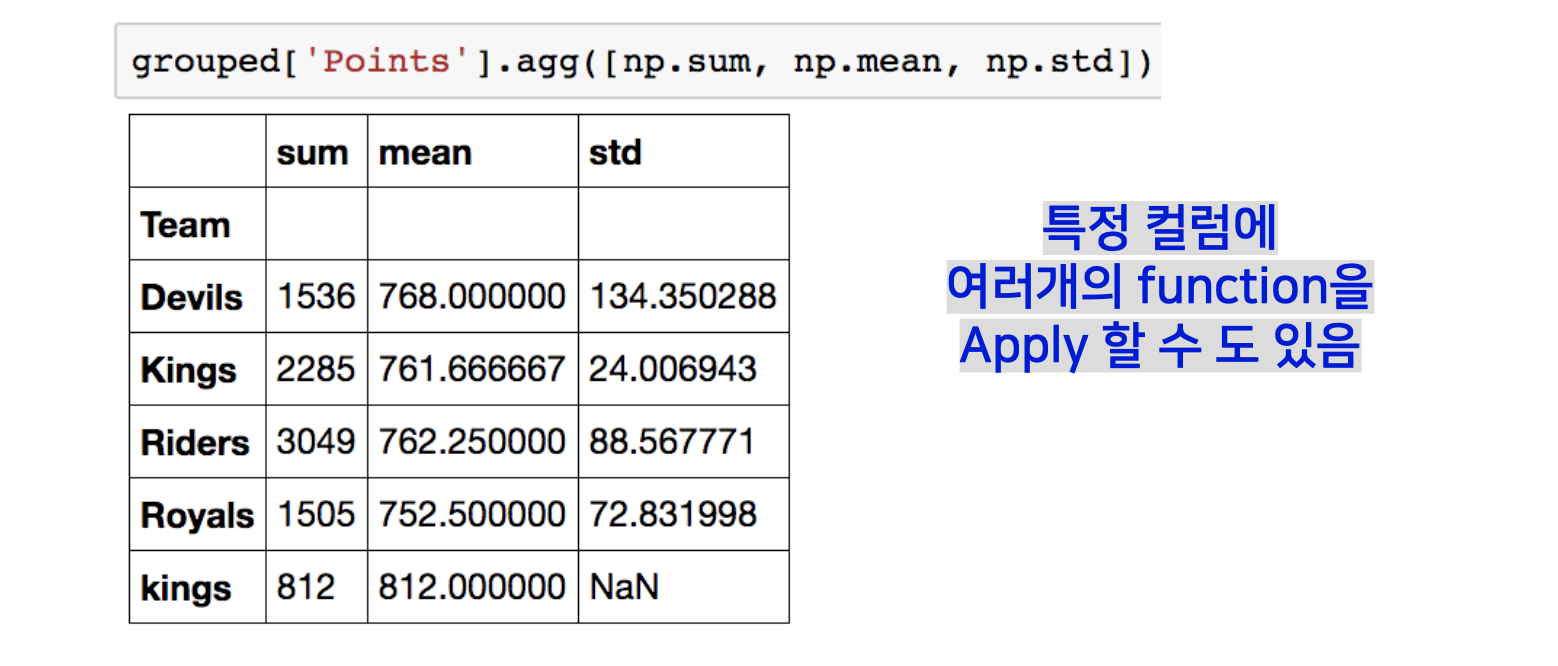
추출된 group 정보에 Aggregation이라는 요약된 통계정보를 추출해 줄 수 있는 기능을 적용할 수 있습니다.
특정 컬럼에 여러개의 function을 Apply 할 수 도 있습니다.
Groupby – transformation
Transformation은 Aggregation과 달리 key값 별로 요약된 정보가 아니고 개별 데이터의 변환을 지원합니다.
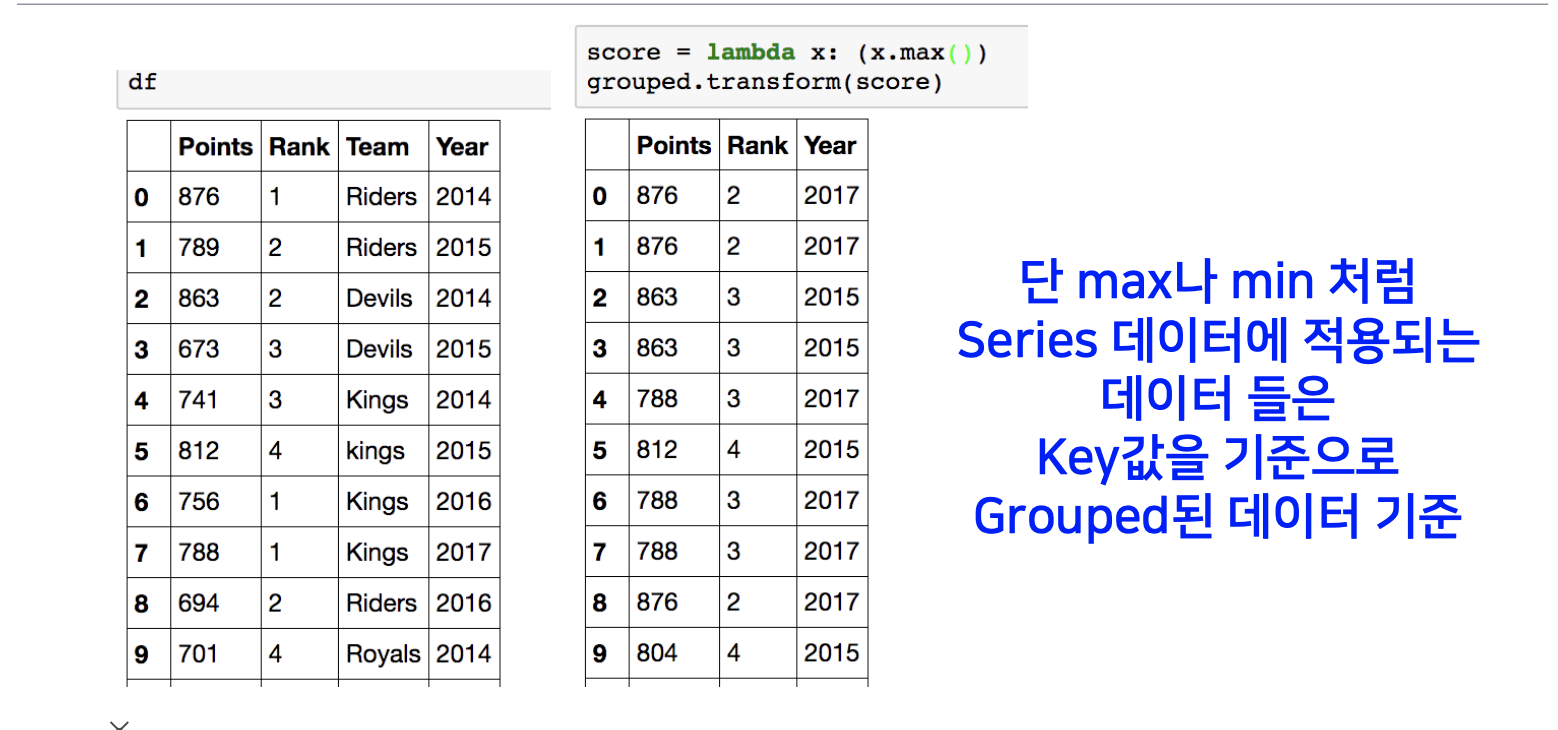
전체 그룹에서 칼럼 별로 가장 큰 값을 뽑아서, 그 값으로 전체 각각의 그룹의 칼럼 별 데이터를 갱신합니다.
Merge & Concat
Merge는 SQL에서 많이 사용하는 Merge와 같은 기능으로써, 두개의 데이터를 하나로 합치는 기능입니다.
같은 칼럼 네임을 갖고 있는 데이터 프레임이 두개가 있고, ‘subject_id’의 같은 칼럼 값으로 merge를 하면 다음 그림과 같이 됩니다.
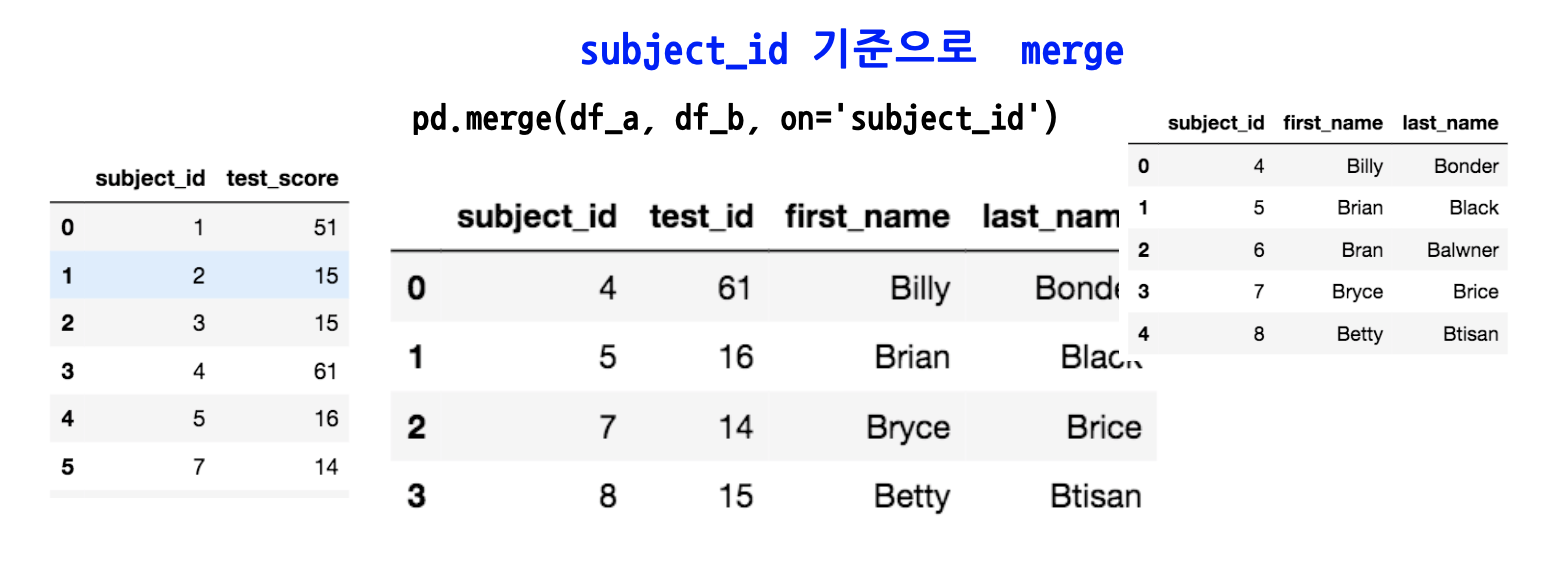
합병의 기준이 되는 컬럼의 이름이 다를 땐 ‘left_on’, ‘right_on’ 옵션을 각각 지정해주면 됩니다.
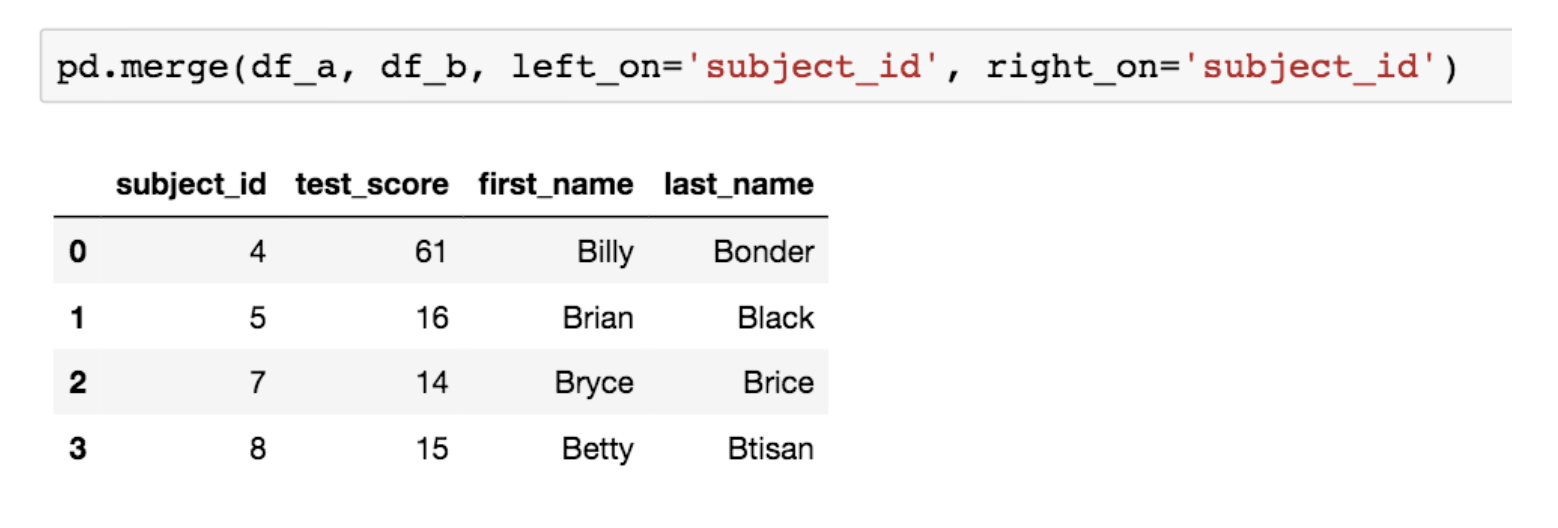
SQL을 하신 분이라면 익숙한 그림입니다.
Merge는 어느 방법을 쓰느냐에 따라, 다음과 같이 도식화 될 수 있습니다.
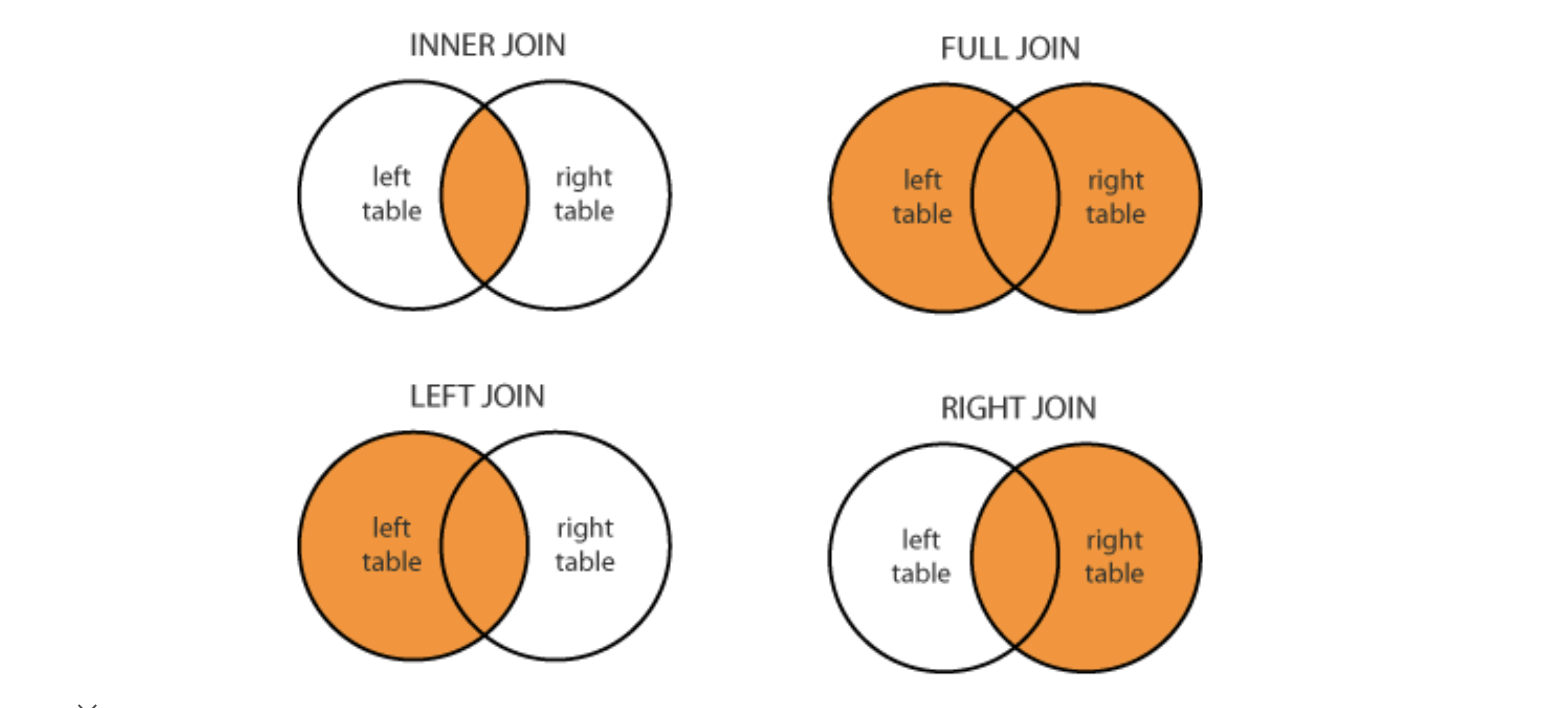
Merge example
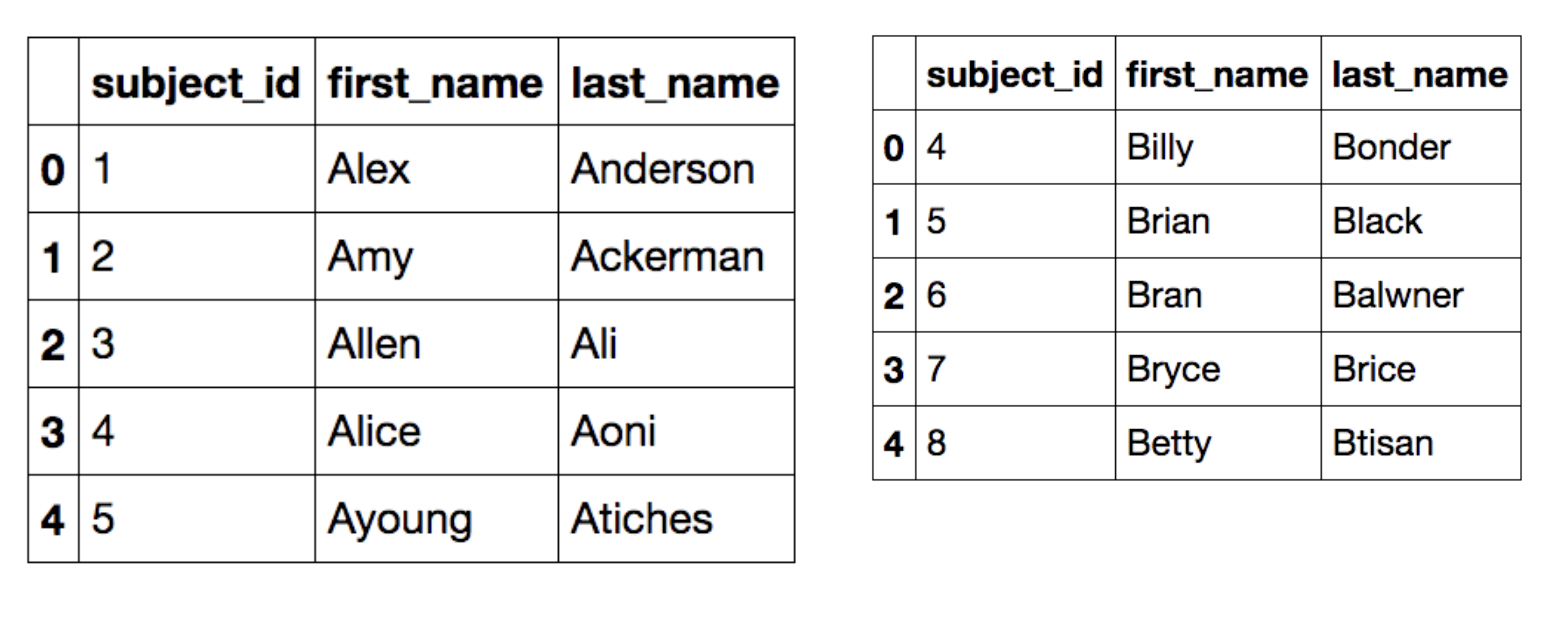
다음은 예제에 사용될 데이터 프레임들 입니다.
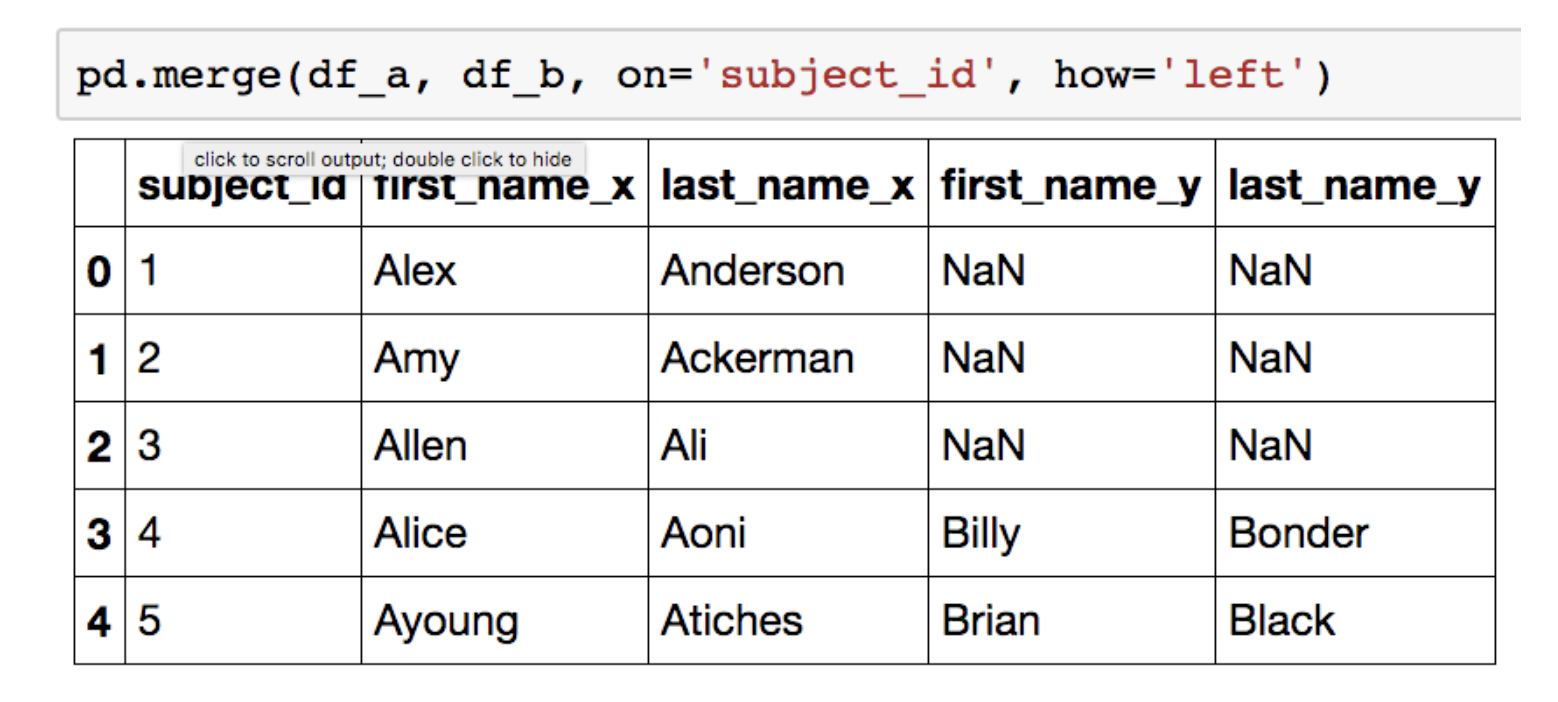
left join
subject_id가 기준이 되면서, 왼쪽에 있는 모든 데이터도 머지 대상이 됩니다.
오른쪽 데이터에서 왼쪽 데이터의 칼럼에 해당되지 않는 부분은 NaN값으로 채워집니다.
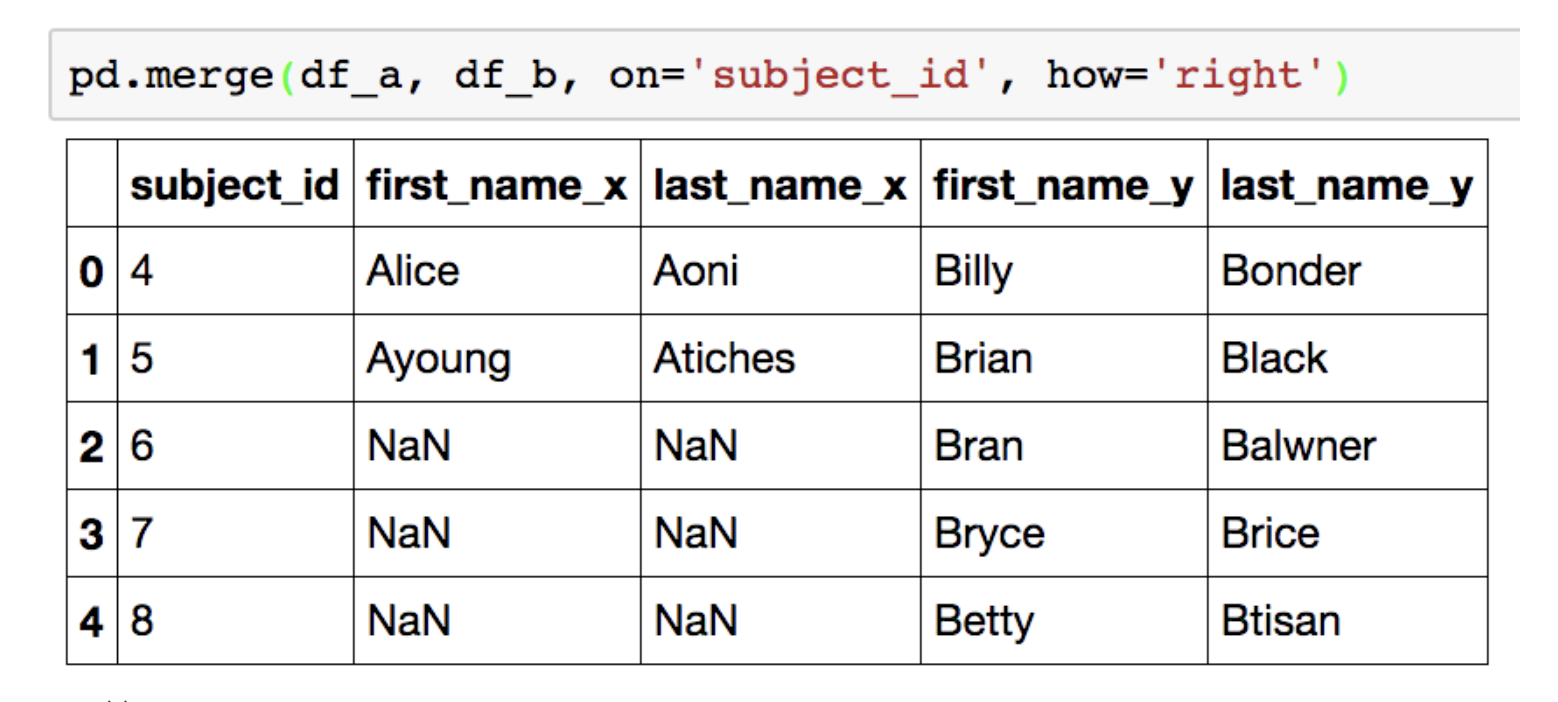
right join
subject_id가 기준이 되면서, 오른쪽에 있는 모든 데이터도 머지 대상이 됩니다.
왼쪽 데이터에서 오른쪽 데이터의 칼럼에 해당되지 않는 부분은 NaN값으로 채워집니다.
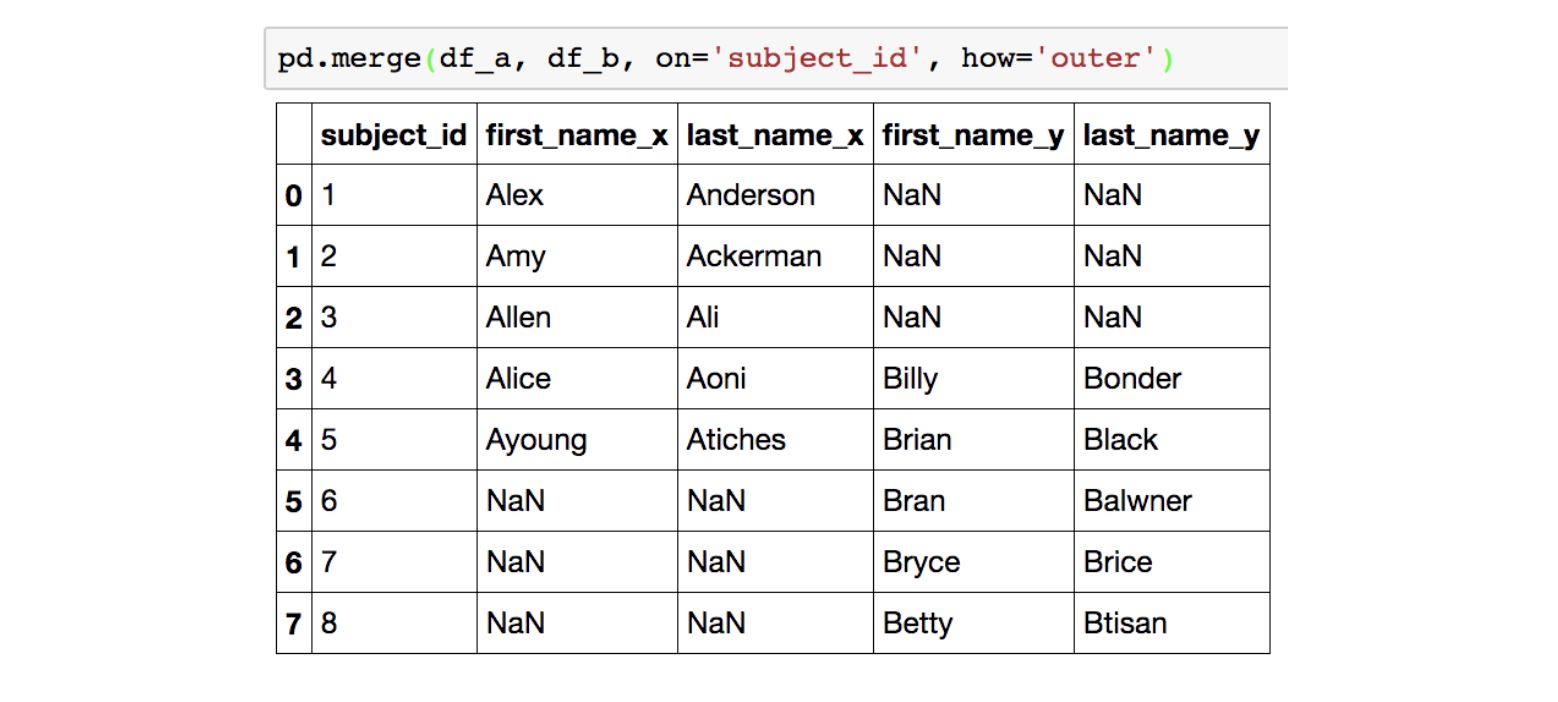
full(outer) join
subject_id가 기준이 되면서, 양쪽에 있는 모든 데이터가 머지 대상이 됩니다.
왼쪽 데이터에서 오른쪽 데이터의 칼럼에 해당되지 않는 부분 그리고 오른쪽 데이터에서 왼쪽 데이터의 칼럼에 해당되지 않는 부분은 NaN 값으로 채워집니다.
Concat
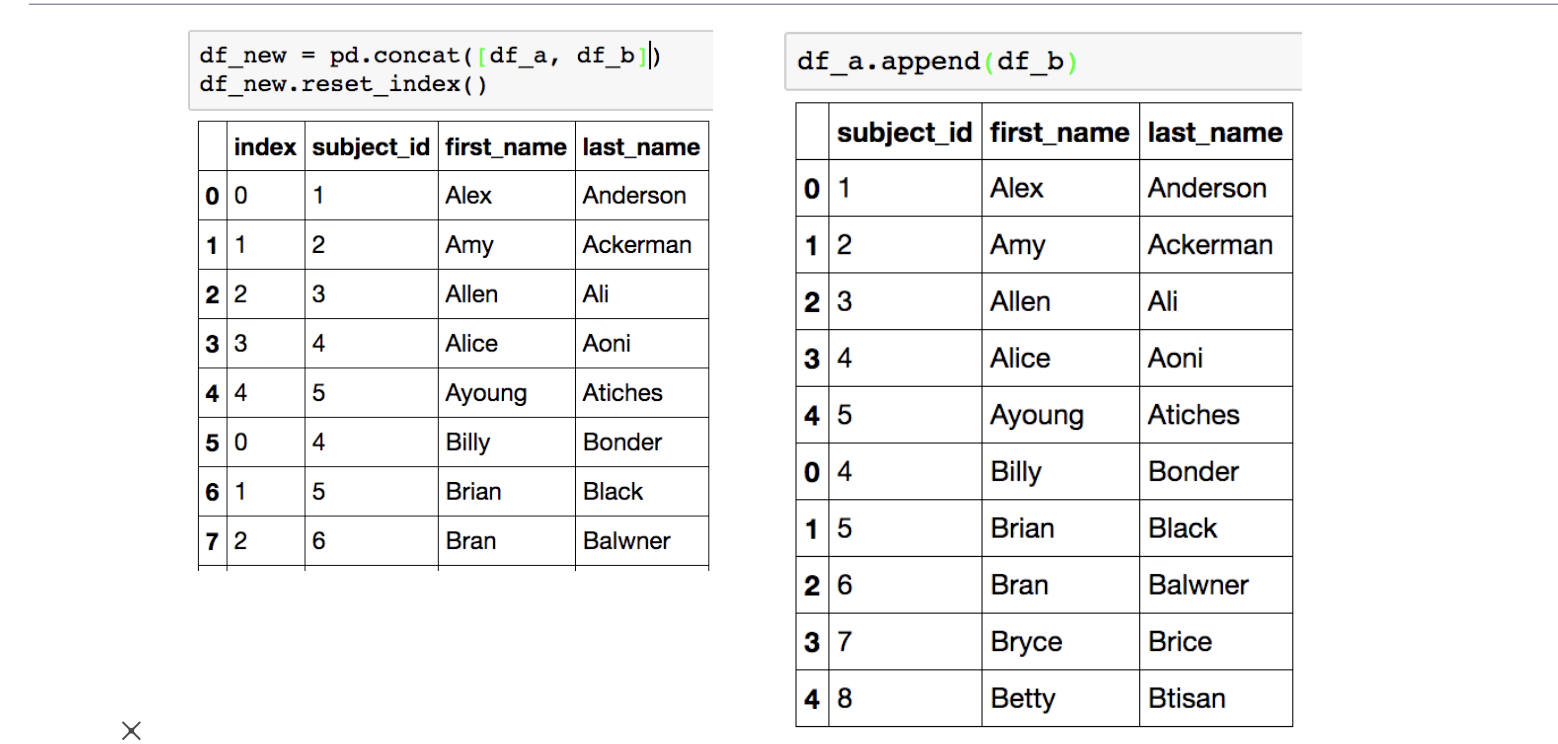
말그대로, 같은 형태의 데이터를 붙이는 연산작업 입니다.
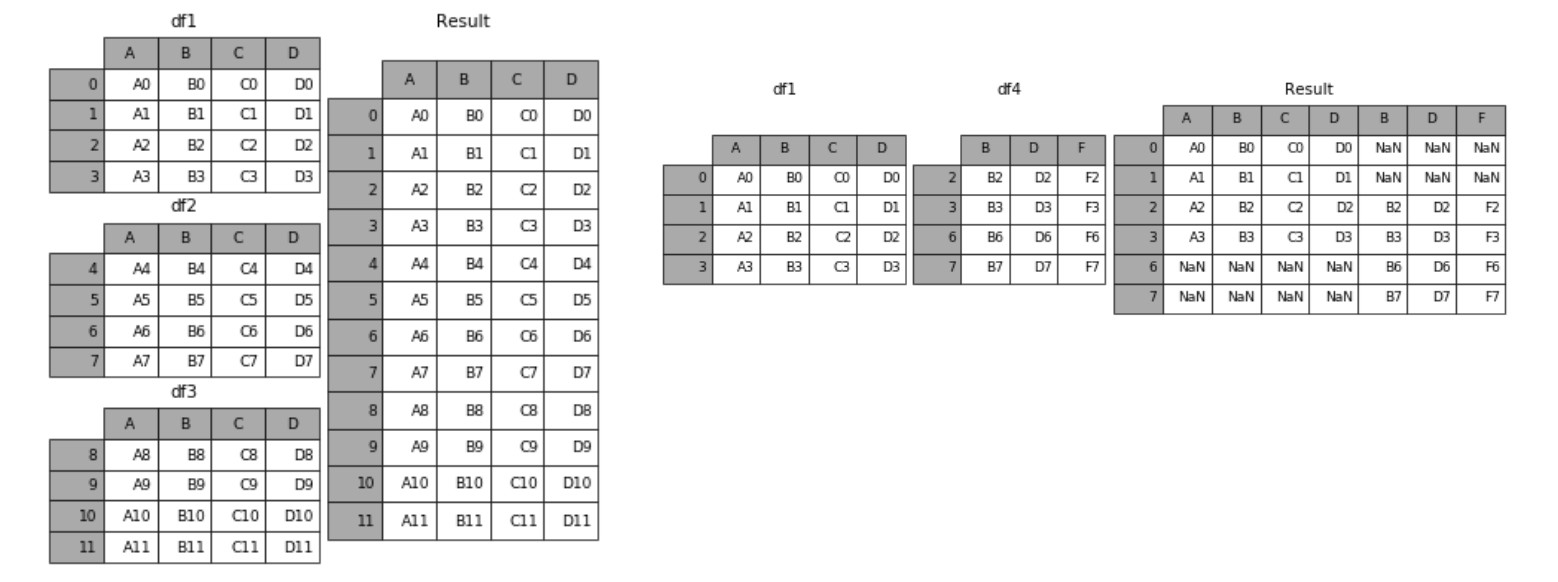
pd.concat([df1, df2])과 `df1.append(df2) 방식이 있습니다.
딥러닝 확률론
딥러닝에서 확률론이 왜 필요한가요?
딥러닝은 확률론 기반의 기계학습 이론에 바탕을 두고 있습니다. 기계학습에서 사용되는 손실함수(loss function)들의 작동 원리는 데이터 공간을 통계적으로 해석해서 유도하게 됩니다. (예측이 틀릴 위험(risk)을 최소화하도록 데이터를 학습하는 원리는 통계적 기계학습의 기본 원리)
회귀 분석에서 손실함수로 사용되는 L2-노름은 예측오차의 분산을 가장 최소화하는 방향으로 학습하도록 유도합니다.
분류 문제에서 사용되는 교차엔트로피(cross-entropy)는 모델 예측의 불확실성을 최소화하는 방향으로 학습하도록 유도합니다.
분산 및 불확실성을 최소화하기 위해서는 측정하는 방법을 알아야하는데, 두 대상을 측정하는 방법을 통계학에서 제공하기 때문에 기계학습을 이해하려면 확률론의 기본 개념을 알아야 합니다.
이산확률변수 vs 연속확률변수
확률변수는 확률분포 𝒟 에 따라 이산형(discrete)과 연속형(continuous) 확률변수로 구분하게 됩니다.
이산형 확률변수는 확률변수가 가질 수 있는 경우의 수를 모두 고려하여 확률을 더해서 모델링합니다.
$P(X \in A) = \Sigma_{x \in A} P(X = x)$
연속형 확률변수는 데이터 공간에 정의된 확률변수의 밀도(density) 위에서의 적분을 통해 모델링합니다.
$P(X \in A) = \int_A P(x)dx$
조건부확률과 기계학습
조건부확률 $P(y \mid x)$는 입력변수 $x$ 에 대해 정답이 $y$ 일 확률을 의미합니다.
로지스틱 회귀에서 사용했던 선형모델과 소프트맥스 함수의 결합은 데이터에서 추출된 패턴을 기반으로 확률을 해석하는데 사용됩니다.
분류 문제에서 softmax$(W\phi + b)$은 데이터 $x$ 로부터 추출된 특징패턴 $\phi(x)$ 과 가중치행렬 $W$을 통해 조건부확률 $P(y \mid x)$을 계산합니다.
회귀 문제의 경우 조건부기대값 $𝔼[y \mid x]$ 을 추정합니다.
딥러닝은 다층신경망을 사용하여 데이터로부터 특징패턴 $\phi$을 추출합니다
기대값이 뭔가요?
확률분포가 주어지면 데이터를 분석하는 데 사용 가능한 여러 종류의 통계 적 범함수(statistical functional)를 계산할 수 있습니다.
기대값(expectation)은 데이터를 대표하는 통계량이면서 동시에 확률분포를 통해 다른 통계적Z 범함수를 계산하는데 사용됩니다.
$E_{x~P(x)}[f(x)] = \int_X f(x)P(x)dx$, $E_{x~P(X)}[f(x)] = \sum_{x \in X} f(x)P(x)$
피어세션 정리
오늘은 판다스의 그룹핑에 대한 내용과 딥러닝에서 왜 통계학이 중요하고 사용되는지에 대해 배울 수 있었는데, 오늘 내용 중 통계학 부분의 설명이 좀 난해하고 낯설다는 분이 많이 계서서, 다 같이 어느부분이 이해가 안되고 궁금한지 이야기하는 시간을 가질 수 있었습니다.
그리고 2주차 들어오면서 수학적인 내용을 다룸에 따라 하루의 마무리인 학습정리를 할 때, 블로그나 다른 매체에 수식을 입력할 수 있는 LaTex라는 문법에 대해 이야기 하였고, 이를 어떻게 하면 효율적으로 배우고 쓸 수 있을지에 대해 이야기해볼 수 있었습니다.
퀴즈 정리
-
이산형 확률변수는 확률변수가 가질 수 있는 경우의 수를 모두 고려하여 확률을 더해서 모델링한다?
확률변수가 가질 수 있는 경우의 수를 모두 고려하여 확률을 더해서 모델링하게 됩니다.
-
연속형 확률변수의 한 지점에서의 밀도(density)는 그 자체로 확률값을 가진다?
밀도는 누적확률분포에서의 확률이 아니라 변화율을 의미하게 됩니다.
-
몬테카를로 샘플링 방법은 변수 유형 (이산형, 연속형)에 상관없이 사용할 수 있다?
상관없이 사용할 수 있습니다.
-
각 면이 나올 확률이 균등하고 독립적인 정육면체 주사위를 던진다고 하자. 확률변수 $X$ 는 주사위의 각 면의 숫자를 나타낸다고 할 때 $(X \in {1, 2, 3, 4, 5, 6})$, $X$ 의 기대값을 구하시오 (소수점 첫째자리까지 입력).
각 확률변수에 확률함수 값을 곱하여 모두 더하면 되는 문제였습니다.
-
각 면이 나올 확률이 균등하고 독립적인 정사면체 주사위를 던진다고 하자. 확률변수 $X$ 는 주사위의 각 면의 숫자를 나타낸다고 할 때 $(X \in {1, 3, 5, 7})$, $X$ 의 분산을 구하시오 (정수값으로 입력).
각 확률변수에서 기댓값을 뺀 값들을 각각 제곱하고, 모두 각각의 확률변수와 곱하여 더하면 되는 문제였습니다.
또는, 확률변수를 제곱한 값들의 기댓값을에서 기댓값 자체를 제곱한 값을 빼줘도 분산을 구할 수 있습니다.
References
- pandas - 최성철 교수님
- Mathematics for Artificial Intelligence - Unist 임성철 교수님

Leave a comment