그래프(Graph)

Graph

정점들과 간선들로 이루어진 집합이다.

V: Vertex, E: Edge, G: Graph
그래프 G는 (V, E)의 집합으로 정의 될 수 있다. => G = (V, E)
V(G)는 정점의 집합 그리고 E(G)는 두 정점들의 연결을 나타내는 간선의 집합이다.

Info: 그래프는 트리를 포함하는 개념이고, 트리는 사이클을 포함하지 않는 그래프라고 볼 수 있다.
그래서 모든 트리는 그래프이지만, 모든 그래프는 트리가 아니다.

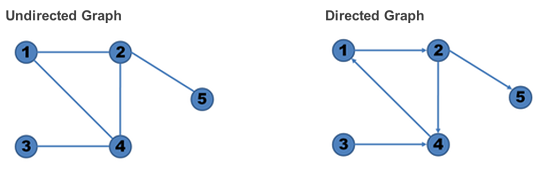
Undirected and Directed Graph

그래프는 방향 그래프 또는 비방향 그래프가 될 수 있다.

비방향 그래프는 두 정점 간의 간선에 방향이 없다.
A - B의 비방향 간선이 있다면, 이것은 A -> B로, B -> A로의 탐색이 가능하다는 것을 의미한다.

방향 그래프는 두 정점 간의 간선에 방향을 가지고 있다.
A -> B의 방향 간선이 있다면, 이것은 A -> B로의 탐색이 가능, 그러나 B -> A로의 탐색이 가능하지 않다는 것을 의미

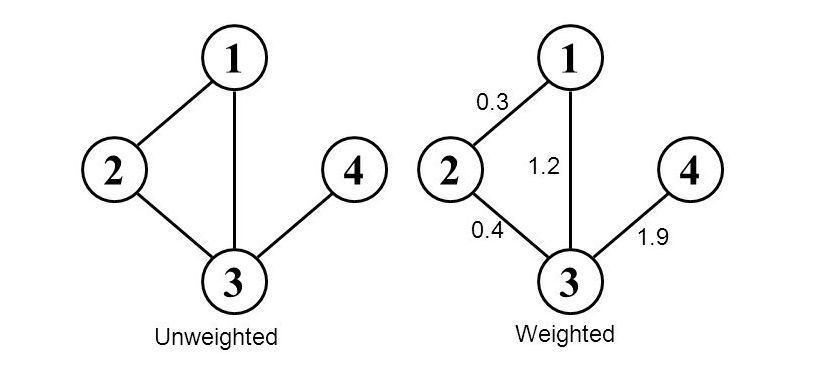
Unweighted and weighted Graph

두 정점 간의 간선에 추가 정보가 없다면 Unweighted(비가중치) 그래프.
두 정점 간의 간선에 추가 정보가 있다면 weighted(가중치) 그래프.

Representation

그래프를 표현하는 2가지 방법을 알아본다.

인접 행렬(Adjacency matrix)

2차원 행렬로 표현하는 방법.
행은 출발 정점을 나타내고 열을 도착 정점을 나타낸다. 꼭짓점 x에서 꼭짓점 y로 변이 존재하면 행렬 성분 x행 y열의 값은 1이고 그렇지 않으면 0이다.

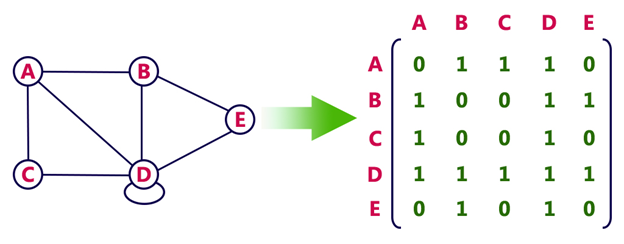
Note: 그래프가 100개의 정점과 1개의 간선으로 이루어져 있어도, 인접행렬 표현 시 100x100 크기의 매트릭스를 써야한다. 즉, 비교적 적은 간선의 그래프를 표현하는데에는 불필요한 공간이 많이 소비된다.

인접 리스트(Adjacency list)

인접 리스트를 이용하여 그래프를 표현하는 방법
이 표현에서는, 각 정점이 인접리스트 배열로 표현이 되어 있고, 자신과 인접한 노드들을 리스트로 연결한다.

표현방식: A - B 와 같이 방향성이 없을 때는 A의 인접리스트에 B 원소를 추가하고, B의 뒤에도 A를 추가한다.
A -> B 와 같이 방향성이 있을 때는 A의 인접리스트에 B 원소만 추가한다.

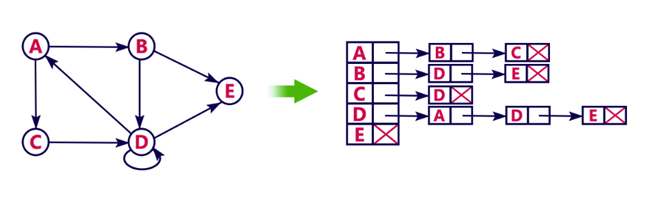
Note: 위 그래프는 방향 그래프임에 주의하라.
A 정점은 B와 C 노드와 이웃하므로 A의 인접리스트 뒤로 B와 C의 원소가 따라 붙는다.
B 정점은 D와 E 노드와 이웃하므로 B의 인접리스트 뒤로 D와 E의 원소가 따라 붙는다.

Pros: 인접 행렬 방식에 비해 메모리 공간을 많이 절약할 수 있다.
각 정점들 간의 이웃관계를 보다 쉽고 확실하게 표현할 수 있다.

Cons: 두 정점이 서로 연결되어 있는지 찾는 연산은 인접 행렬에 비해 다소 느리다.

Implementation

Example Graph

예제에서 나타내고자 하는 그래프는 다음과 같다.

Graph G (Bidirectional): 
V = (0, 1, 2, 3, 4)
E = (0, 1), (0, 2), (1, 2), (1, 3), (2, 4), (3, 4)

G:
0 ------ 2
|      /   \
|    /      4
|  /       /
1 ------ 3 

위 그래프로 부터 표현되어지는 인접 리스트는 다음과 같다.

0 => 1 => 2       // 0번 정점은 1, 2번 정점과 연결되어 있다.
1 => 0 => 2 => 3  // 1번 정점은 0, 2, 3번 정점과 연결되어 있다.
2 => 0 => 1 => 4  // 2번 정점은 0, 1, 4번 정점과 연결되어 있다.
3 => 1 => 4       // 3번 정점은 1, 4번 정점과 연결되어 있다.
4 => 2 => 3

Graph Class

public class Graph {
    private int V; // 그래프의 정점 갯수
    private LinkedList<Integer> adjListArray[]; // 그래프의 정점을 저장할 인접리스트 배열

    public Graph(int V) { // 그래프 생성자, 정점과 인접리스트 배열을 초기화 한다.
        this.V = V;
        adjListArray = new LinkedList[V]; // 인접리스트 배열 생성
        for (int i = 0; i < V; i++) {
            adjListArray[i] = new LinkedList<>(); // 인접리스트 노드 초기화 및 생성
        }
    }
}

addEdge

// 양방향 간선 정보 저장
static void addEdge(Graph graph, int src, int dest) { 
    graph.adjListArray[src].add(dest); // src -> dest
    graph.adjListArray[dest].add(src); // dest -> src
}

---

Graph.java

import java.util.LinkedList;

public class Graph {
    private int V; // 그래프의 정점 갯수
    LinkedList<Integer> adjListArray[]; // 그래프의 정점을 저장할 인접리스트 배열

    public Graph(int V) { // 그래프 생성자, 정점과 인접리스트 배열을 초기화 한다.
        this.V = V;
        adjListArray = new LinkedList[V];
        for (int i = 0; i < V; i++) {
            adjListArray[i] = new LinkedList<>();
        }
    }
    // 그래프 출력 메소드
    public void printGraph() {
        for (int v = 0; v < V; v++) {
            System.out.print(v);
            for (Integer i : adjListArray[v]) {
                System.out.print(" => " + i);
            }
            System.out.print("\n");
        }
    }
    // 양방향 간선 생성 메소드
    static void addEdge(Graph graph, int src, int dest) {
        graph.adjListArray[src].add(dest);
        graph.adjListArray[dest].add(src);
    }


    public static void main(String[] args) {
        int V = 5; // 정점의 갯수는 5개 (0, 1, 2, 3, 4)
        Graph graph = new Graph(V); // 그래프 초기화

        addEdge(graph, 0, 1); // 0번과 1번을 정점으로 하는 간선을 생성한다.
        addEdge(graph, 0, 2); // 0번과 2번을 정점으로 하는 간선을 생성한다.
        addEdge(graph, 1, 2); // 1번과 2번을 정점으로 하는 간선을 생성한다.
        addEdge(graph, 1, 3);
        addEdge(graph, 2, 4);
        addEdge(graph, 3, 4);

        graph.printGraph();
    }
}

Output:
0 => 1 => 2       // 0번 정점은 1, 2번 정점과 연결되어 있다.
1 => 0 => 2 => 3  // 1번 정점은 0, 2, 3번 정점과 연결되어 있다.
2 => 0 => 1 => 4  // 2번 정점은 0, 1, 4번 정점과 연결되어 있다.
3 => 1 => 4       // 3번 정점은 1, 4번 정점과 연결되어 있다.
4 => 2 => 3       // 4번 정점은 2, 3번 정점과 연결되어 있다.

References

Graph - Wikipedia
Graph - javapoint