위상정렬(Topological sorting)
컴퓨터 과학에서 위상정렬(Topological sorting)은 방향 그래프에서 정점들의 선형적인 순서를 말하는데, 여기서 정점들의 선형적 순서란 정점 u로 부터 정점 v로 가는 간선에 대해 순서상 정점 u가 정점 v보다 앞에 있다는 것을 뜻한다. 예를 들어, 방향 그래프에서 정점들은 수행될 작업들을 뜻할 수 있고, 간선은 어떤 작업이 다른 작업보다 먼저 수행되어야 한다는 제약을 나타낼 수 있다. 즉, 위상정렬의 결과는 작업들이 수행되는 일련의 순서를 의미한다. 위상정렬은 사이클이 형성되지 않은 그래프에서 가능하다. 즉, 사이클이 없는 방향 그래프에서 적용이 가능한데, 이런 그래프를 DAG(Directed acyclic graph)라고 한다. 어떤 DAG에 대해서도 위상정렬을 적용하면 적어도 하나의 위상순서를 가지게 되고 경우에 따라 여러개의 위상순서를 가질수 있다. 위상정렬 알고리즘은 DAG에서 위상순서를 구하는데 선형시간이 걸린다고 알려져 있다.
Example
위상정렬은 현실적인 예로는 제약에 따른 작업들의 스케줄링 순서라고 이해하면 된다. 작업들은 정점으로 나타내어지고 정점에서 다른 정점으로의 간선이 있는데, 이는, x, y 두 정점을 끝 점으로 하고 x->y로의 방향 간선 E(x,y)이 있을 때 작업 y가 수행되기 위해서는 x가 사전에 먼저 수행 완료되어야 한다는 것을 뜻한다. 작업 y의 제약은 x인 것이다. 이처럼 제약이 있는 해당 작업들에 대해서 위상정렬은 작업들의 수행순서를 나타낸다.
밑 그림에서 5번 정점과 11번 정점을 보자. 정점은 작업으로 생각하고 간선은 제약 또는 작업 흐름으로 보면 위상정렬에서는 5번 작업이 완료되고 11번 작업이 수행된다는 것이다. 즉, 11번 작업이 수행되기 위해선 5번 작업이 사전에 완료가 되어야 한다는 것을 말한다. 다른 작업들도 마찬가지로, 9번 정점이 수행되기 위해서는 11번과 8번 작업이 사전에 완료가 되어야 한다.
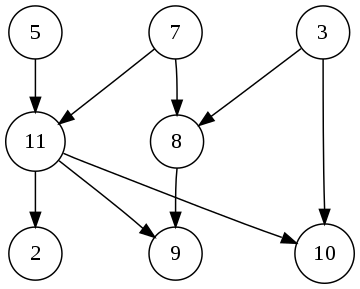
위상순서: DAG의 모든 간선 u->v에 대해서, 정점 u는 v보다 순서상에서 먼저 나와야 한다.
다음은 위 그림에서의 위상정렬 순서인데 기준에 따라 여러가지가 있을 수 있다.
5->7->3->11->8->2->9->10(왼쪽에서 오른쪽, 밑에서 아래로)3->5->7->8->11->2->9->10(현재 작업 가능한 작업들의 번호가 작은순서)3->7->8->5->11->10->2->9(현재 작업 가능한 작업들의 무작위 선택)
Algorithm
DAG에서의 위상정렬을 구하는 두 가지 알고리즘을 살펴보자.
이 두 알고리즘은 모두 $O(V+E)$의 선형시간에 동작한다. V는 정점의 개수, E는 간선의 개수이다.
Kahn’s algorithm
위상정렬을 구하는 이 알고리즘은 Kahn (1962)에 의해 처음 소개 되었다.
Kahn’s algorithm은 해당 그래프에서의 진입간선(Incoming edge)을 가지고 있지 않은 정점으로 부터 시작해서 그 정점과 연결된 정점의 진입간선(Incoming edge)을 삭제 하면서 동작한다.
다음은 Kahn’s algorithm의 위상정렬 의사코드이다.
S ← Set of all nodes with no incoming edge
L ← Empty list that will contain the sorted elements
while S is non-empty do
remove a node n from S
add n to tail of L
for each node m with an edge e from n to m do
remove edge e from the graph
if m has no other incoming edges then
insert m into S
if graph has edges then
return error (graph has at least one cycle)
else
return L (a topologically sorted order)
- 진입간선이 없는 없는 정점들을 시작 리스트 S에 넣는다.
- S가 빈 공간이 아닐 때 까지 다음을 반복한다.
- S의 앞에서 부터 정점 n을 하나 취해서 위상정렬 리스트 L의 끝에 추가한다.
- 정점 n과 m을 양 끝점으로 하는 간선 e와 정점 m에 대해서
- 간선 e를 삭제한다. (정점 m의 진입간선 삭제와 같은 의미이다.)
- 정점 m의 진입간선의 개수가 0개라면, S에 m을 추가한다.
- 그래프에 간선이 남아있으면 적어도 하나의 사이클이 있다는 의미이므로 error를 리턴한다. 그렇지 않으면 위상정렬 순서를 리턴한다.
위상정렬을 적용할 그래프가 DAG이라면 이 알고리즘은 위상정렬 순서 L을 리턴할 것이고, 그래프에 사이클이 하나라도 있다면 위상정렬은 불가능하다.
집합 S에서 n이 삭제되는 순서에 따라 위상정렬의 결과는 달라지기 때문에, 한 그래프에서 위상정렬은 특정하지 않고 여러개가 존재할 수 있다. S는 큐와 스택 같은 정점들을 담을 수 있는 집합이 될 수 있다.
구현에 있어서 간선을 삭제하는 방법과 정점 m의 진입간선 개수를 추적하는 방법은 각 정점마다 진입간선의 개수를 가지고 있는 배열을 둠으로써 쉽게 구현이 가능하다.
- indegree[m]은 m의 진입간선 개수를 의미한다.
- indegree[m] = indegree[m] - 1 을 함으로써 m의 진입간선을 하나 삭제할 수 있다.
- indegree[m] == 0 이면 m의 진입간선은 없으므로 m을 S에 추가한다.
Depth-first search
위상정렬을 구하는 다른 방법은 깊이우선탐색(Depth-first search)에 기반한 것이다.
이 방법은 그래프의 기준에 따라 또는 임의의 순서로 노드들을 탐색해 나가다가 이미 방문이 완료된 정점 또는 더 이상 탐색할 정점을 가지지 않은 정점에 대해서 위상정렬 리스트에 노드를 추가하는 방법이다.
다음은 Depth-first search에 기반한 위상정렬의 의사코드이다.
permanent mark: 더 이상 방문할 정점이 없어 DFS 탐색이 끝난 정점의 표시를 뜻한다.temporary mark: DFS 탐색이 진행 중인 정점의 표시를 뜻한다.
L ← Empty list that will contain the sorted nodes
while exists nodes without a permanent mark do
select an unmarked node n
visit(n)
function visit(node n)
if n has a permanent mark then
return
if n has a temporary mark then
stop (not a DAG)
mark n with a temporary mark
for each node m with an edge from n to m do
visit(m)
remove temporary mark from n
mark n with a permanent mark
add n to head of L
DAG에서 방문완료 되지 않은 정점들이 있는 동안, 정점을 하나 선택해 탐색을 진행한다.
function visit(node n):
- 정점 n이 방문완료 정점이면 백트랙 한다.
- 정점 n이 현재 방문 중인 정점이면 역 간선(Back edge)이 있다는 것이므로 사이클이 있다는 말이된다. 알고리즘을 종료한다.
- 위 1, 2번 조건이 아니라면, 정점 n을 진행 중인 정점으로 표시한다.
- 정점 n과 m을 양 끝점으로 하는 간선의 정점 m에 대해서
정점 m을 재귀적으로 탐색한다. (1번으로 간다.) - 정점 n을 방문완료 표시하고 L의 맨 처음에 추가한다.
DFS 함수에서 temporary mark검사를 하고 있는데, DFS 탐색에 있어서 방문되어 지고 있는 정점이 방문완료 되지 못한 채 다른 정점에 의해서 방문이 되면, 역 간선(Back edge)이 있다는 의미가 된다. 이는 사이클이 있다는 것과 같은 의미이다.
Implementation
다음의 구현들은 밑의 그래프를 예제로 사용하였다.
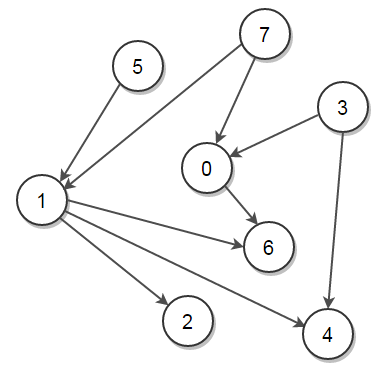
다음은 Kahn’s algorithm을 구현한 java 코드이다.
- Graph class: 간선 정보들로 부터 그래프를 구축한다.
indegree.set(dest, indegree.get(dest) + 1);: 간선 정보들로 부터 그래프를 구축하면서 해당 정점에 해당하는 진입간선을 하나씩 추가한다.Stack<Integer> S = new Stack<>();: 정점들을 담을 집합 S로는 스택을 사용하였다.
import java.util.*;
// data structure to store graph edges
class Edge
{
int source, dest;
public Edge(int source, int dest) {
this.source = source;
this.dest = dest;
}
};
// class to represent a graph object
class Graph
{
// A List of Lists to represent an adjacency list
List<List<Integer>> adjList = null;
// stores indegree of a vertex
List<Integer> indegree = null;
// Constructor
Graph(List<Edge> edges, int N) {
adjList = new ArrayList<>(N);
for (int i = 0; i < N; i++) {
adjList.add(i, new ArrayList<>());
}
// initialize indegree of each vertex by 0
indegree = new ArrayList<>(Collections.nCopies(N, 0));
// add edges to the undirected graph
for (int i = 0; i < edges.size(); i++)
{
int src = edges.get(i).source;
int dest = edges.get(i).dest;
// add an edge from source to destination
adjList.get(src).add(dest);
// increment in-degree of destination vertex by 1
indegree.set(dest, indegree.get(dest) + 1);
}
}
}
class TopologicalSort
{
// performs Topological Sort on a given DAG
public static List<Integer> doTopologicalSort(Graph graph, int N)
{
// list to store the sorted elements
List<Integer> L = new ArrayList<>();
// get indegree information of the graph
List<Integer> indegree = graph.indegree;
// Set of all nodes with no incoming edges
Stack<Integer> S = new Stack<>();
for (int i = 0; i < N; i++) {
if (indegree.get(i) == 0) {
S.add(i);
}
}
while (!S.isEmpty())
{
// remove a node n from S
int n = S.pop();
// add n to tail of L
L.add(n);
for (int m : graph.adjList.get(n))
{
// remove edge from n to m from the graph
indegree.set(m, indegree.get(m) - 1);
// if m has no other incoming edges then
// insert m into S
if (indegree.get(m) == 0) {
S.add(m);
}
}
}
// if graph has edges then graph has at least one cycle
for (int i = 0; i < N; i++) {
if (indegree.get(i) != 0) {
return null;
}
}
return L;
}
public static void main(String[] args)
{
// List of graph edges as per above diagram
List<Edge> edges = Arrays.asList(
new Edge(0, 6), new Edge(1, 2), new Edge(1, 4),
new Edge(1, 6), new Edge(3, 0), new Edge(3, 4),
new Edge(5, 1), new Edge(7, 0), new Edge(7, 1)
);
// Set number of vertices in the graph
final int N = 8;
// create a graph from edges
Graph graph = new Graph(edges, N);
// Perform Topological Sort
List<Integer> L = doTopologicalSort(graph, N);
if (L != null) {
System.out.print(L); // print topological order
} else {
System.out.println("Graph has at least one cycle. " +
"Topological sorting is not possible");
}
}
}
Output:
7 5 1 2 3 4 0 6

Leave a comment