Quick sort
퀵 소트(Quick sort)는 효율적인 비교기반 정렬 알고리즘으로 영국의 컴퓨터 과학자 Tony Hoare에 의해 1959 년에 개발되었다. 이 정렬 알고리즘은 현재 여러 프로그래밍 언어의 공식 정렬 라이브러리로 채택이 되었고, 실무에서도 많이 쓰이고 있다. 구현이 잘 되었을 때는 시간복잡도 $O(nlogn)$의 머지 소트나 힙 소트보다 두 배에서 세 배 정도 빨라질 수 있다.
퀵 소트는 분할 정복 알고리즘이다. 배열에서 원소를 두 부분의 서브 배열(sub-array)로 나눌 기준이 되는 피봇(pivot)을 선택하고 피봇 값 보다 크고 작음에 따라 원소를 두 부분의 서브 배열로 나눈다. 피봇을 기준으로 두 서브 배열이 부분 정렬이 되면, 서브 배열은 다시 재귀적(recursively)으로 위와 같이 정렬이 되어진다.
퀵 소트에서 원소가 피봇을 기준으로 두 부분의 서브 배열로 분할 되는 것은 약간의 변수와 같은 상수적 메모리 공간 $O(1)$만을 요구하는 제자리 정렬(in-place)의 속성을 만족 할 수 있다.
퀵 소트는 비교기반 정렬 알고리즘으로서 원소들이 크고 작음의 관계에 따라 상대적인 위치가 정해지게 된다. 대소 관계를 정의할 수 있는 형태는 이 비교기반에 따라 정렬이 가능해진다. 또한 현재 퀵 소트의 효율적인 알고리즘은 안정 정렬(Stable sort)이 아니다. 이 것은 같은 값을 가진 원소의 상대적인 위치가 정렬이 되고 난 후에는 변할 수도 있다는 것을 의미한다.
퀵 소트의 시간복잡도 분석에 따르면 평균적인 상황에서는(서브 배열의 크기를 25% or 75%로 나눌 수 있는 피봇을 원소로 선정) $n$개의 원소를 정렬할 때 성능이 $O(nlogn)$, 최악의 상황에서는(서브 배열이 매 단계마다 1크기 만큼 줄어드는 상황) 성능이 $O(n^2)$임을 보인다. 최악의 경우는 대부분 많이 드물며 세부 구현에 따라 복잡도가 다소 달라질 수 있다.
안정 정렬과 제자리 정렬 이란?
안정 정렬: 정렬이 끝나면 같은 키값을 가진 원소들의 상대적인 순서가 변하지 않는 것을 의미.
안정 정렬 알고리즘으로는 삽입 정렬, 머지 소트, 카운팅 소트 등이 있다.
제자리 정렬: 원소들의 개수에 비해서 충분히 무시할 만한 저장 공간만을 더 사용하는 정렬 알고리즘들을 의미.
예를 들어 삽입 정렬은 이미 주어진 원소들을 옮긴 뒤 적절한 위치에 원소를 삽입하는 연산을 반복하는데, 이 과정에서 원소들을 담는 공간 외에 추가로 사용될 수 있는 공간은 옮겨지는 원소가 저장되는 공간과 루프 변수 정도에 불과하다.
Algorithm
퀵 소트는 분할 정복 알고리즘으로 피봇 원소를 기준으로 입력 배열을 두개의 부분 배열로 나눈다.(하나는 피봇 보다 작거나 같은 원소들, 하나는 피봇보다 큰 원소들) 그리고 나뉜 두개의 부분 배열을 각각 재귀적으로 다시 분할 정복 정렬 한다.
다음은 퀵 소트의 알고리즘이다. (오름차순 기준)
-
배열에서 피봇(pivot)을 하나 선정한다.
-
피봇 값을 기준으로 배열의 원소들을 두 개의 부분 배열로 구분한다. 피봇보다 작은 원소는 피봇의 앞의 부분 배열에, 피봇보다 큰 원소는 피봇의 뒷 부분 배열에 놓는다. 구분이 완료되면 피봇을 배열의 최종적인 위치(원소들을 기준으로 절대적으로 위치해야만 하는 특정 위치)에 놓는다. 이 두 번째 스텝을 분할(Partition)이라고 한다.
-
피봇을 기준으로 나뉜 두 부분 배열에 대해 위의 1, 2번 연산들을 재귀적으로 적용한다.
Step by Step
실제 예를 들어 퀵 소트가 어떻게 동작 되는지 알아본다.
가정
- 원소를 오름차순으로 정렬한다.
- 피봇은 배열의 맨 마지막 원소로 선정한다. (피봇 선정 방법은 여러가지가 있다.)
- 배열의 크기가 1 이하에 대해서는 퀵 소트를 수행하지 않는다. (크기가 1인 배열은 이미 정렬이 되어있다.)
위 알고리즘의 2번째 스텝 분할(Partition)을 세분화하여 보면 다음과 같다.
-
배열의 맨 첫번째 원소를 가리키는(인덱스 0) Left 포인터를 둔다.
-
피봇 바로 앞의 원소를 가리키는(피봇 인덱스 -1) Right 포인터를 둔다.
-
Left 포인터가 Right 포인터보다 작거나 같을 동안 & Left 포인터가 가리키는 원소가 피봇이 가리키는 원소보다 크거나 같을 때 까지 Left 포인터 위치를 1씩 증가시킨다.
-
Left 포인터가 Right 포인터보다 작거나 같을 동안 & Right 포인터가 가리키는 원소가 피봇이 가리키는 원소보다 작을 때 까지 Right 포인터 위치를 1씩 감소시킨다.
-
Left > Right가 아니라면 Left와 Right 포인터가 가리키는 원소를 서로 스왑한다.
그리고 3번으로 간다. -
Left > Right이라면 Left가 가리키는 원소와 피봇이 가리키는 원소를 서로 스왑 함으로써 피봇이 가리키던 원소의 최종적인 위치가 정해진다.
다음은 예제에 사용될 배열이다.
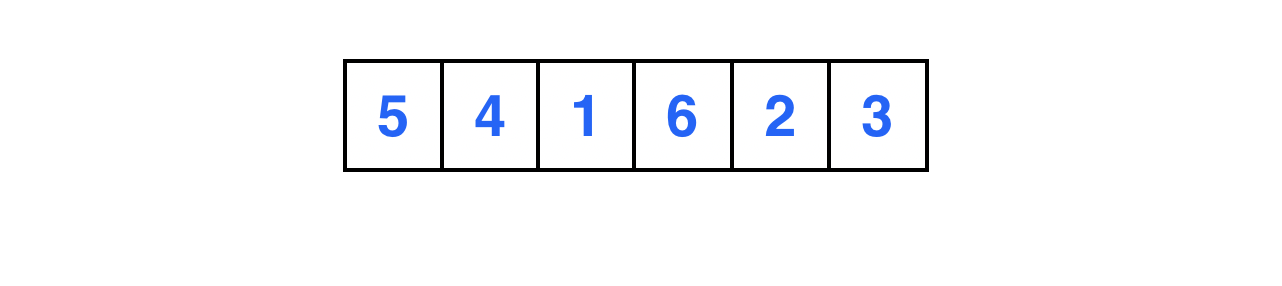
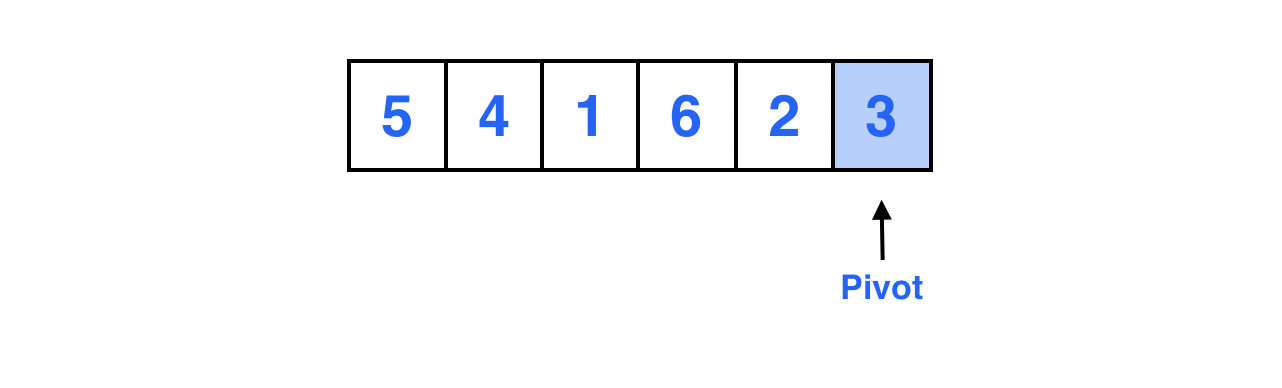
맨 마지막 원소를 피봇으로 선정한다.
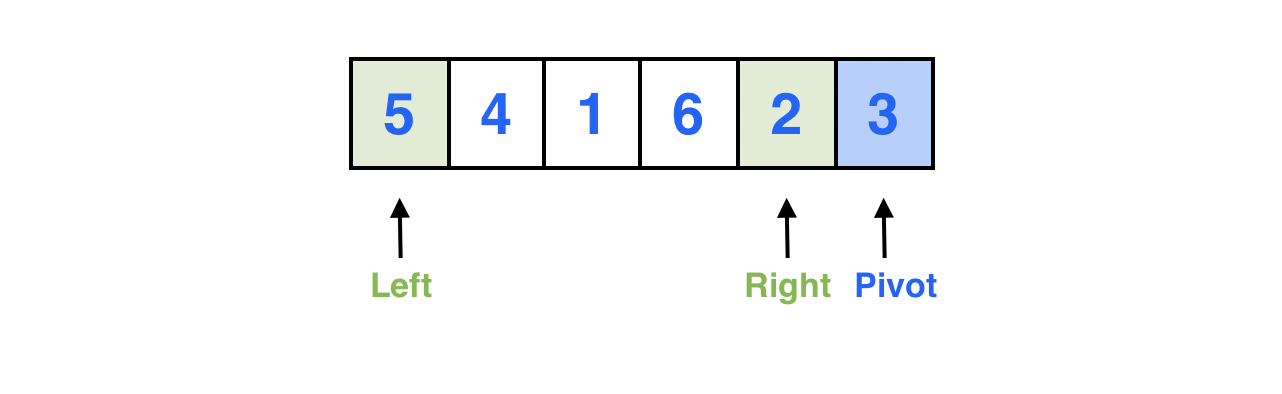
Left 포인터는 배열의 0 번째 인덱스를 가리키고, Right 포인터는 피봇 바로 앞의 원소를 가리킨다.
위 설명에 따라 포인터를 움직인다.
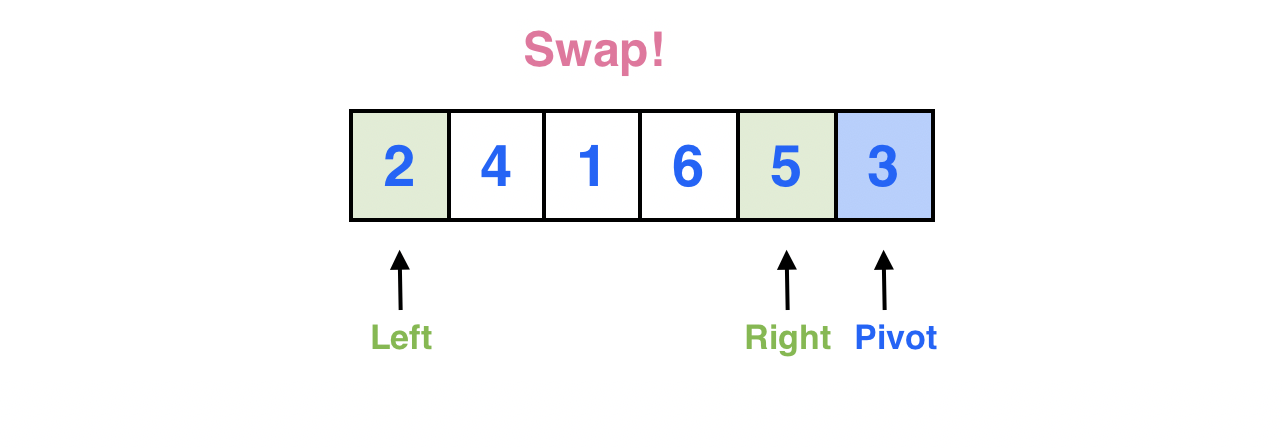
Left > Right가 아니므로 Left와 Right 포인터가 가리키는 원소를 서로 스왑한다.
알고리즘에 의해 Left와 Right 포인터를 움직인다.
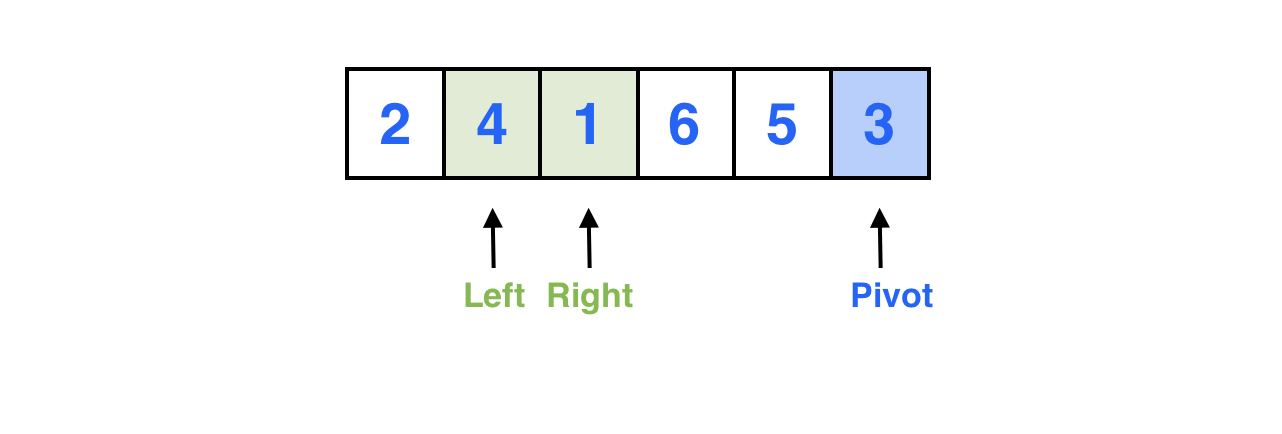
Left > Right가 아니므로 Left와 Right 포인터가 가리키는 원소를 서로 스왑한다.
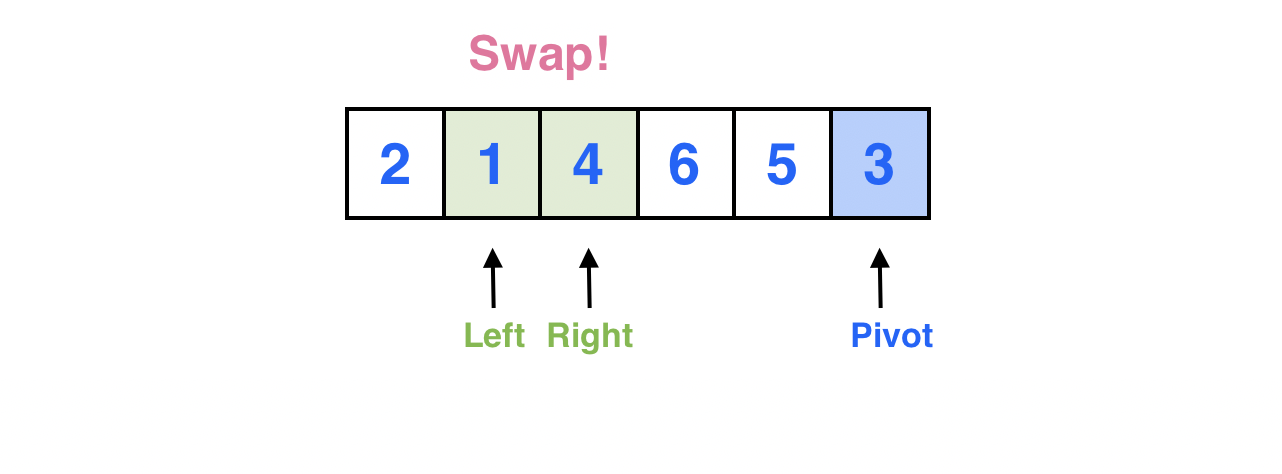
알고리즘에 의해 Left와 Right 포인터를 움직인다.
Left > Right가 되었다.
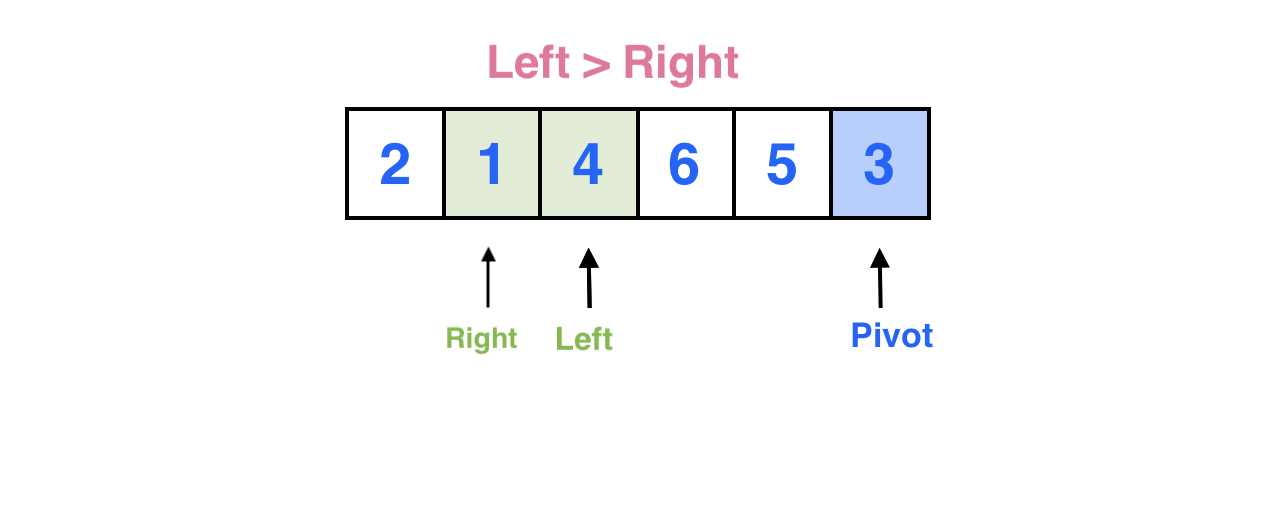
Left가 가리키는 원소와 피봇이 가리키는 원소를 서로 스왑한다.
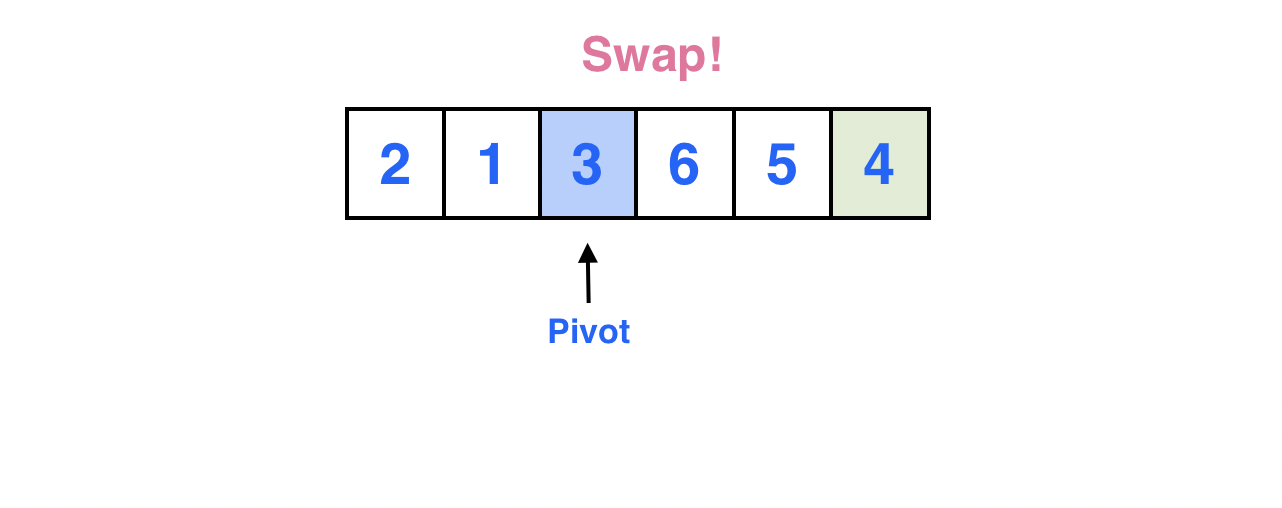
피봇이 가리키는 원소의 최종적인 위치가 정해진 모습이다.
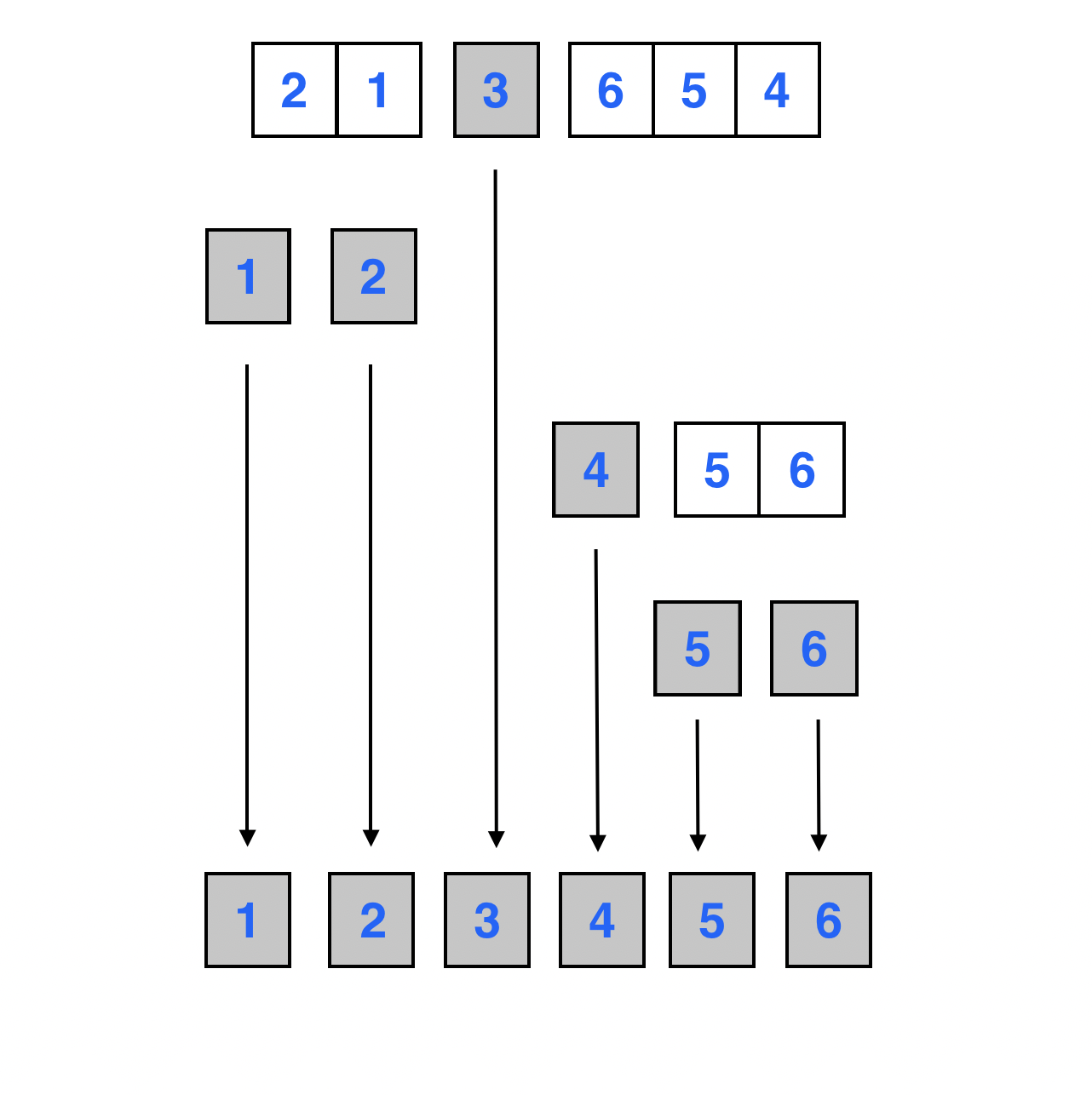
피봇을 기준으로 두개의 부분 배열로 분할이 되고, 왼쪽 부분 배열에는 피봇보다 작은 원소, 오른쪽 부분 배열에는 피봇보다 큰 원소들로 구성되었음을 볼 수 있다.
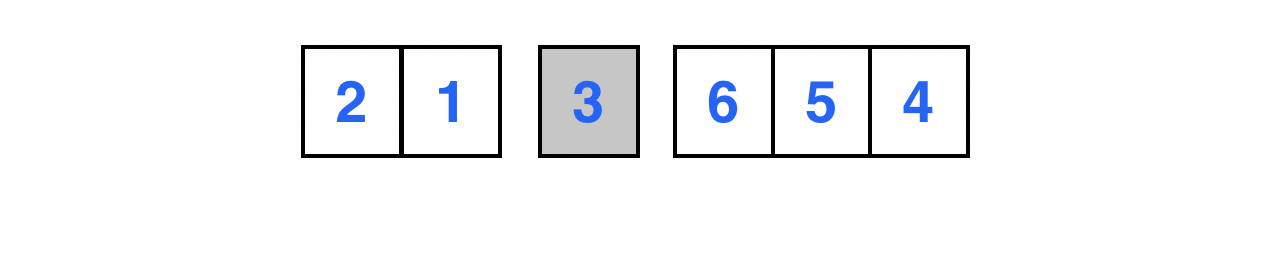
계속해서 왼쪽 부분 배열에 대해 재귀적으로 퀵 소트를 수행한다.
맨 마지막 원소를 피봇으로 선정한다.
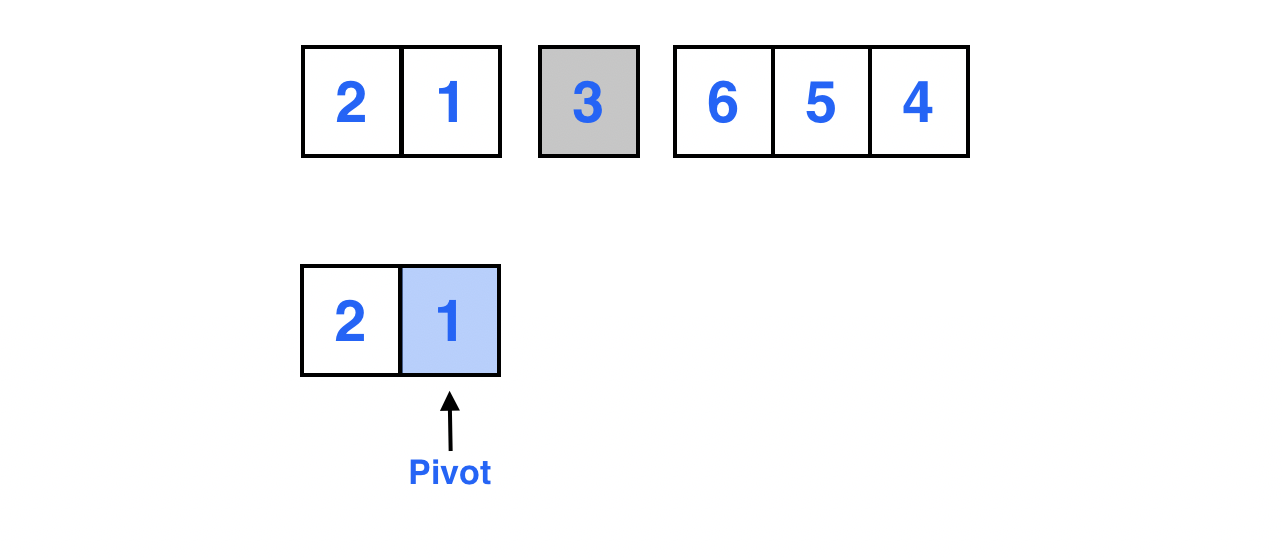
Left 포인터는 배열의 0 번째 인덱스를 가리키고, Right 포인터는 피봇 바로 앞의 원소를 가리킨다.
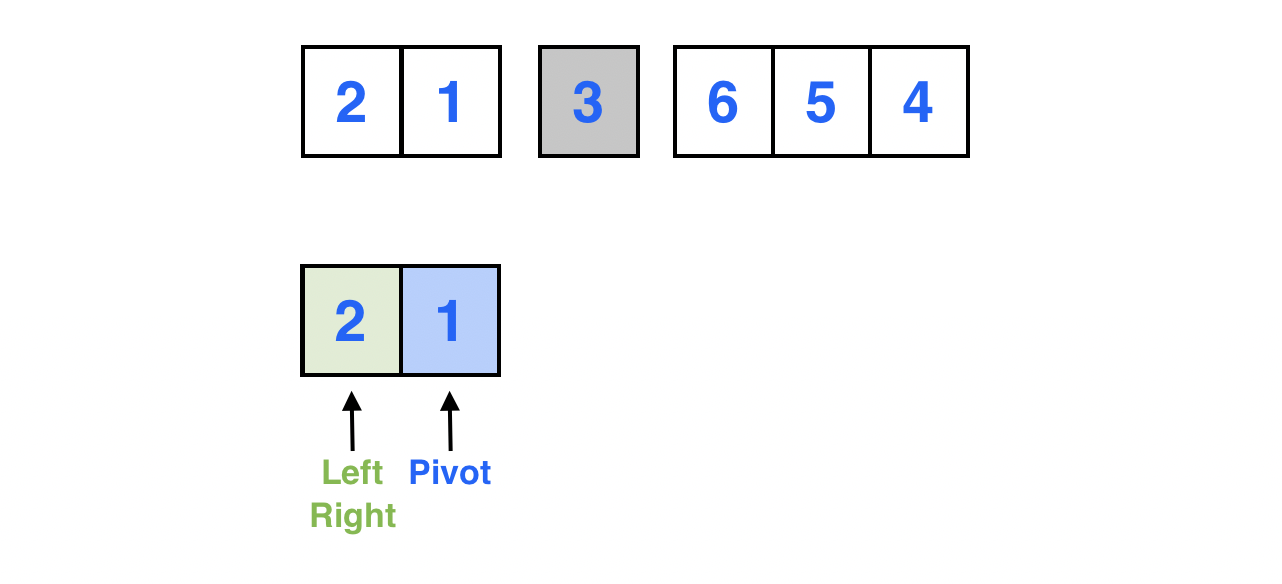
알고리즘에 의해 포인터를 움직인다.
Left > Right가 되었다.
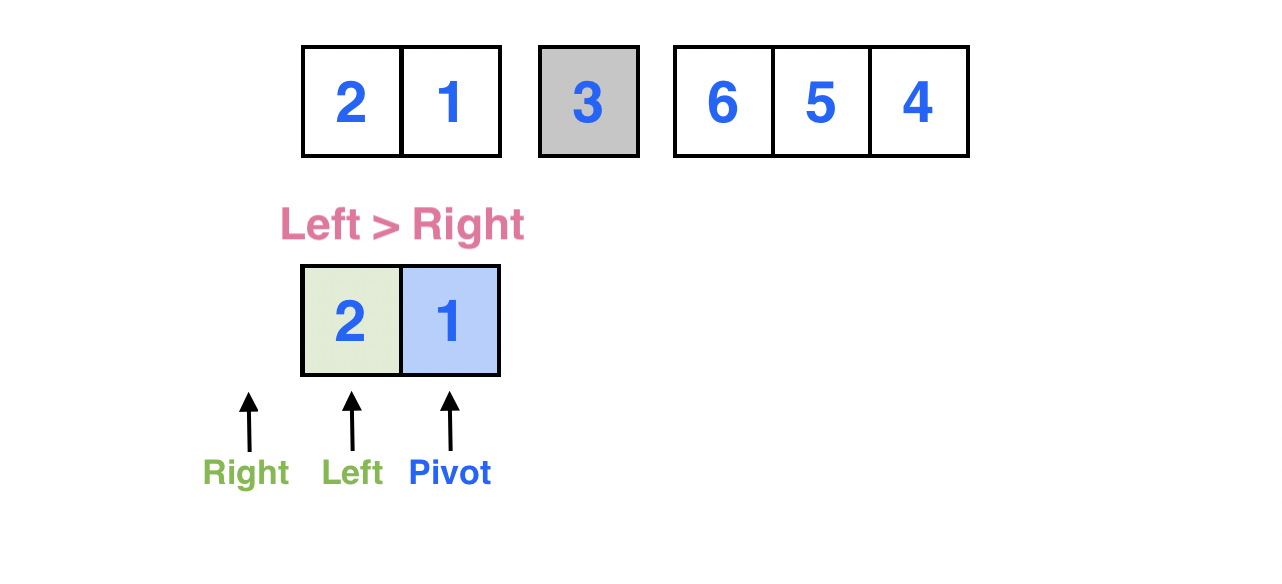
Left가 가리키는 원소와 피봇이 가리키는 원소를 서로 스왑한다.
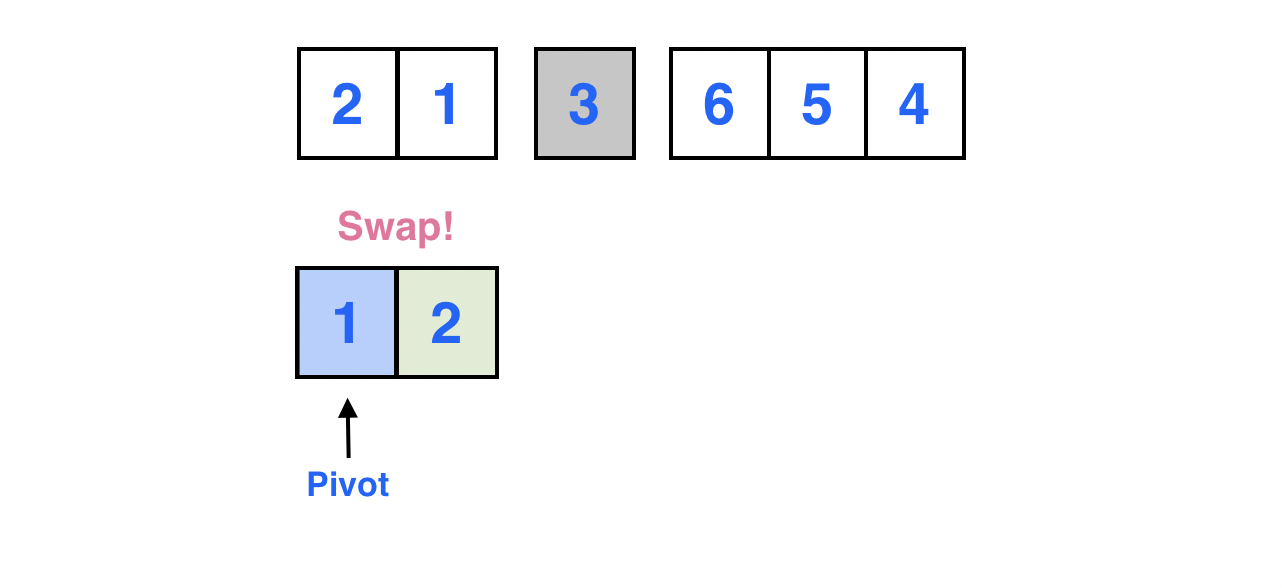
피봇이 가리키는 원소 1의 최종적인 위치가 정해진 모습이다.
원소 1을 기준으로 양 옆의 두 부분 배열은 모두 크기가 1 이하이므로 퀵소트를 수행하지 않는다.
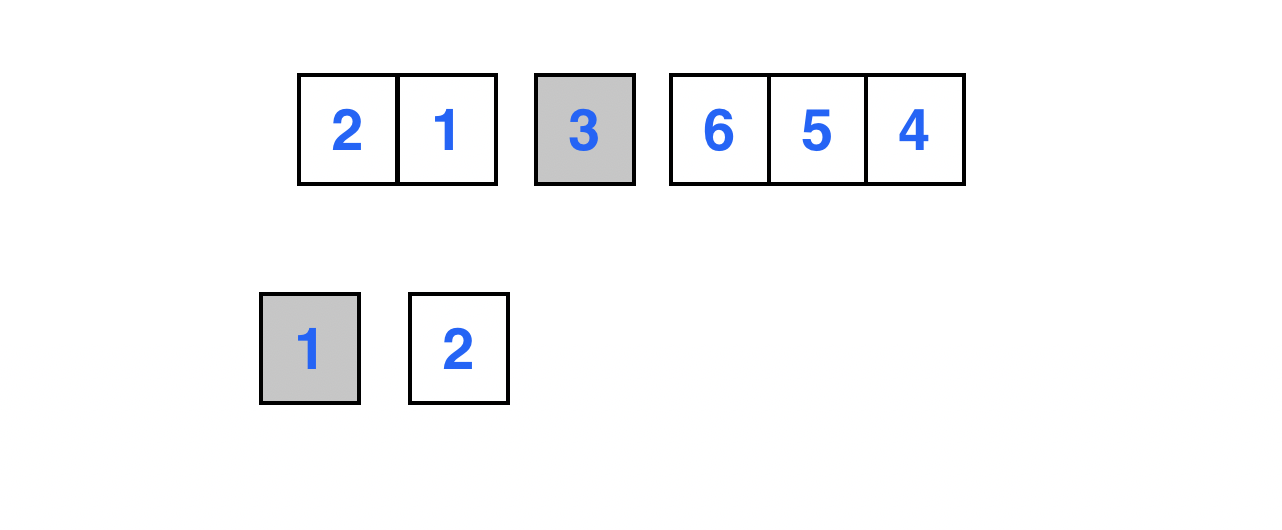
원소 2의 최종적인 위치가 정해진 모습이다.
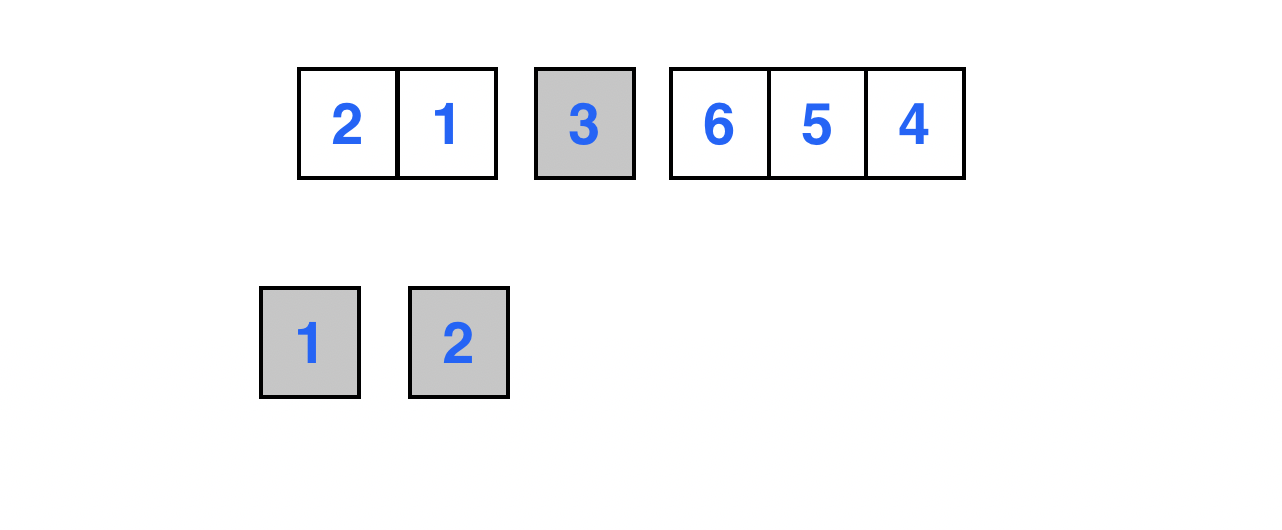
계속해서 3의 오른쪽 부분 배열 [6, 5, 4]가 재귀적으로 정렬이 된다.
맨 마지막 원소를 피봇으로 선정한다.
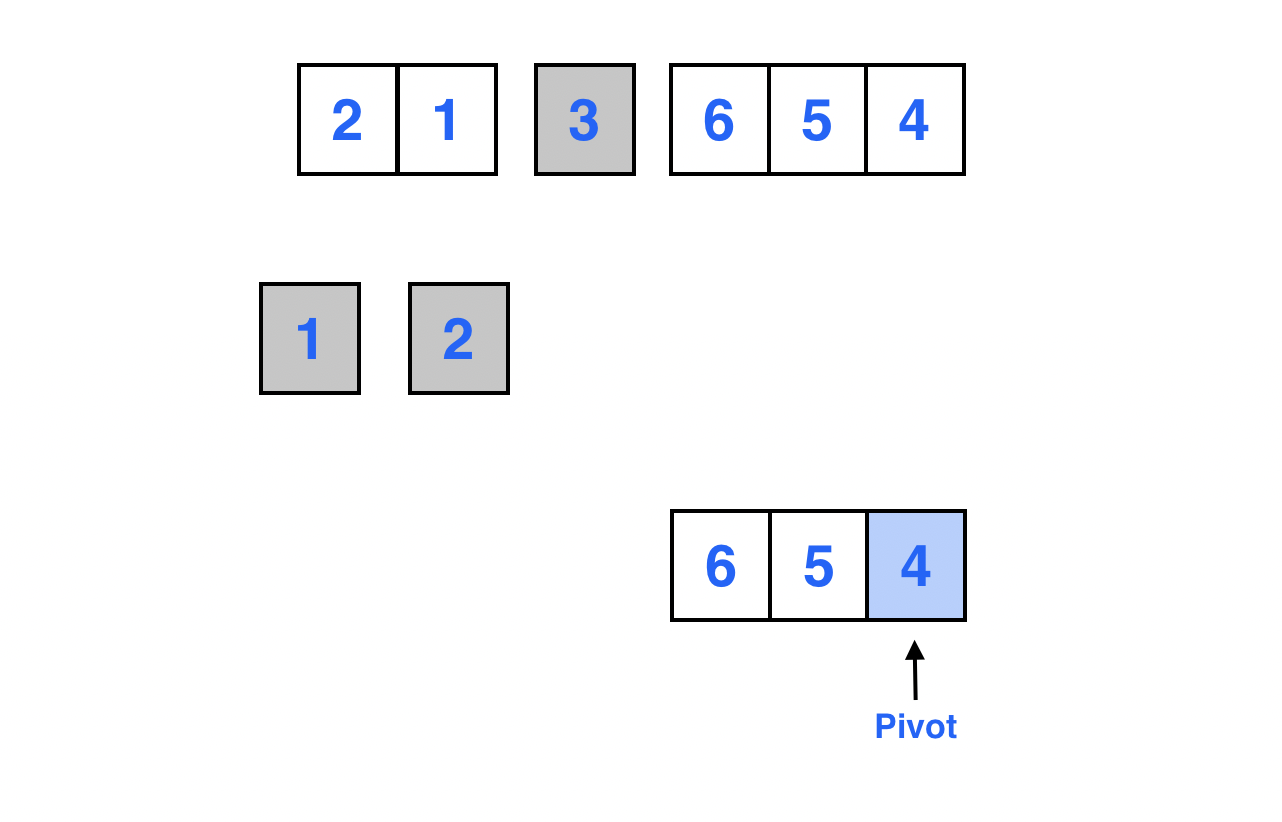
Left 포인터는 배열의 0 번째 인덱스를 가리키고, Right 포인터는 피봇 바로 앞의 원소를 가리킨다.
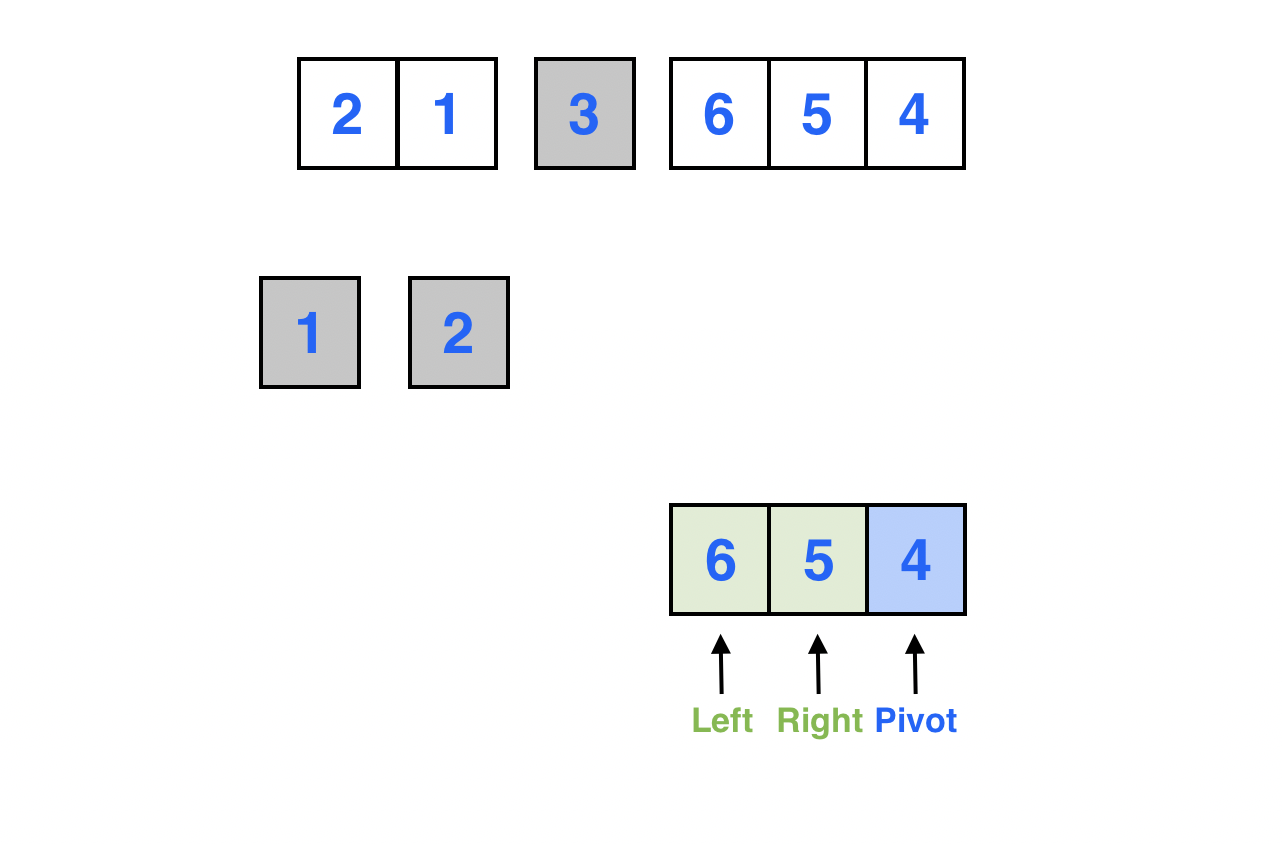
알고리즘에 의해 포인터를 움직인다.
Left > Right가 되었다.
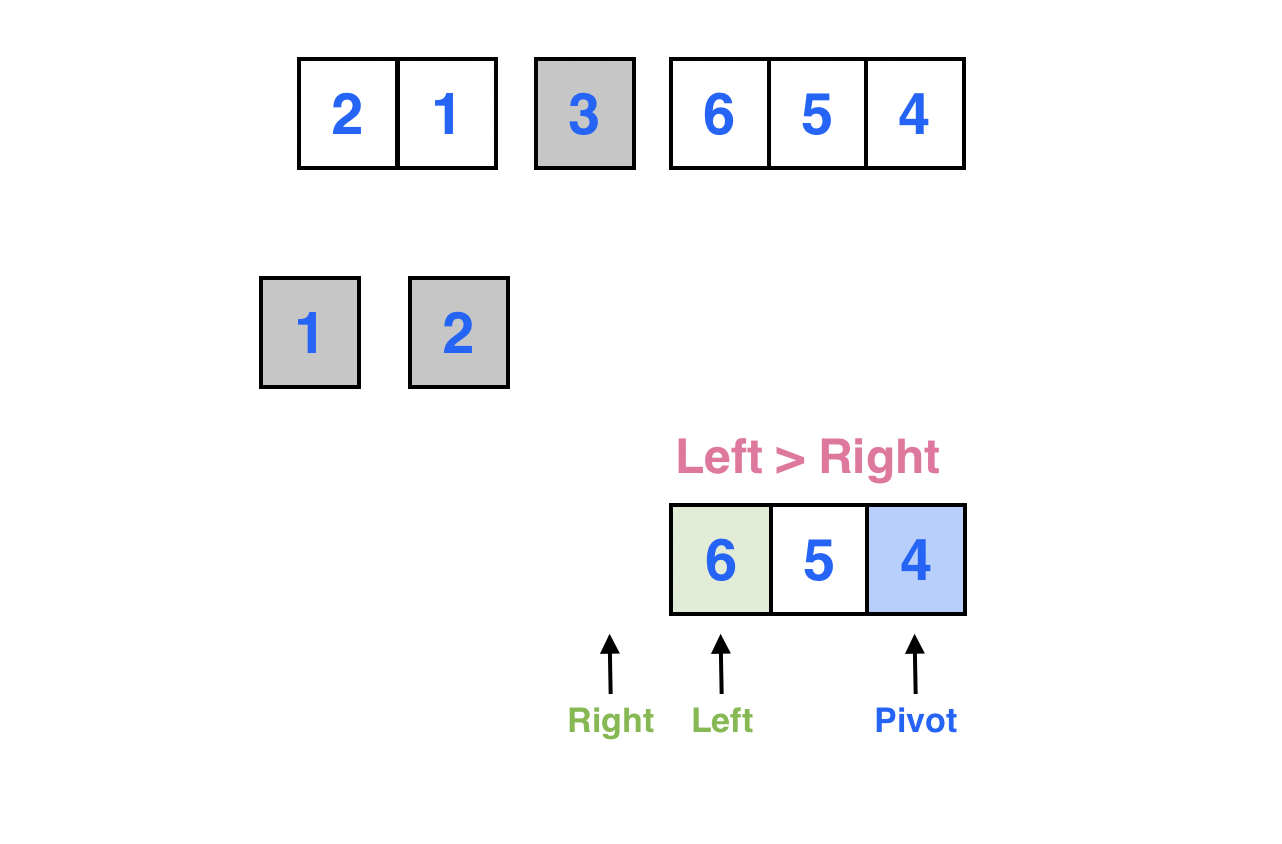
Left가 가리키는 원소와 피봇이 가리키는 원소를 서로 스왑한다.
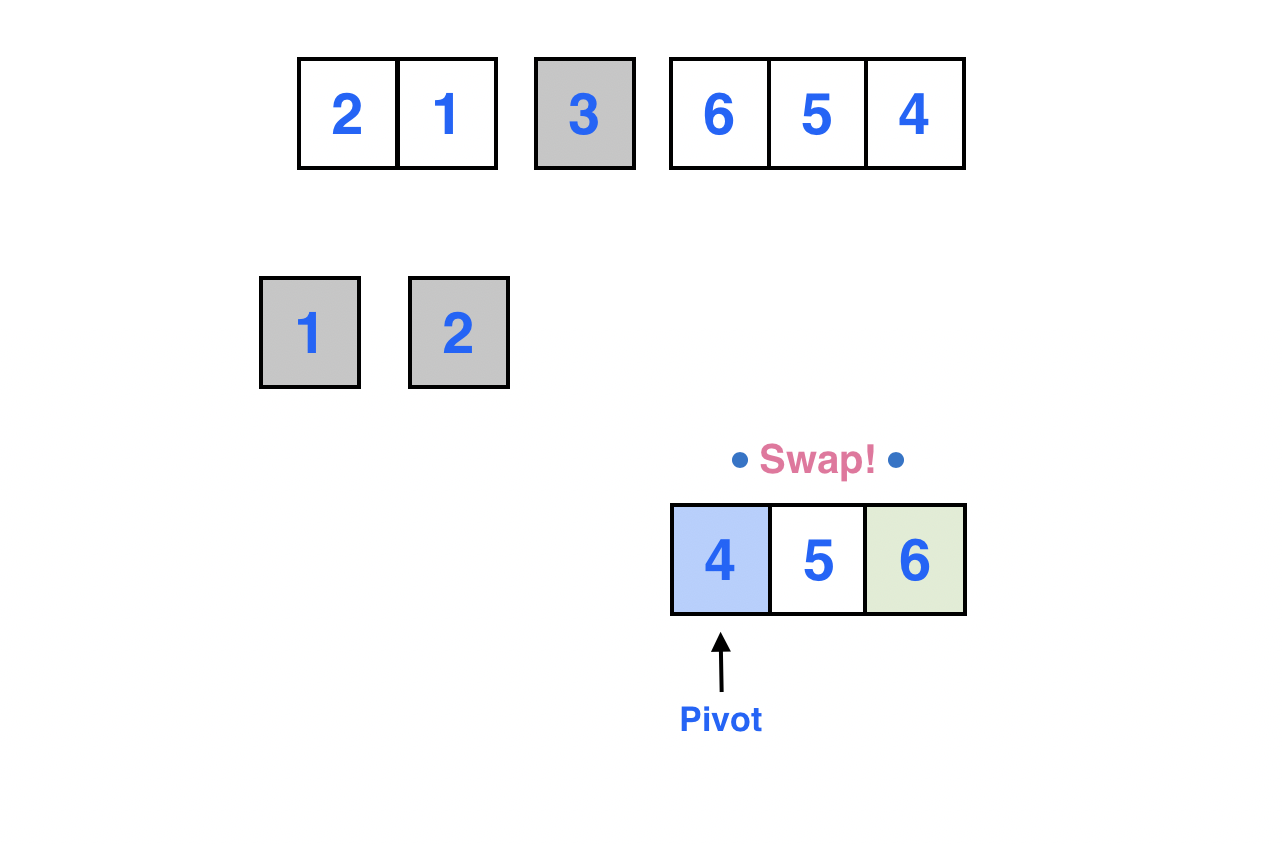
피봇이 가리키는 원소 4의 최종적인 위치가 정해진 모습이다.
원소 4의 왼쪽 부분 배열은 크기가 1 이하이므로, 오른쪽 배열에 대해 재귀적으로 정렬을 수행한다.
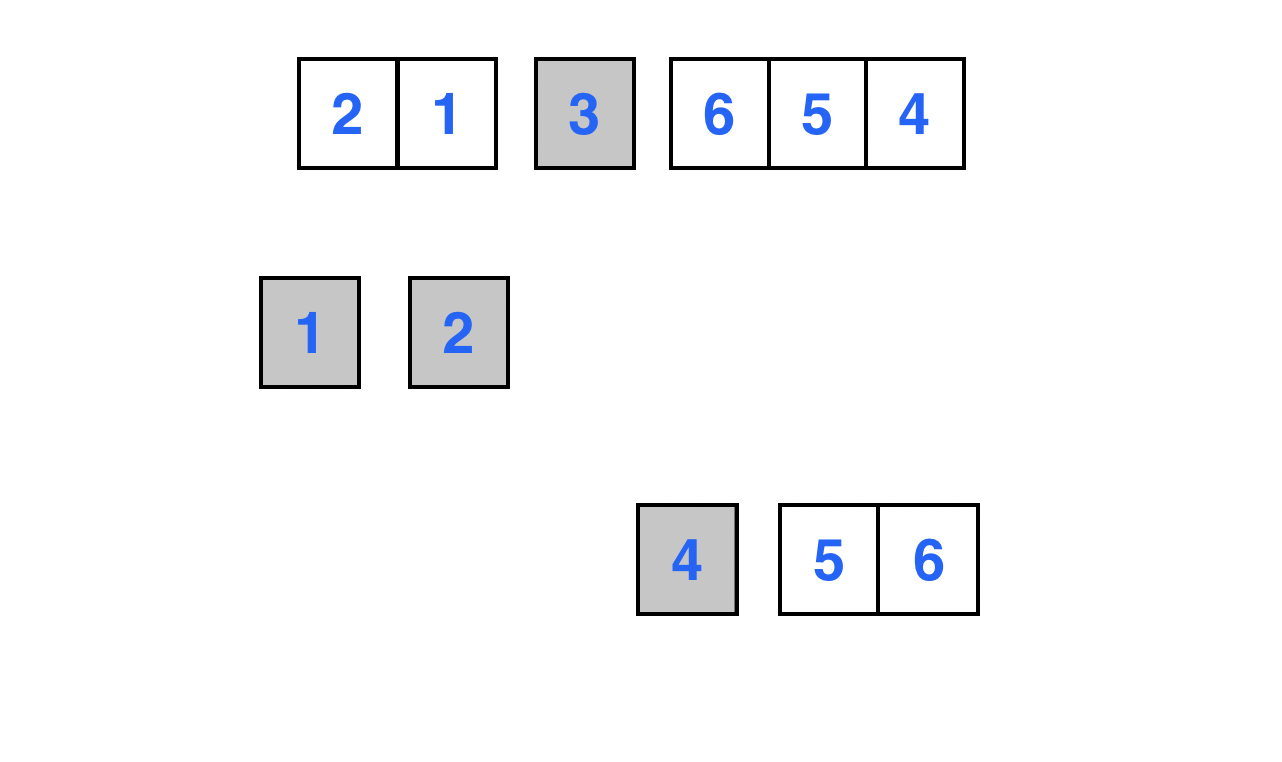
맨 마지막 원소를 피봇으로 선정한다.
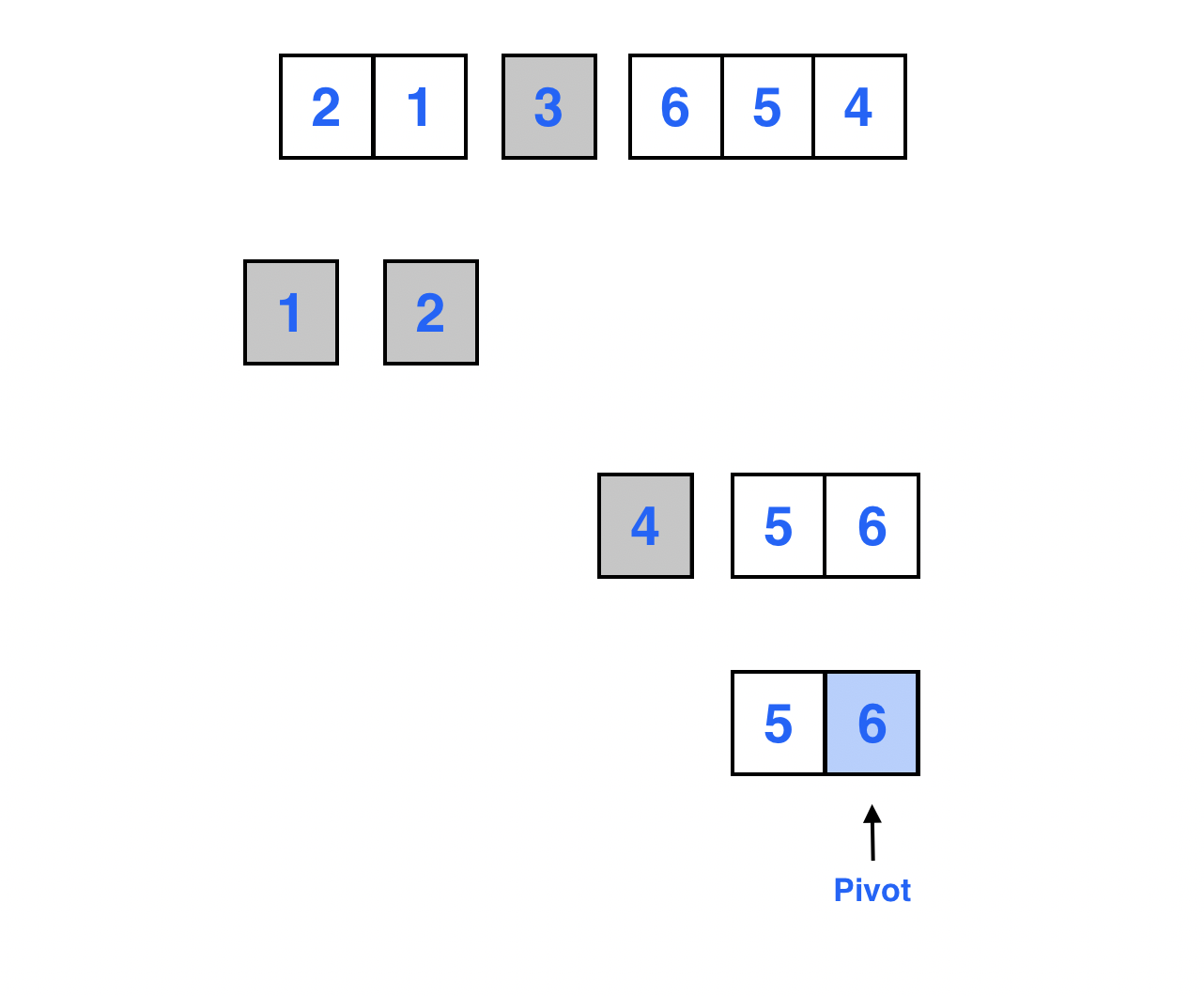
Left 포인터는 배열의 0 번째 인덱스를 가리키고, Right 포인터는 피봇 바로 앞의 원소를 가리킨다.
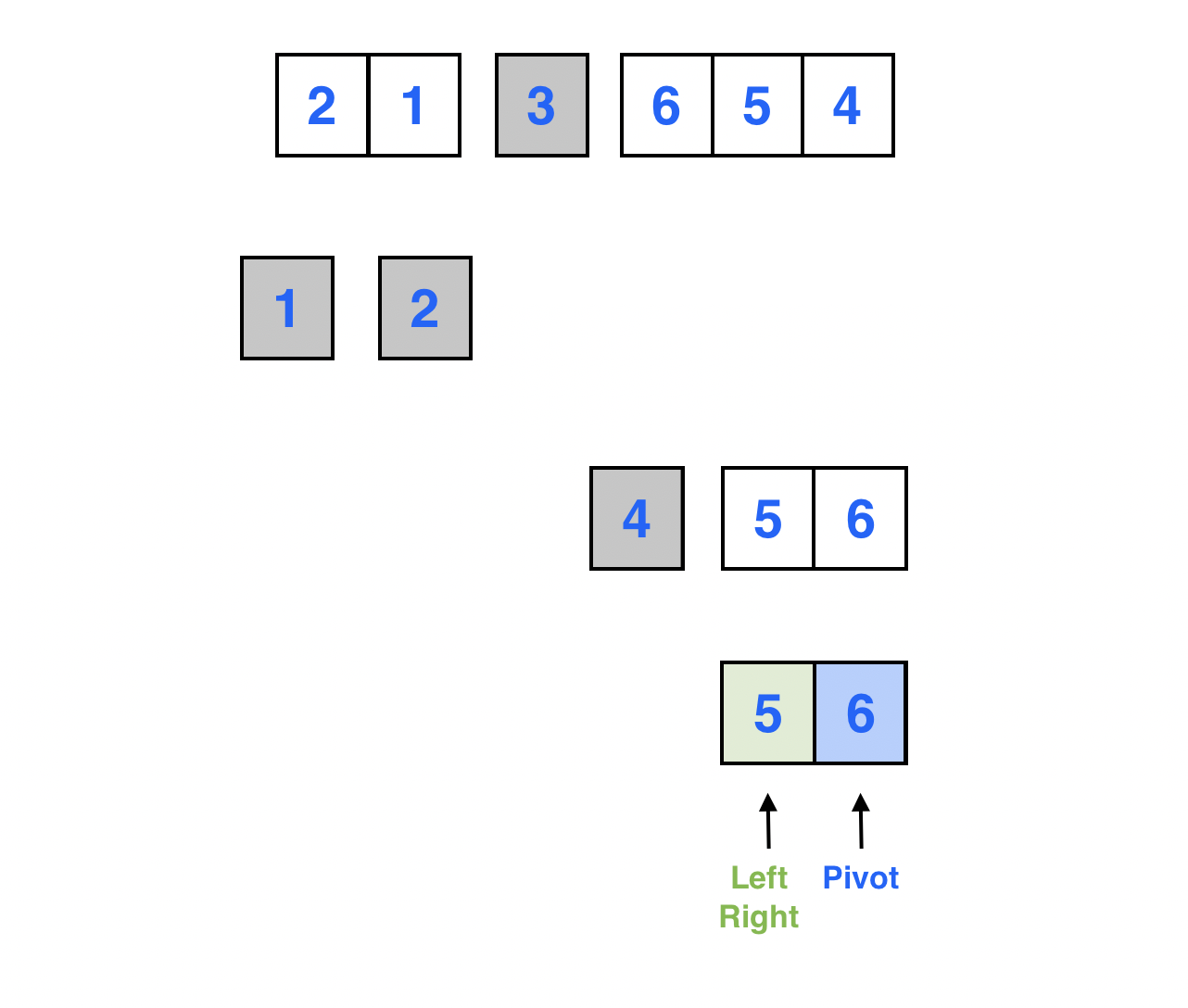
알고리즘에 의해 포인터를 움직인다.
Left > Right가 되었다.
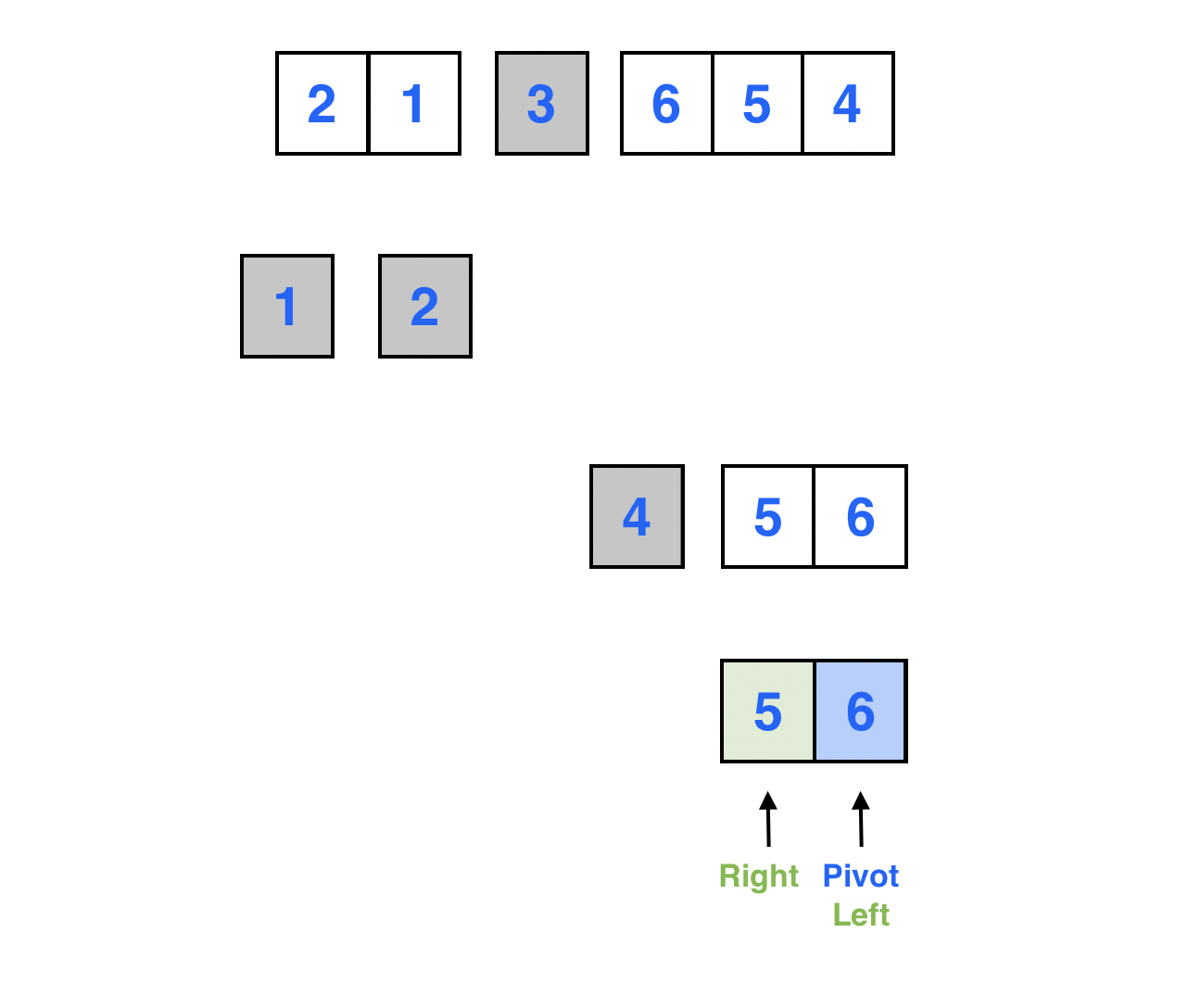
Left가 가리키는 원소와 피봇이 가리키는 원소를 서로 스왑한다.
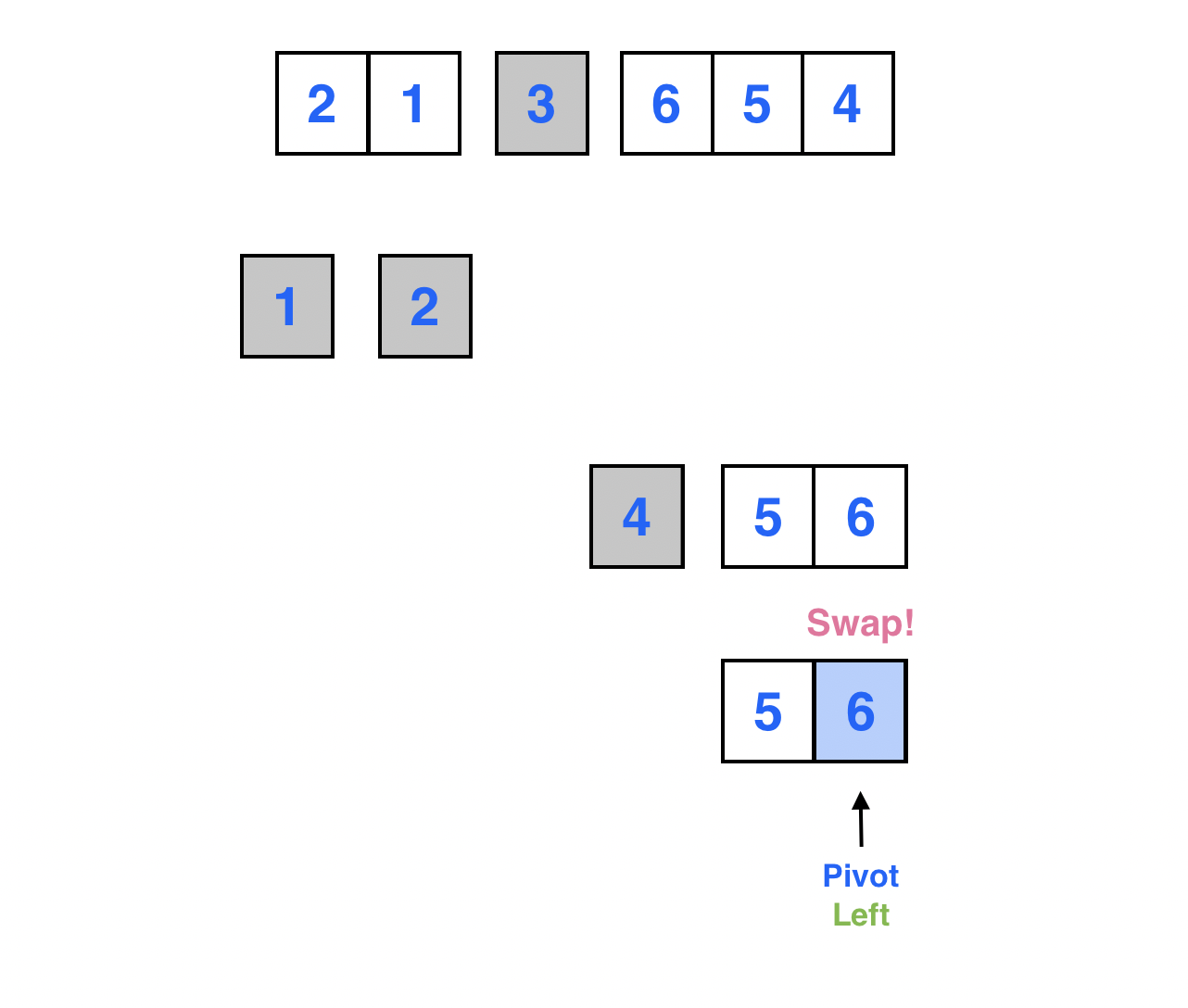
피봇이 가리키는 원소 6의 최종적인 위치가 정해진 모습이다.
원소 6을 기준으로 양 옆의 두 부분 배열은 모두 크기가 1 이하이므로 퀵소트를 수행하지 않는다.
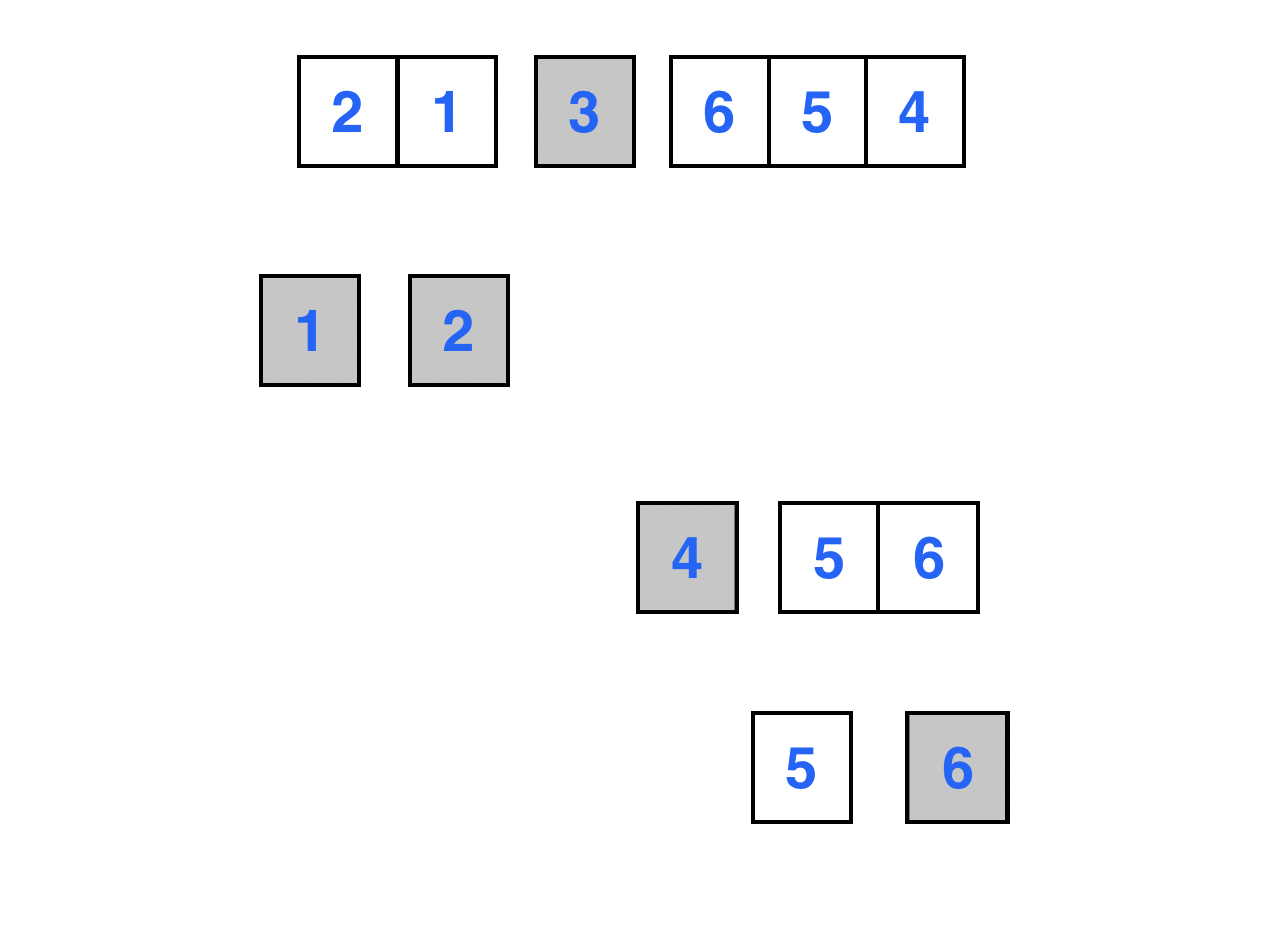
원소 5의 최종적인 위치가 정해진 모습이다.
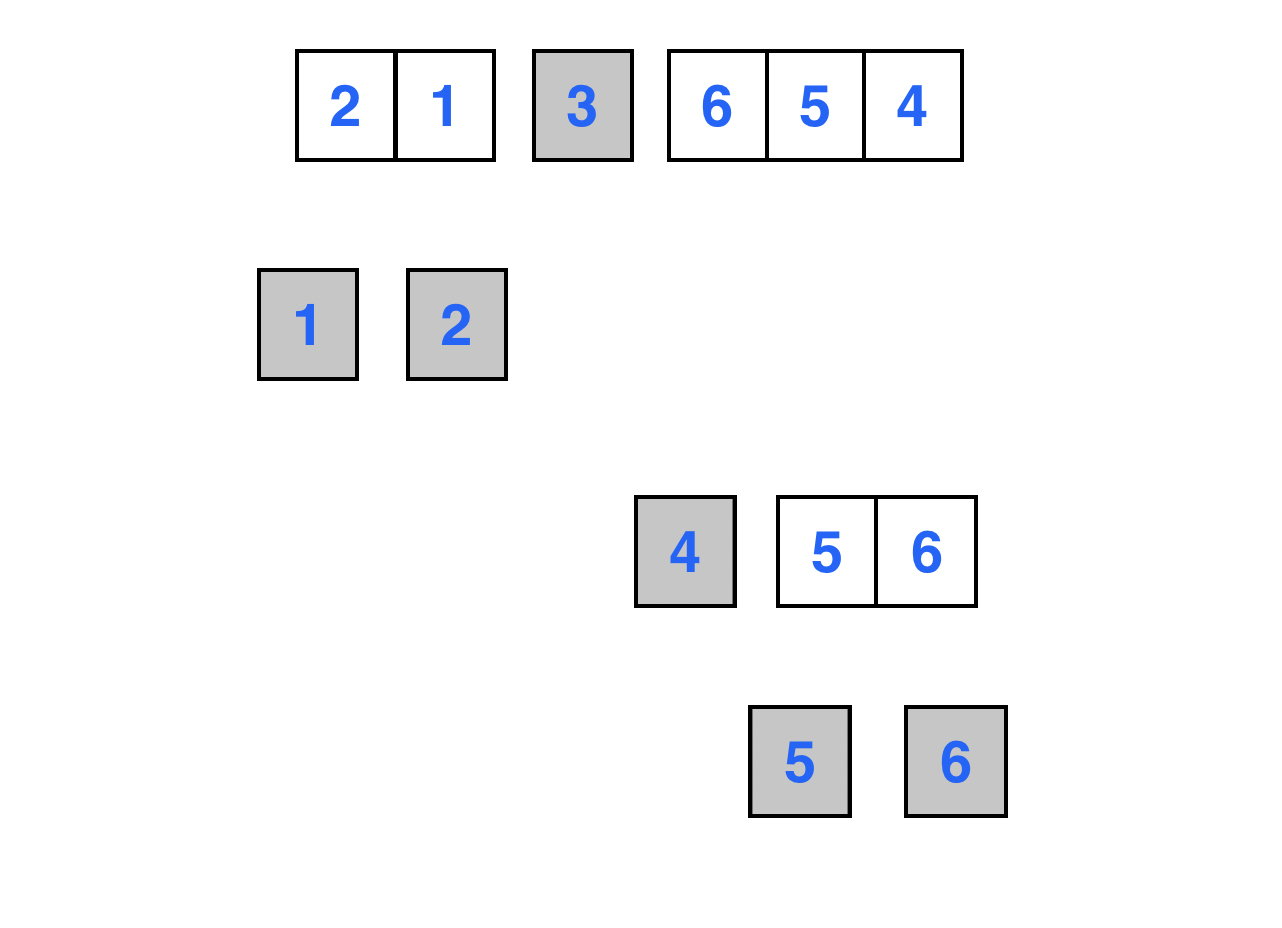
이로써 퀵 소트를 적용한 정렬이 완료된 모습이다.
Selecting pivot - Median of three
위 방법에서는 피봇을 선정할 때 배열의 맨 마지막 원소로 하였는데, 이렇게 되면 입력으로 이미 정렬이 완료된 배열이 들어왔을 때 최악의 성능을 내게 된다. 이를 방지하기 위한 방법은 의외로 간단한데, 피벗을 선정할 때 임의의 인덱스를 선정하거나 배열의 중간 인덱스를 피봇으로 선정하는 것이다.
보다 효율적인 방법은 세지윅(Sedgewick)이 제안한 것으로 세 개의 중앙값(Median of three)이 있다. 이것은 파티션의 첫번째 값, 중간값, 마지막 값의 중앙값(Median)을 계산하여 이를 피봇으로 선정하는 것이다.
이 세 개의 중앙값 방법은 이미 정렬이 되어있는 배열에 대해서는 아주 적절하며, 임의의 원소를 피봇으로 선정하는 방법보다 피봇을 선정하는데 있어 보다 최적의 추정을 하는 것으로 알려져 있다.
다음은 세 개의 중앙값(Median of three)의 의사코드이다.
mid := (lo + hi) / 2
if A[mid] < A[lo]
swap A[lo] with A[mid]
if A[hi] < A[lo]
swap A[lo] with A[hi]
if A[mid] < A[hi]
swap A[mid] with A[hi]
pivot := A[hi]
- lo : 첫번째 값
- hi : 마지막 값
- mid : 중간값
세 개의 값 중에서 제일 작은 값을 맨 앞(lo)으로 보낸다. 그리고 나머지 두개의 값을 비교해 중앙값을 계산한다. 이A[hi]중앙값을 피봇으로 사용한다.
임의의 피봇 선정 방법의 경우 $n$ 개의 요소를 정렬하는 데 필요한 예상 비교 수는 $1.386 nlogn$이다. 세 개의 중앙값은 예상 스왑 횟수가 3%정도 증가하는 대신 필요한 예상 비교 수를 1.188 n log n으로 낮춘다.
Implementation - java code
다음 코드는 퀵 소트를 자바로 구현한 것이다.
이 코드는 위 알고리즘을 적용하였으며, 피봇 선정은 세 개의 중앙값(Median of three)을 적용하였다.
/**
*
* This program is to sort an array using quick sort algorithm by ascending manner
* Applied Hoare partition scheme and median of three method as a pivot selecting
*
* This implementation is not stable sorting in which the relative position of
* two elements with the same value is preserved
*
* partition:
*
* Select a pivot using median of three method
* Arrange an element that less than or equal pivot key to the left side of pivot
* Arrange an element that greater than pivot key to the right side of pivot
*
* quickSort:
*
* recursively Sort left side and right side of pivot respectively
*
*
* Time Complexity:
*
* Average case performance: O(nlogn) where n is the number of item in an array
*
* Worst case performance: O(n^2)
*
* Best case performance: O(nlogn)
*
*
* Space complexity:
*
* Worst case space: O(n) auxiliary (naive)
*
* @author Gyeong
*
*/
import java.util.Arrays;
public class QuickSort {
public static void quickSort(int arr[], int start, int end){
if (start < end){
int pivot = partition(arr, start, end); // partition
quickSort(arr, start, pivot-1); // sort left side of pivot recursively
quickSort(arr, pivot+1, end); // sort right side of pivot recursively
}
}
public static int partition(int arr[], int start, int end){
int left = start;
int right = end-1;
// The median is placed at the end of the array. (end)
medianOfThree(arr, start, end);
// Pivot points to median
int pivot = end;
// Loop until left is less than or equal right
while (left <= right){
// Searching for the item that is greater than pivot item
while (left <= right && arr[left] <= arr[pivot])
left++;
// Searching for the item that is less than or equal pivot item
while (left <= right && arr[pivot] < arr[right])
right--;
// when right is less than left, sub array was sorted
if (left > right)
break;
// Elements smaller than the pivot are placed on the left side of pivot
// Elements larger than the pivot are placed on the right side of pivot
swap(arr, left, right);
left++;
right--;
}
// Arrange pivot item to the proper position of the array
swap(arr, left, pivot);
// return pivot index
return left;
}
// Find the median of three numbers and place it at the end of the array
public static void medianOfThree(int arr[], int left, int right){
// The smallest of the three numbers is placed before two numbers
int mid = (left+right)/2;
if (arr[mid] < arr[left])
swap(arr, mid, left);
if (arr[right] < arr[left])
swap(arr, right, left);
// then compare the second and third numbers to determine the median
if (arr[mid] < arr[right])
swap(arr, mid, right);
}
public static void swap(int arr[], int a, int b){
int temp = arr[a];
arr[a] = arr[b];
arr[b] = temp;
}
public static void main(String[] args) {
int arr[] = new int[]{2, 1, 4, 5, 7, 1, 1, 8, 9, 10, 11, 14, 15, 3, 2, 4};
System.out.println("Before sorting: " + Arrays.toString(arr));
quickSort(arr, 0, arr.length-1);
System.out.print("After sorting: " + Arrays.toString(arr));
}
}
Output:
Before sorting: [2, 1, 4, 5, 7, 1, 1, 8, 9, 10, 11, 14, 15, 3, 2, 4]
After sorting: [1, 1, 1, 2, 2, 3, 4, 4, 5, 7, 8, 9, 10, 11, 14, 15]
Time & Space Complexity
Quick sort
The worst-case performance : $O(n^2)$
The best-case performance : $O(nlogn)$ or $O(n)$ (세 개의 분할, 동일 원소 값)
The average-case performance : $O(nlogn)$
The worst-case space requirement : $O(n)$의 보조 공간
References
Quick sort - wikipedia
Quick sort - codingeek
Quick sort - programiz

Leave a comment