합병 정렬(Merge Sort)

Merge Sort(합병 정렬)

합병 정렬 또는 병합 정렬(merge sort)은 O(n log n) 비교 기반 정렬 알고리즘입니다.
일반적인 방법으로 구현했을 때 이 정렬은 안정 정렬에 속하며, 분할 정복 알고리즘의 하나입니다. 존 폰 노이만이 1945년에 개발했습니다.

Algorithm

밑의 애니메이션을 먼저 보시고 알고리즘을 읽으시면 이해가 빠를 수 있습니다.

1. 리스트의 길이가 1 이하이면 이미 정렬된 것으로 본다. 그렇지 않은 경우에는
2. 분할(divide) : 정렬되지 않은 리스트를 절반으로 잘라 비슷한 크기의 두 부분 리스트로 나눈다.
3. 정복(conquer) : 각 부분 리스트를 재귀적으로 합병 정렬을 이용해 정렬한다.
4. 결합(combine) : 두 부분 리스트를 다시 하나의 정렬된 리스트로 합병한다. 이때 정렬 결과가 임시배열에 저장된다.
5. 복사(copy) : 임시 배열에 저장된 결과를 원래 배열에 복사한다.

Animation - Merge sort

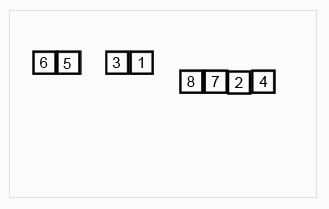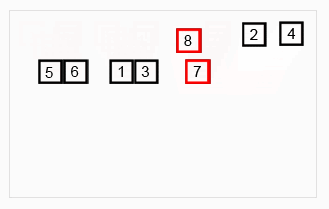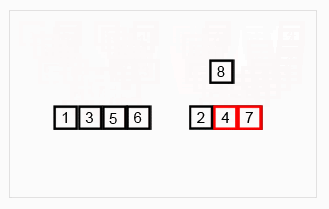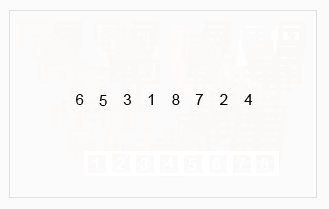
Analysis

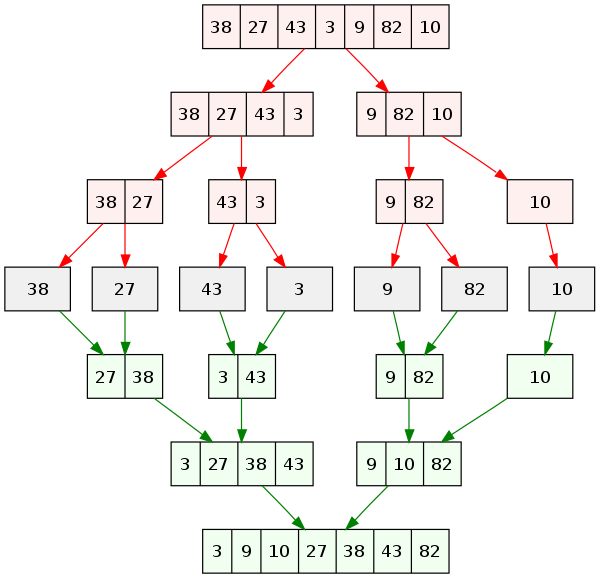
Note: 7개의 원소가 들어있는 배열에 재귀적 병합 정렬을 적용했을 때 우리가 상상할 수 있는 그림입니다.
배열의 원소가 1개가 될 때까지 원래 배열의 1/2씩 분할을 계속 진행합니다.
배열의 원소가 1개가 되면 병합을 진행합니다.
[38][27]
38은 27보다 크므로 두 원소가 스왑되어 합병됩니다.
[43][3]
43은 3보다 크므로 두 원소가 스왑되어 합병됩니다.
[27, 38] [3, 43]
27과 3이 스왑되고 38과 43은 그대로 배열에 들어갑니다.
이와 마찬가지로 다른 분할 배열들도 위와 같이 진행됩니다.

Java로 구현 - 재귀적(Top-down, Recursive)

설명: 재귀적으로 서브배열의 크기가 1이 될 때까지 계속 분할을 진행합니다.
분할된 배열들을 정렬하고 합병합니다.

// @author lemidia
public class MergeSort {
    static void divide(int data[], int p, int r){
        if(p < r){
            int q = (p+r)/2; // Middle
            divide(data, p, q); // Left
            divide(data, q+1, r); // Right
            merge(data, p, q, r); // Merge
        }
    }

    static void merge(int data[], int p, int q, int r){
        int i = p; int j = q+1; int k = p;
        int temp[] = new int[data.length];

        for (int l = p; l < r+1 ; l++) {
            if (i <= q && (j > r || data[i] < data[j])){
                temp[k++] = data[i++];
            }else
                temp[k++] = data[j++];
        }
        for(int l = p; l <= r; l++){
            data[l] = temp[l];
        }

        /*
        while (i<=q && j<=r){
            if(data[i] <= data[j]){
                temp[k++] = data[i++];
            }else{
                temp[k++] = data[j++];
            }
        }
        while (i<=q)
            temp[k++] = data[i++];
        while (j<=r)
            temp[k++] = data[j++];
        for(int l = p; l<=r; l++){
            data[l] = temp[l];
        }
        */

    }

    public static void main(String[] args) {
        int limit = 10;
        int arr[] = new int[limit];

        for(int i = limit-1; i >= 0; --i){
            arr[i] = limit-i;
        }
        divide(arr, 0, limit-1);
        for (int i = 0; i < arr.length; i++) {
            System.out.print(arr[i] + " ");
        }
    }
}

1 2 3 4 5 6 7 8 9 10 

시간복잡도

최악 시간복잡도	O(n log n)
최선 시간복잡도	O(n log n)
평균 시간복잡도	일반적으로, O(n log n)

쉬운 설명: 배열의 원소가 n개일 때 깊이는 log(n)만큼 진행 됩니다. (매번 2개씩 분할 되므로)
각 깊이마다 n개의 원소들이 제자리를 찾아 스왑됩니다.
그래서 시간복잡도는 깊이 * n개의 원소 즉, nlog(n)이 됩니다.

References

Merge Sort - wikipedia