에라토스테네스의 체(Eratosthenes’s Sieve)

에라토스테네스의 체

수학에서 에라토스테네스의 체는 보다 빠르게 소수를 찾는 방법입니다.
고대 그리스 수학자 에라토스테네스가 발견하였습니다.

---

선행지식: 수학에서 소수란?

소수: 1을 제외한 수 중에서 1과 자기 자신을 제외하고 약수를 가지지 않는 수를 말합니다.

예)

예1) 2는 1과 자기 자신(2)을 제외하고는 약수를 가지지 않습니다. 소수입니다.
예2) 5는 1과 자기 자신(5)을 제외하고는 약수를 가지지 않습니다. 소수입니다.
예3) 13은 1과 자기 자신(13)을 제외하고는 약수를 가지지 않습니다. 소수입니다.
예4) 15는 1과 자기자신(15)를 제외하고도 3, 5의 약수를 가집니다. 소수가 아닙니다.

Algorithm

밑의 애니메이션을 먼저 보시고 알고리즘을 읽으시면 이해가 빠를 수 있습니다.

1. 2부터 소수를 구하고자 하는 구간의 모든 수를 나열한다. 그림에서 회색 사각형으로 두른 수들이 여기에 해당한다.
2. 2는 소수이므로 오른쪽에 2를 쓴다. (빨간색)
3. 자기 자신을 제외한 2의 배수를 모두 지운다.
4. 남아있는 수 가운데 3은 소수이므로 오른쪽에 3을 쓴다. (초록색)
5. 자기 자신을 제외한 3의 배수를 모두 지운다.
6. 남아있는 수 가운데 5는 소수이므로 오른쪽에 5를 쓴다. (파란색)
7. 자기 자신을 제외한 5의 배수를 모두 지운다.
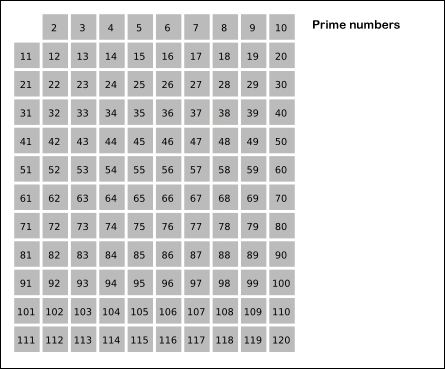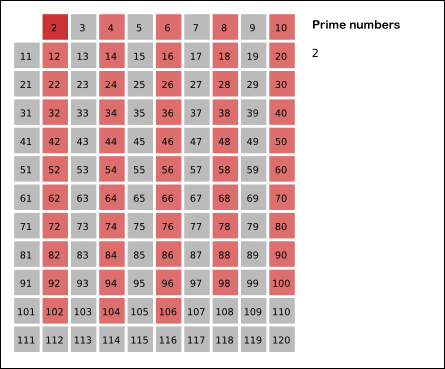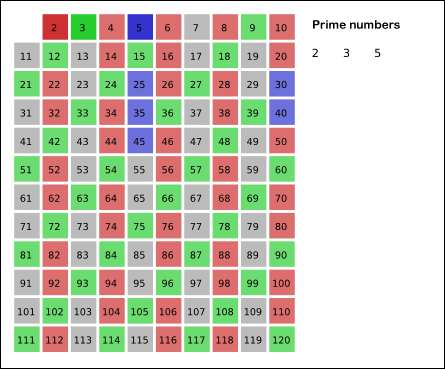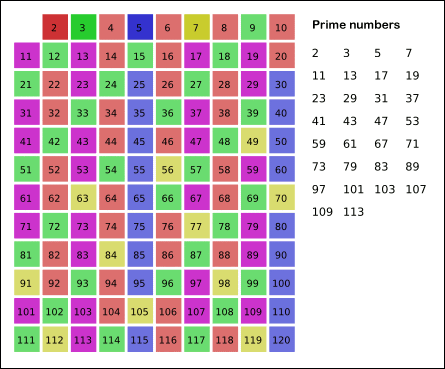
8. 남아있는 수 가운데 7은 소수이므로 오른쪽에 7을 쓴다. (노란색)
9. 자기 자신을 제외한 7의 배수를 모두 지운다.
10. 위의 과정을 반복하면 구하는 구간의 모든 소수가 남는다.

Note: 만약 x까지의 소수를 구한다고 하면 우리는 x까지 검사하여 일일히 지울 필요가 없습니다.
x는 >= $\sqrt {x}$ * $\sqrt {x}$으로 표현 할 수 있고, $\sqrt {x}$까지 수를 지우면, 그 이후의 수들은 이미 $\sqrt {x}$까지의 수에서 지워졋기 때문입니다.
예) x를 16 이라고 해봅시다. $\sqrt {x}$은 4 입니다.
8은 16의 약수입니다. 하지만 8은 이미 전 단계 2에서 지워졌습니다. 2 * 8이기 때문입니다.
예제에서는 120까지 구하고 있으므로 120의 제곱근 $\sqrt {120}$ = 10까지만 지워도 됩니다.
왜냐하면 $\sqrt {120}$ = 10 이후의 배수들은 이미 전 단계에서 지워졋기 때문입니다.

Java로 구현

import java.util.Arrays;

public class Eratosthenes {
    private static final int MAX = 30;

    public static void main(String[] args) {

        boolean [] flag = new boolean[MAX];
        Arrays.fill(flag, true);
        eratosthenes(flag, MAX);
        for (int i = 2; i < flag.length; i++){
            if (flag[i]){
                System.out.println(i + " is prime number");
            }
        }
    }

    public static void eratosthenes(boolean[] flag, int k){
        for (int i = 2; i*i < k ; i++) {
            if (flag[i]){
                for (int j = i*i; j < k ; j+=i) {
                    flag[j] = false;
                }
            }
        }
    }
}

2 is prime number
3 is prime number
5 is prime number
7 is prime number
11 is prime number
13 is prime number
17 is prime number
19 is prime number
23 is prime number
29 is prime number

References

Eratothenes - wikipedia