Graph 글 참고하기

Graph

Queue 글 참고하기

Queue

SPFA(Shortest Path Faster Algorithm)

The Shortest Path Faster Algorithm (SPFA)는 Bellman–Ford algorithm 을 개선한 알고리즘 으로서, 방향 가중치 그래프에서 단일 출발 정점 최단 거리를(Single source shortest path distance) 계산한다. 다른 여타 Bellman–Ford algorithm 이나 Dijkstra’s algorithm 과 같은 Single source shortest path algorithm 처럼 SPFA도 변 경감(Edge relaxation)을 핵심 연산으로 하여 동작한다.

이 SPFA는 무작위 희소 그래프에서 잘 동작한다고 알려져 있고, 음수 가중치 간선(Nagative weighted edge)을 가진 그래프에서도 적합하다. 그러나 최악 시간복잡도는 $O(|V|\cdot|E|)$ 로서 Bellman–Ford algorithm과 같기 때문에, 음수 가중치 간선이 없는 그래프의 경우에는 최악 시간복잡도를 고려한다면 Dijkstra’s algorithm이 더 적합하다고 볼 수 있다.

Algorithm

방향 가중치 그래프가 주어지고 $G = (V, E)$ 그리고 출발 정점을 $s$라고 하자. SPFA는 출발 정점 $s$으로부터 다른 모든 정점 $v$로의 최단 경로를 찾는다. $s$로 부터 $v$로의 최단 경로 거리는 각 정점 $v$에 대하여 $d(v)$에 저장된다.

SPFA는 각 정점의 인접 정점을 필요하다면 변 경감(Edge relaxation)하기 위해 각 정점을 후보자로 사용한다. 이 점은 Bellman–Ford algorithm과 같다. 하지만 Bellman–Ford algorithm과 비교했을 때의 개선점은 모든 정점들을 무조건 적으로 연산을 시도하기 보다는 SPFA는 후보자 정점에 대한 Queue를 가지고, 어떤 정점에 대해 그 정점이 변 경감 연산이 이루어졌을 때만 후보자 정점으로서 Queue에 삽입을 한다. 이런 행동들은 변 경감 연산이 실행될 정점이 없을 때까지 반복된다.

다음은 SPFA의 의사코드이다.

Input: 그래프 G, 시작 정점 s

$Q$는 변 경감 연산이 되고 난 후의 후보자를 담을 Queue를 의미한다.
$w(u,v)$는 간선 $(u,v)$의 간선 가중치를 의미한다.

Notice: Q 안에 v의 존재 유무를 판단하기 위해 구현 시에는 이를 추적하기 위한 추가적인 자료구조가 요구된다.

procedure Shortest-Path-Faster-Algorithm(G, s)
  for each vertex v ≠ s in V(G)
      d(v) := ∞
  d(s) := 0
  offer s into Q
  while Q is not empty
      u := poll Q
      for each edge (u, v) in E(G)
          if d(u) + w(u, v) < d(v) then
              d(v) := d(u) + w(u, v)
              if v is not in Q then
                  offer v into Q

하나씩 보자.

1    for each vertex v ≠ s in V(G)
2        d(v) := ∞

그래프 G의 출발 정점 s를 제외한 모든 정점 v에 대하여 s로부터 각 v에 대한 최단경로 거리 d(v)를 INF로 초기화 한다.

 3    d(s) := 0
 4    offer s into Q

먼저 출발 정점 s의 최단경로 거리를 0으로 초기화하고 s를 Q에 넣는다.

5    while Q is not empty

큐가 빌 때 까지 아래 연산들을 반복한다.

6    u := poll Q
7    for each edge (u, v) in E(G)

Q에서 정점하나를 꺼내 u라 하고, 그래프 G에서 u와 인접한 정점 v와의 간선 (u, v)에 대하여

8    if d(u) + w(u, v) < d(v) then
9       d(v) := d(u) + w(u, v)

s로부터 u로의 최단경로 거리 d(u) + 간선 (u, v)의 값이 s로부터 v로의 최단경로 거리 d(v)보다 작다면 d(v)값을 d(u) + w(u, v)로 업데이트 한다. (Edge Relaxation)

10      if v is not in Q then
11          offer v into Q

변 경감 연산(Edge Relaxation)이 된 정점 v가 현재 Q에 없으면, v를 Q에 추가한다.

Step by step

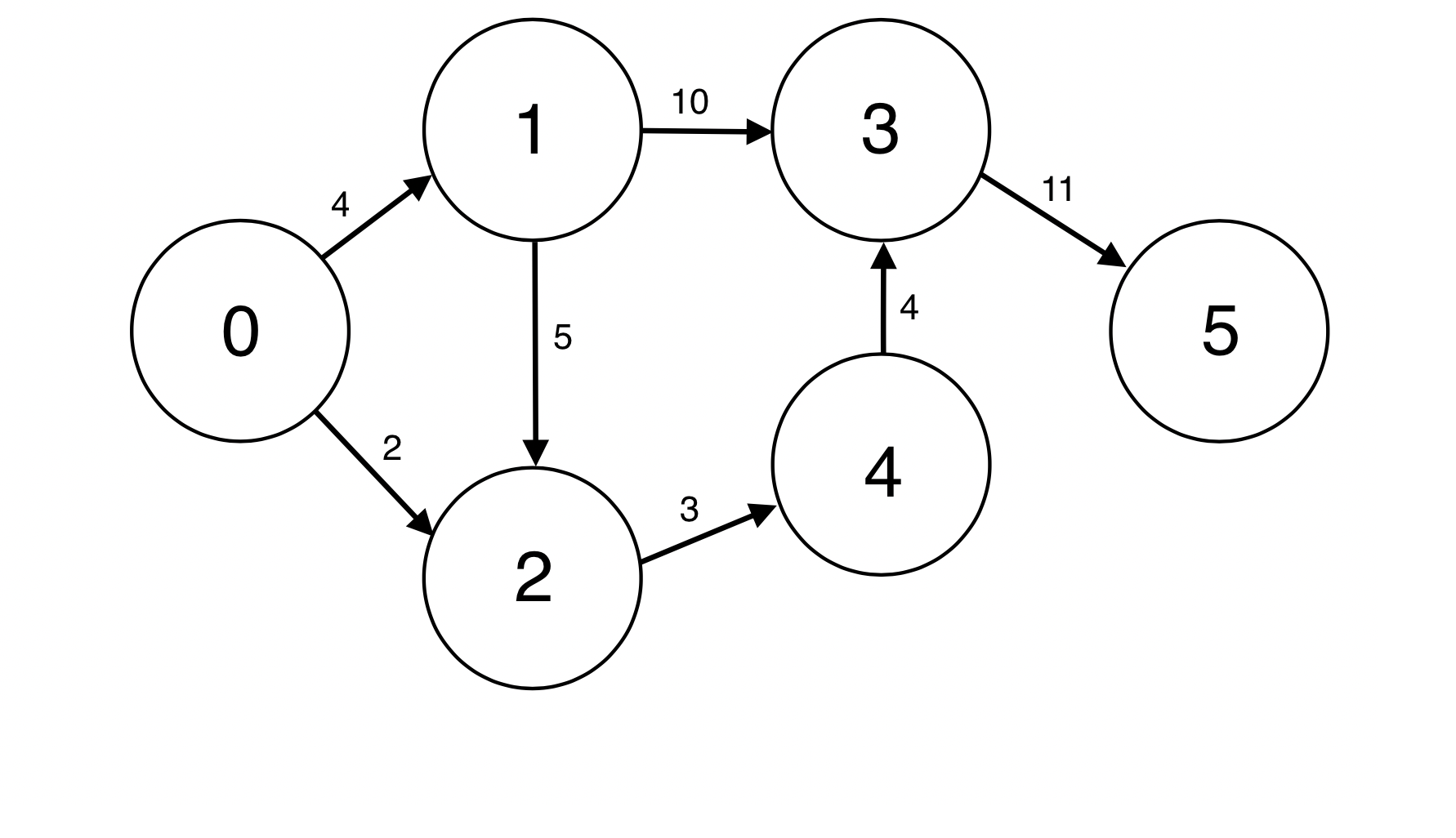
실제 그래프를 예로 들어 SPFA가 어떻게 동작하는지 알아보자.

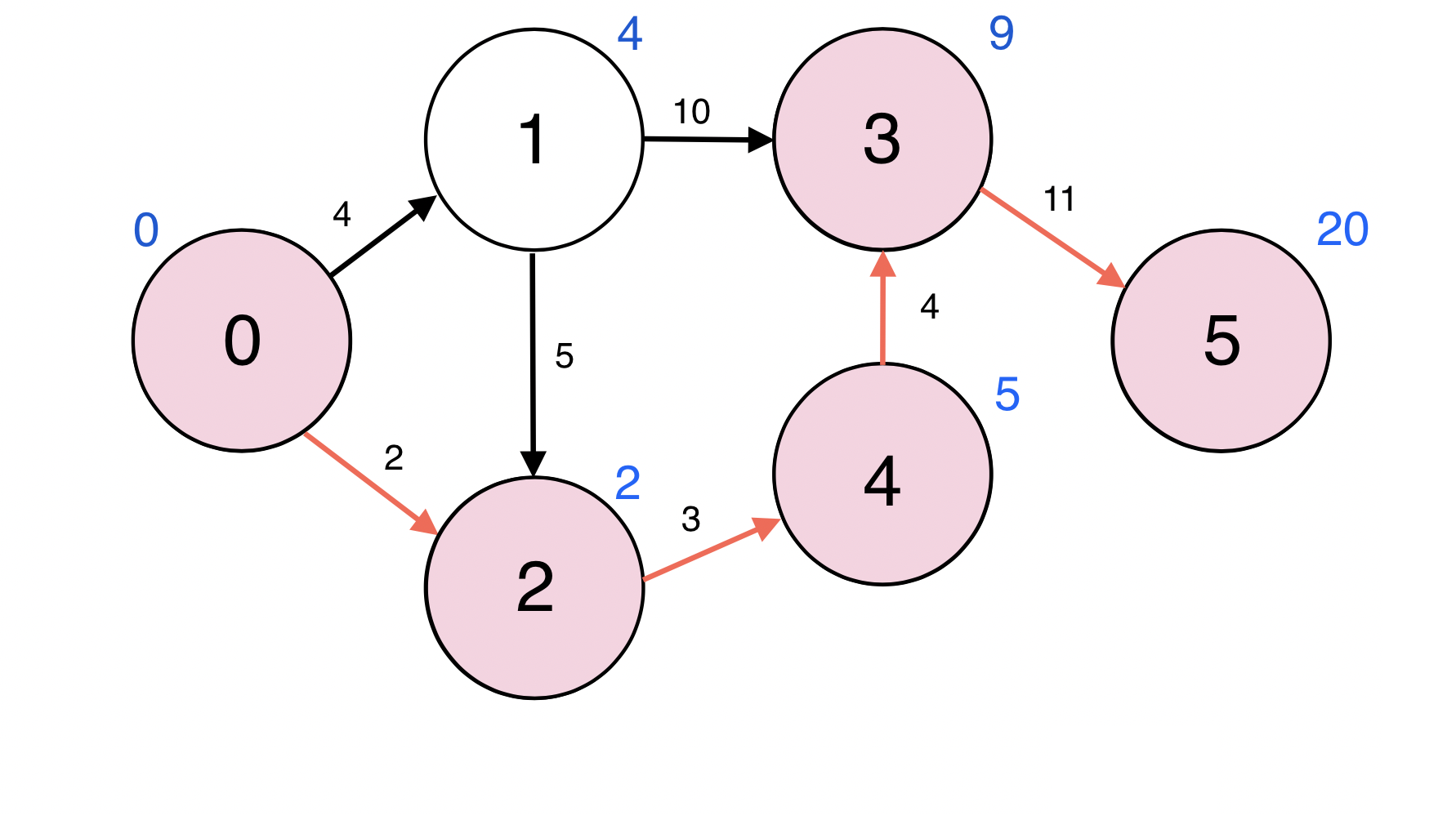
0번을 시작 정점으로 하여 5번 정점으로의 최단 경로를 구한다.

해당 정점에 연결된 인접 정점이 여러개 일 땐, 번호가 작은 것을 먼저 선택한다.

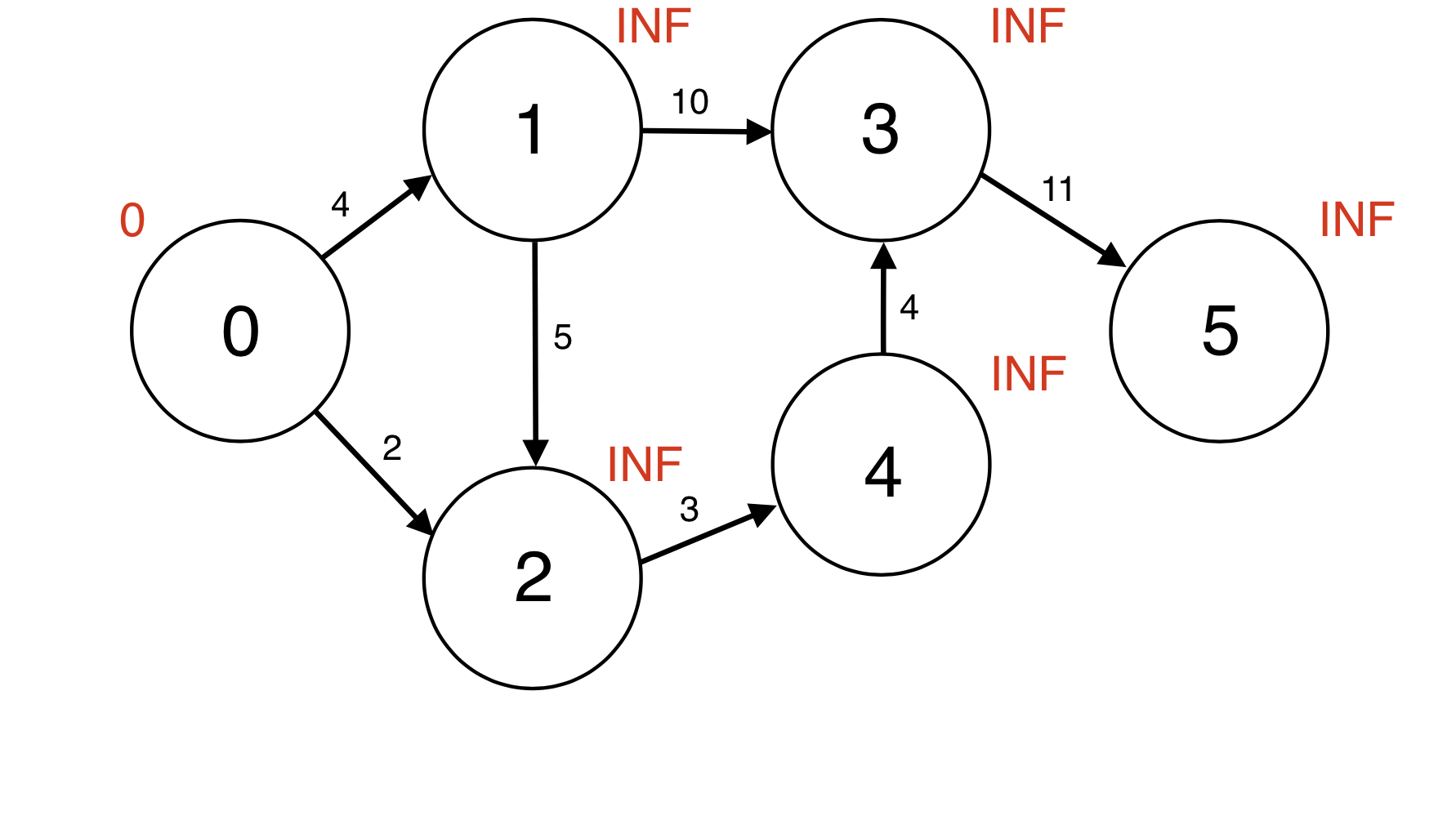
Alt text

시작 정점으로 부터 모든 정점까지의 최단거리 d(v)를 무한대(INF)로 초기화 한다.
d(s)는 0으로 초기화 한다.

Queue에 시작 정점 0을 넣는다.
Queue : [0]

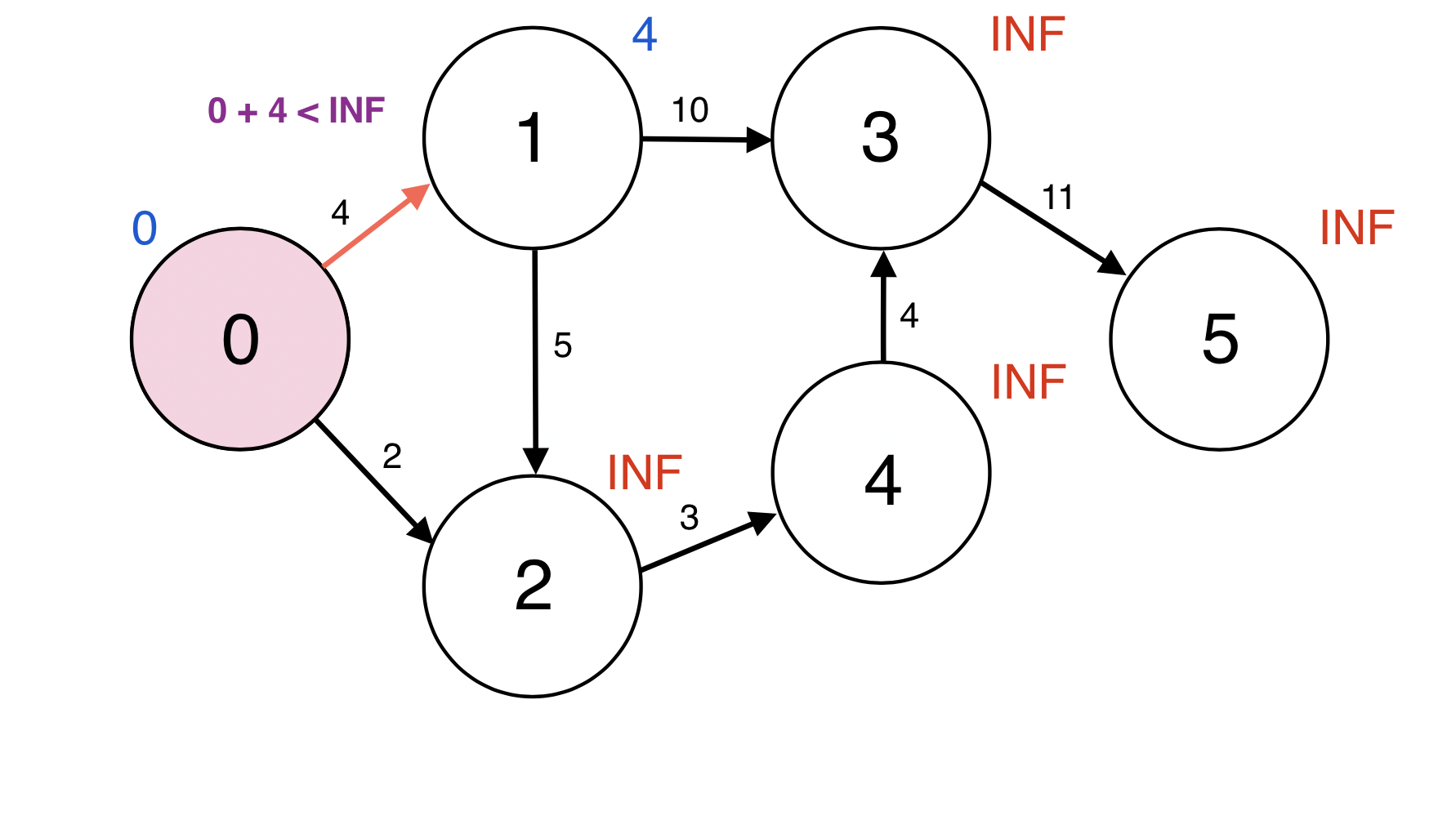
Alt text

Queue에서 원소 하나를 pop한다.
0번 정점과 인접한 정점 1번에 대하여 d(0) + w(0, 1) < d(1): 0 + 4 < INF이므로 d(1)을 4로 업데이트 한다.

업데이트 되었으므로 1번 정점을 Queue에 넣는다.
Queue : [1]

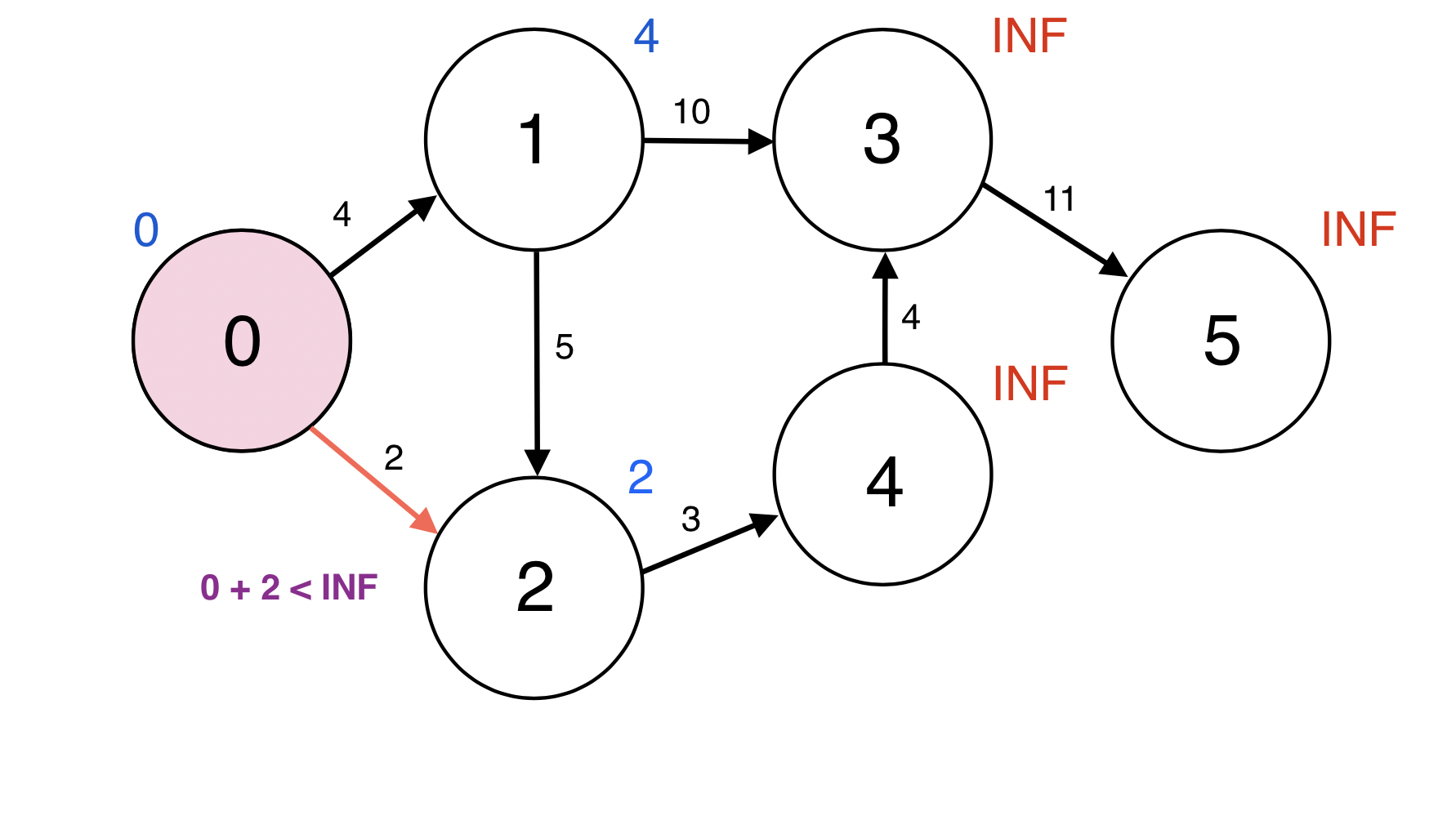
Alt text

0번 정점과 인접한 정점 2번에 대하여 d(0) + w(0, 2) < d(1): 0 + 2 < INF이므로 d(2)을 2로 업데이트 한다.

업데이트 되었으므로 2번 정점을 Queue에 넣는다.
Queue : [1 2]

Alt text

Queue에서 원소 하나를 pop한다.
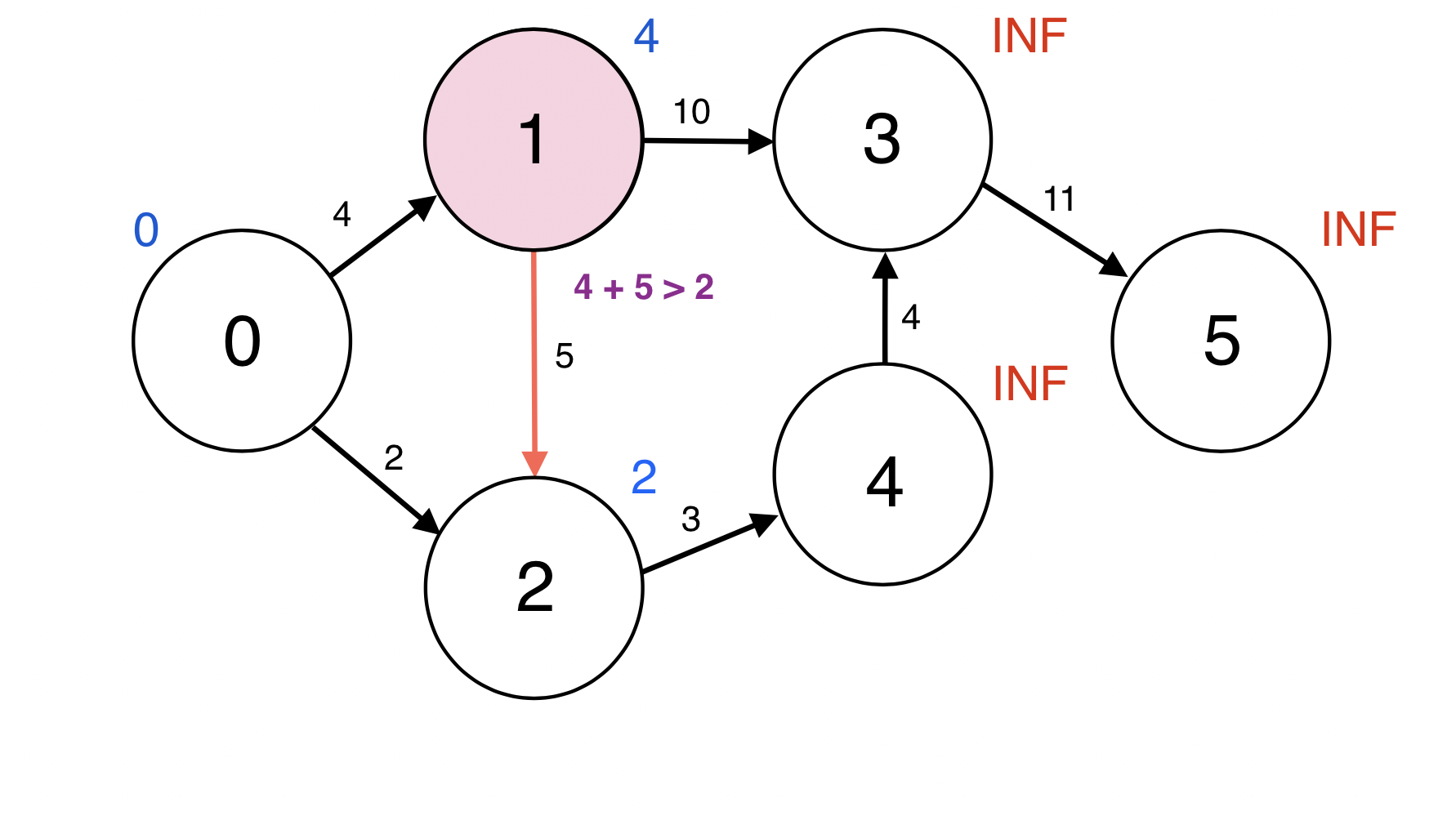
1번 정점과 인접한 정점 2번에 대하여 d(1) + w(1, 2) < d(2): 4 + 5 > 2이므로 d(2)를 업데이트 하지 않는다.

Queue : [2]

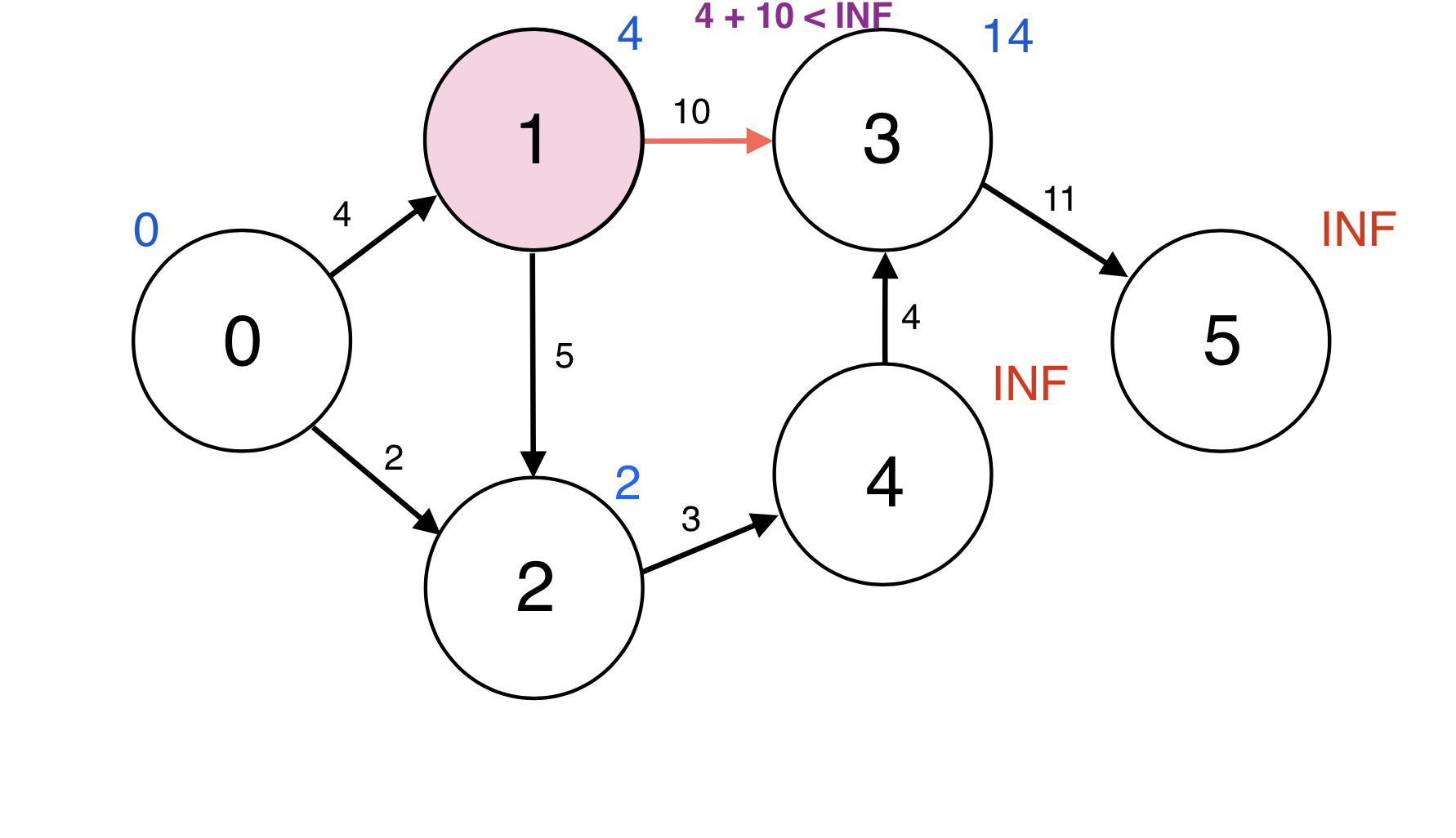
Alt text

1번 정점과 인접한 정점 3번에 대하여 d(1) + w(1, 3) < d(3): 4 + 10 < INF이므로 d(3)을 14로 업데이트 한다.

업데이트 되었으므로 3번 정점을 Queue에 넣는다.
Queue : [2, 3]

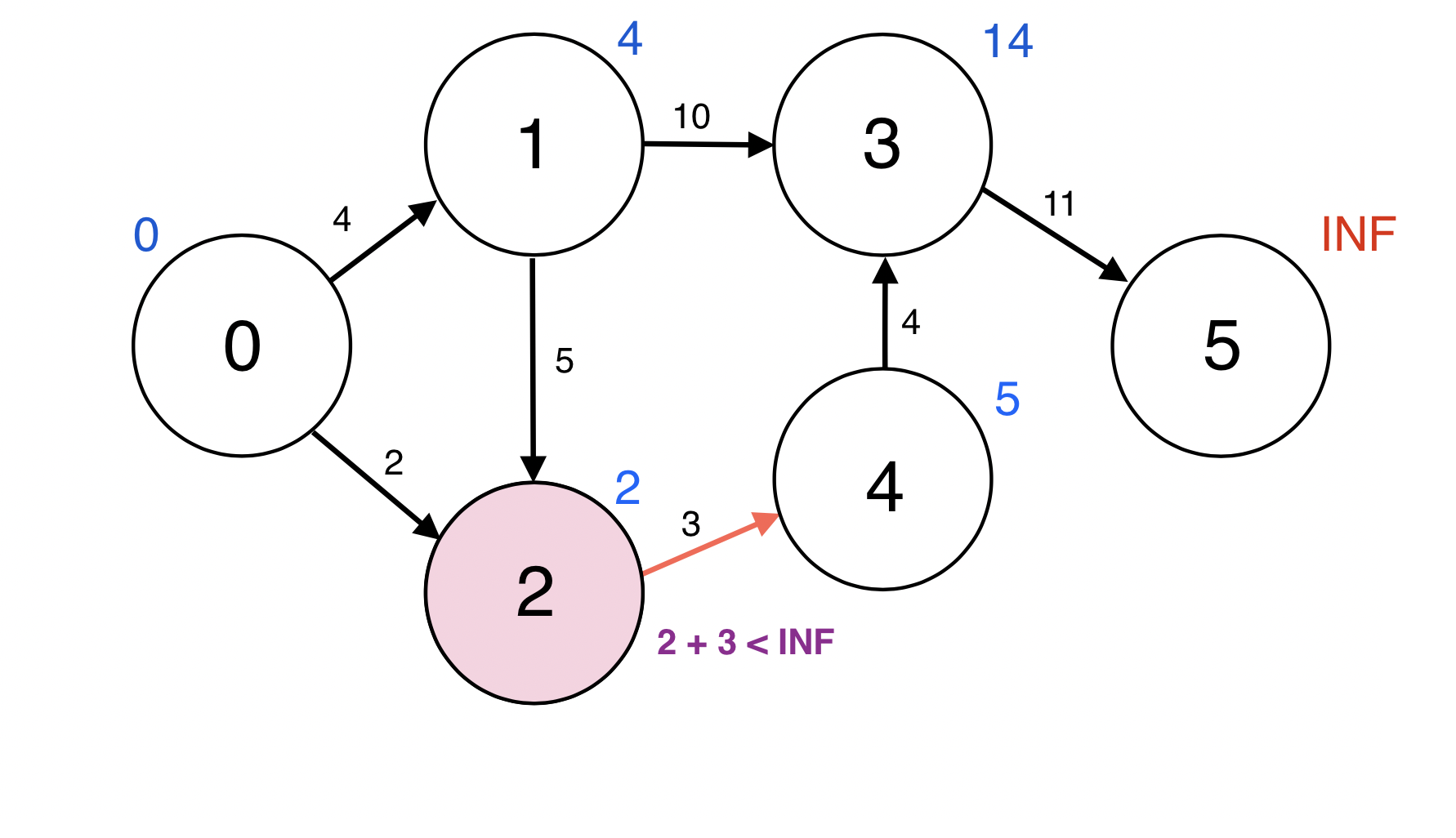
Alt text

Queue에서 원소 하나를 pop한다.
2번 정점과 인접한 정점 4번에 대하여 d(2) + w(2, 4) < d(4): 2 + 3 < INF이므로 d(4)을 5로 업데이트 한다.

업데이트 되었으므로 4번 정점을 Queue에 넣는다.
Queue : [3, 4]

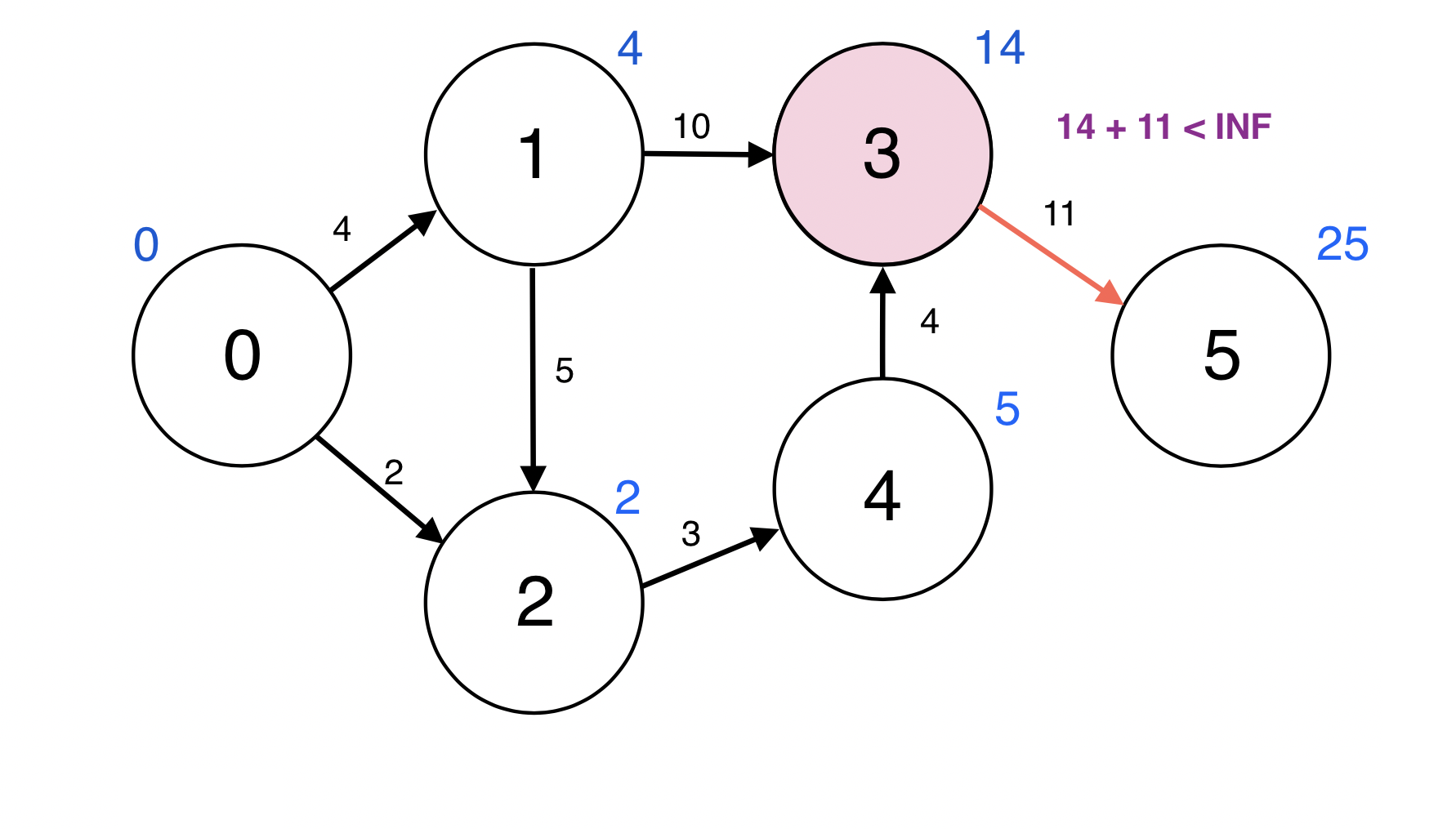
Alt text

Queue에서 원소 하나를 pop한다.
3번 정점과 인접한 정점 5번에 대하여 d(3) + w(3, 5) < d(5): 14 + 11 < INF이므로 d(5)을 25로 업데이트 한다.

업데이트 되었으므로 5번 정점을 Queue에 넣는다.
Queue : [4, 5]

Alt text

Queue에서 원소 하나를 pop한다.
4번 정점과 인접한 정점 3번에 대하여 d(4) + w(4, 3) < d(3): 5 + 4 < 14이므로 d(3)을 9로 업데이트 한다.

업데이트 되었으므로 3번 정점을 Queue에 넣는다.
Queue : [5, 3]

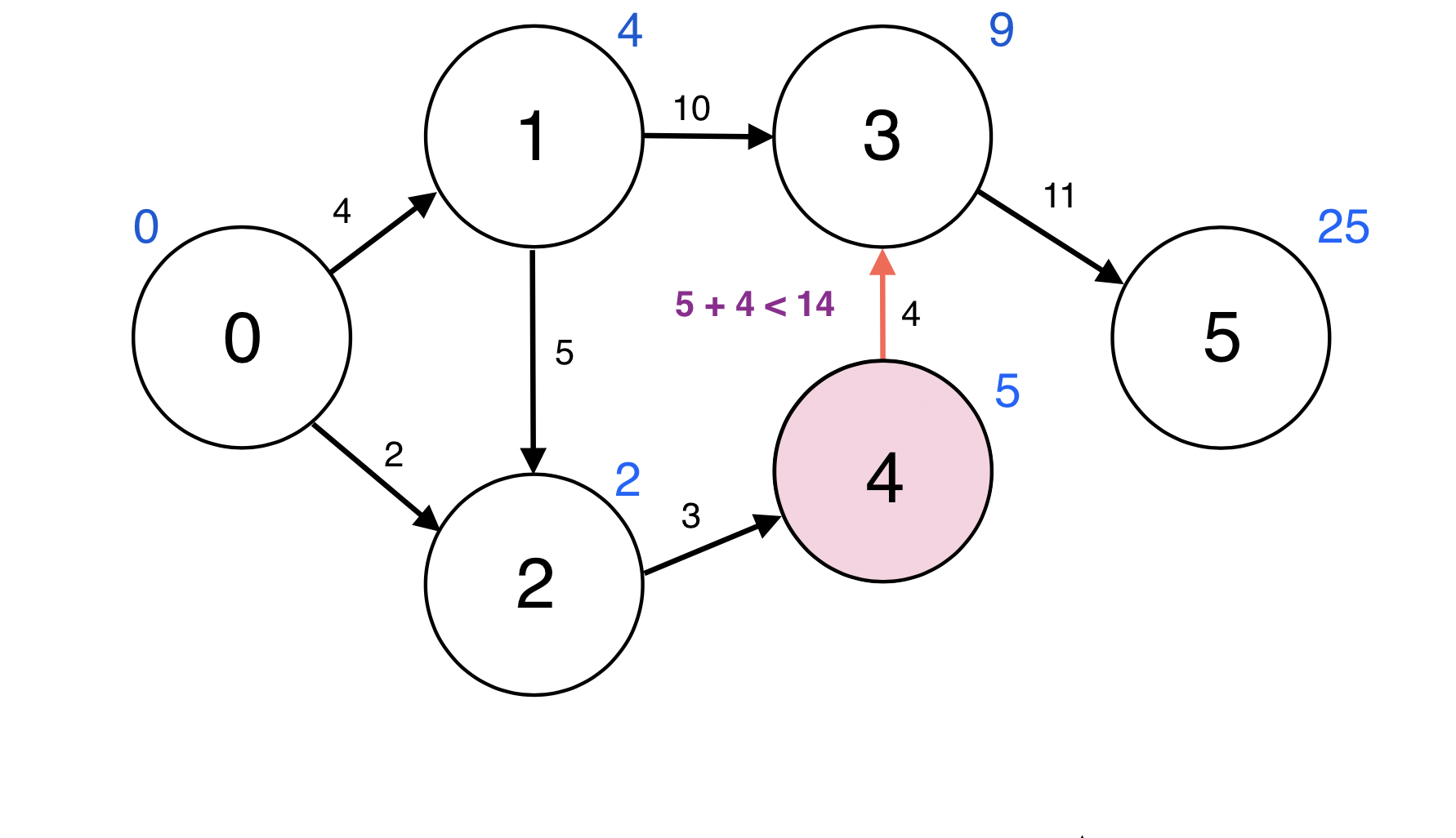
Alt text

Queue에서 원소 하나를 pop한다.
5번 정점과 인접한 정점이 없다.

Queue : [3]

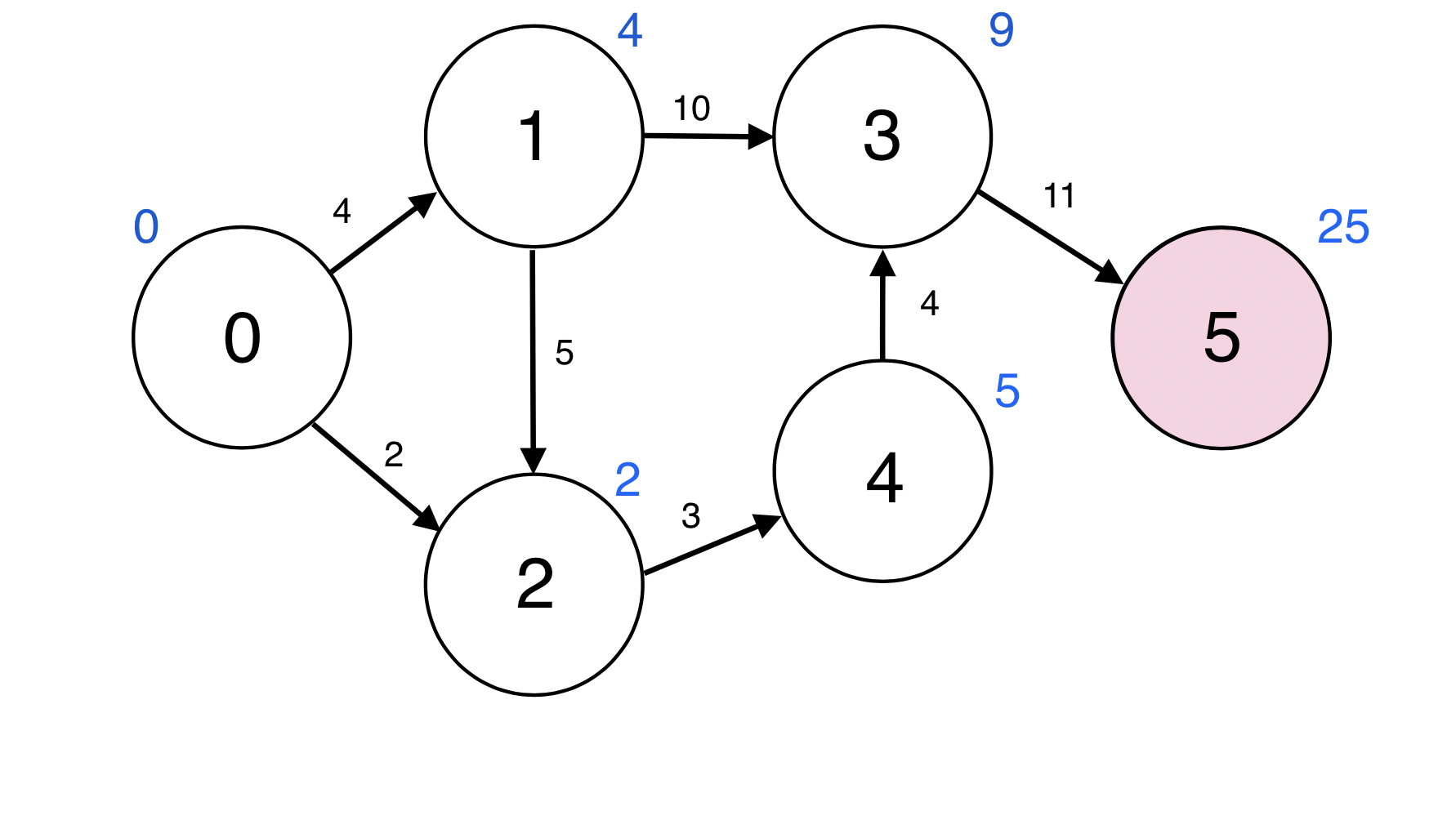
Alt text

Queue에서 원소 하나를 pop한다.
3번 정점과 인접한 정점 5번에 대하여 d(3) + w(3, 5) < d(5): 9 + 11 < 25이므로 d(5)을 20로 업데이트 한다.

업데이트 되었으므로 5번 정점을 Queue에 넣는다.
Queue : [5]

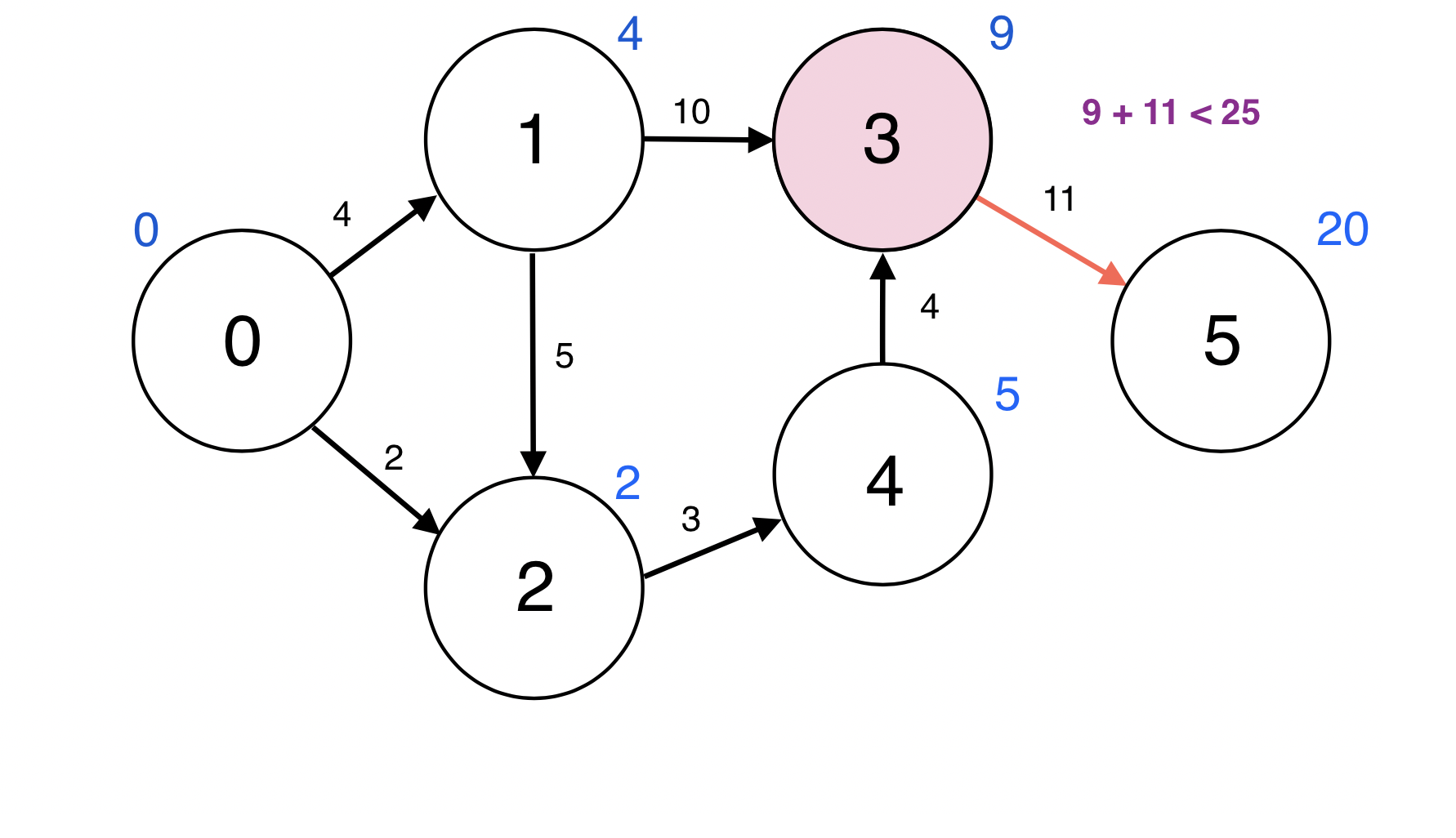
Alt text

Queue에서 원소 하나를 pop한다.
5번 정점과 인접한 정점이 없다.

Queue : [ ]

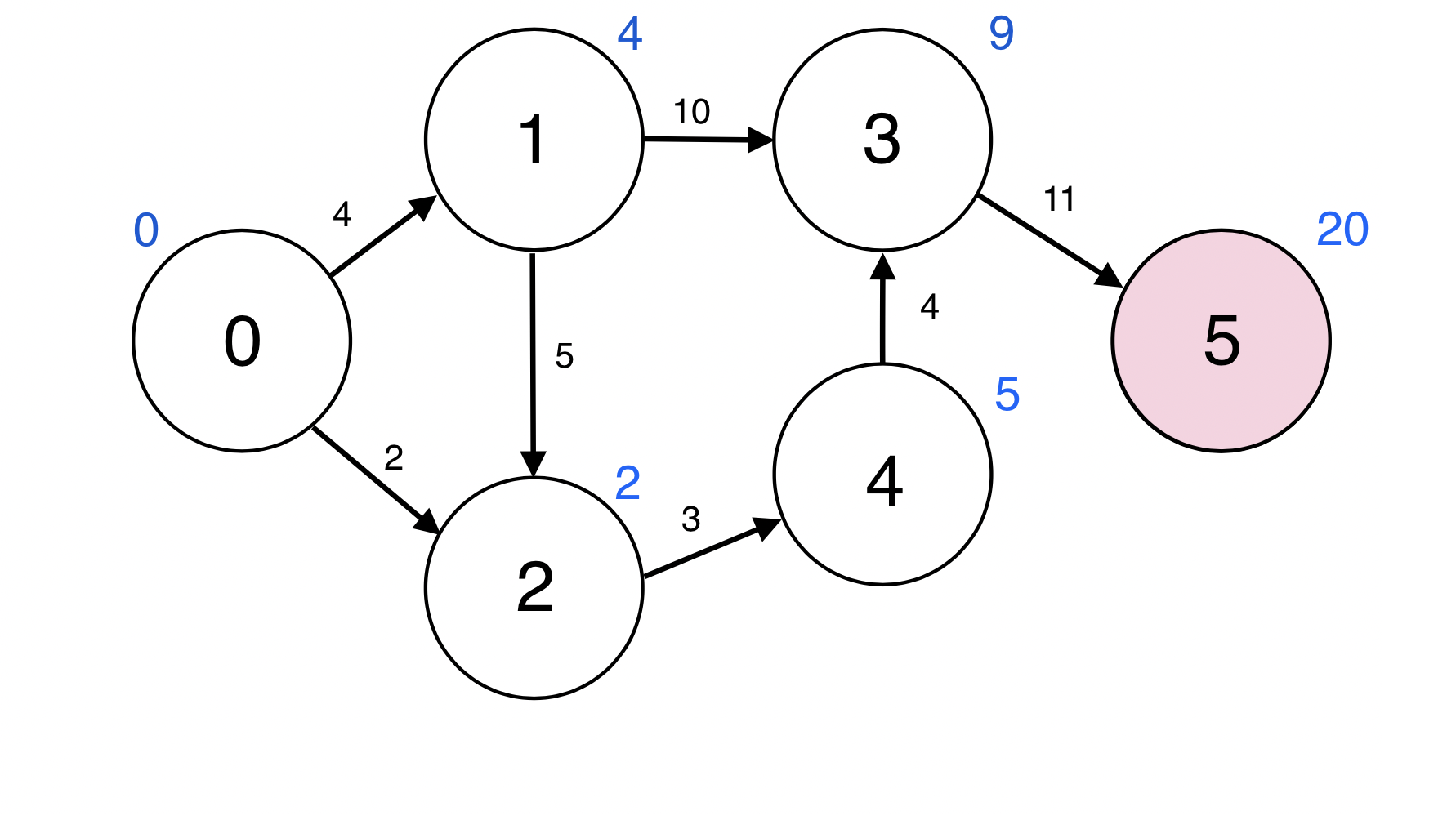
Alt text

큐가 비었으므로 SPFA가 완료되었다.

0번 부터 5번으로의 최단경로는 빨간선을 따라간 경로이고 그 거리는 20이다.

Alt text

Implementation

다음은 위 의사코드를 바탕으로 SPFA를 구현한 자바 메소드이다.

static void shortestPathFasterAlgorithm(int s){
    dist = new int[n];
    onQueue = new boolean[n];
    Arrays.fill(dist, INF);
    Queue<Integer> queue = new LinkedList<>();
    queue.offer(s);
    dist[s] = 0;
    onQueue[s] = true;
    while (!queue.isEmpty()){
        int cur = queue.poll();
        onQueue[cur] = false;
        for (Edge e : graph[cur]){
            if (dist[cur] + e.cost < dist[e.to]){
                dist[e.to] = dist[cur] + e.cost; // Edge Relaxation
            }
        }
    }
}

현재 Queue에서 정점 $v$의 존재 유무를 추적하기 위해 위 코드에서는 onQueue[] 를 사용한다.

그래프의 가중치 간선 정보를 구성하기 위해 아래의 Edge 클래스를 사용한다.

to는 다음 인접 정점의 번호, cost는 간선 비용(가중치)를 나타낸다.

...
// static ArrayList<Edge> [] graph;
...

static class Edge{
    int to;
    int cost;

    // Constructor
    public Edge(int to, int cost) {
        this.to = to;
        this.cost = cost;
    }
}

다음은 SPFA를 구현한 자바 코드이다.

그래프의 입력은 예제 그래프를 사용하였고, 최단경로를 추적하고 구성하기 위해 pred[]배열을 선언한 뒤 SPFA의 실행 중에 어느 한 포인트에서 정점 u, v가 있고(정점 v가 u에 의해 relaxation 되어지는 정점), relaxation 되어진 정점 v가 있으면, 그 정점을 relaxation하게 만든 정점 u가 최단경로 상의 이전 노드 이므로 pred[e.to] = cur;를 하여 경로를 구축한다. 그 다음 printPathReconstruction함수로 경로를 출력한다.

이 프로그램은 최단경로 거리와 그 경로를 출력한다.

Input: Graph G, start vertex
Output: Distance of shortest path of Graph G, shortest path of Graph G

시작 정점은 0번이다.

import java.io.*;
import java.util.*;
import java.util.LinkedList;

/**
 * This program is to find Shortest path in weighted graph using SPFA.
 * Time Complexity : Worst case : O(VE) same as Standard Bellman ford
 *                   Average case : O(E) - not proved
 *
 * @author Lemidia(Gyeong)
 */

public class ShortestPathFasterAlgorithm{

     // the number of vertices in Graph G
    static int n;
    // Shortest distance from s to each vertex v
    static int dist[];
    // for construct shortest path
    static int pred[];
    static ArrayList<Edge> [] graph;
    static final int INF = Integer.MAX_VALUE;
    // For check whether the vertex is on queue or not
    static boolean onQueue[];


    // Init Graph G
    static void createGraph(){
        graph = new ArrayList[n];
        for (int i = 0; i < n; i++){
            graph[i] = new ArrayList<>();
        }
    }

    // Add weighted direct edges.
    static void addEdge(int from, int to, int cost){
        Edge e = new Edge(to, cost);
        graph[from].add(e);
    }

    static void shortestPathFasterAlgorithm(int s){
        dist = new int[n];
        pred = new int[n];
        onQueue = new boolean[n];
        Arrays.fill(dist, INF);
        Queue<Integer> queue = new LinkedList<>();
        queue.offer(s);
        dist[s] = 0;
        onQueue[s] = true;
        while (!queue.isEmpty()){
            int cur = queue.poll();
            onQueue[cur] = false;
            for (Edge e : graph[cur]){
                if (dist[cur] + e.cost < dist[e.to]){
                    dist[e.to] = dist[cur] + e.cost; // Edge Relaxation
                    pred[e.to] = cur; // store previous node
                    if (onQueue[e.to] == false){ // Node(e.to) is not in the queue
                        onQueue[e.to] = true;
                        queue.offer(e.to);
                    }
                }
            }
        }
    }

    static void printPathReconstruction(int start, int end){
        if (end == start) {
            System.out.print(start);
            return;
        }
        pathReconstruction(start, pred[end]);
        System.out.print(" -> " + end );
    }

    public static void main(String[] args) throws IOException {
        BufferedReader br = new BufferedReader(new InputStreamReader(System.in));

        n = 6;
        int start = 0;
        createGraph();
        addEdge(0, 1, 4);
        addEdge(0, 2, 2);
        addEdge(1, 2, 5);
        addEdge(1, 3, 10);
        addEdge(2, 4, 3);
        addEdge(3, 5, 11);
        addEdge(4, 3, 4);

        shortestPathFasterAlgorithm(start);

        System.out.println("Shortest path distance : " + dist[5]);
        System.out.print("Shortest path : ");
        printPathReconstruction(start, 5);
    }

    static class Edge{
        int to;
        int cost;

        public Edge(int to, int cost) {
            this.to = to;
            this.cost = cost;
        }
    }
}

Output:

Shortest path distance : 20
Shortest path : 0 -> 2 -> 4 -> 3 -> 5

Optimization techniques

Small Label First (SLF) technique.

변 경감(Edge relaxation) 되어진 정점 $v$를 항상 Queue 뒤에 추가하였지만 이 technique에서는 그 추가되어진 정점 $v$의 $d(v)$와 Queue의 맨 앞 정점의 거리 $d(front(Q))$를 비교하고 $d(v)$가 더 작다면 $d(v)$를 Queue의 맨 앞으로 보낸다. 이 technique은 front에 원소 추가를 요구하므로 front와 rear 전부 pop(), offer()연산을 지원하는 Deque(데크) 자료구조를 사용함으로써 구현할 수 있다.

위 SPFA 자바 메소드에서 Queue<Integer> queue = new LinkedList<>();를 Deque<Integer> queue = new LinkedList<>();로 하여 Deque를 사용한다.

다음은 이 technique의 의사코드이다.

procedure Small-Label-First(G, Q)
     if d(back(Q)) < d(front(Q)) then
         u := pop back of Q
         push u into front of Q

다음은 SPFA에 위 최적화를 적용한 코드이다.

static void shortestPathFasterAlgorithm(int s){
    dist = new int[n];
    pred = new int[n];
    onQueue = new boolean[n];
    Arrays.fill(dist, INF);
    Deque<Integer> queue = new LinkedList<>();
    queue.offer(s);
    dist[s] = 0;
    onQueue[s] = true;
    while (!queue.isEmpty()){
        int cur = queue.poll();
        onQueue[cur] = false;
        for (Edge e : graph[cur]){
            if (dist[cur] + e.cost < dist[e.to]){
                dist[e.to] = dist[cur] + e.cost; // Edge Relaxation
                pred[e.to] = cur; // store previous node
                if (onQueue[e.to] == false){ // Node(e.to) is not in the queue
                    onQueue[e.to] = true;
                    queue.offer(e.to);
                    // Optimization <Small Label First>
                    if (dist[e.to] < dist[queue.peekFirst()]){
                        queue.offerFirst(queue.pollLast());
                    }
                }
            }
        }
    }
}

Large Label Last (LLL) technique.

Queue의 front 원소의 값이 현재 Queue에 들어있는 모든 정점의 평균보다 작게 하기 위해, Queue에 들어있는 모드 정점 $v$의 평균을 구하고, Queue 앞에서 부터 평균보다 큰 값을 가진 정점 $v$들을 Queue의 맨 뒤로 보내는 연산이다. 평균보다 작은 값을 가진 정점 $v$가 나오면 loop를 빠져나온다.

다음은 이 technique의 의사코드이다.

 procedure Large-Label-Last(G, Q)
     x := average of d(v) for all v in Q
     while d(front(Q)) > x
         u := pop front of Q
         push u to back of Q

Running time

The worst-case running time : $O(|V|\cdot|E|)$

SPFA의 최악 실행 시간은 standard Bellman-Ford algorithm과 같은 $O(|V|\cdot|E|)$ 이다.

The average running time : $O(|E|)$

실험으로 보여지는 SPFA의 평균 실행 시간은 $O(|E|)$ 수준이다. 그러나 평균 실행 시간은 아직 증명 되지 않았다.

References

Share on

Twitter Facebook LinkedIn

SPFA(Shortest Path Faster Algorithm)

Gyeong

SPFA(Shortest Path Faster Algorithm)

Algorithm

Step by step

Implementation

Optimization techniques

Small Label First (SLF) technique.

Large Label Last (LLL) technique.

Running time

References

Share on

Leave a comment

You may also enjoy

Sequence to Sequence with Attention

Recurrent Neural Network, Types of RNNs and LSTM

Intro to NLP, Bag-of-Words, Naive Bayes Classifier

Sequential Models - RNN