깊이우선탐색 글 참고하기
그래프의 구현 글 참고하기
이번 글에서는 스택을 사용한 DFS를 이해하고 구현해 봅니다.
깊이우선탐색(Depth First Search, DFS)
깊이우선탐색(DFS)은 트리나 그래프 혹은 다른 구조 상에서 탐색을 위한 알고리즘이다. 이 알고리즘은 루트 노드를 시작으로(그래프의 경우에는 임의의 노드를 루트 노드로 정하게 된다.) 탐색을 하다가 더 이상 갈 수 없어 백트랙 하기 전까지 가능한 한 가지를 따라 깊게 멀리 탐색한다.
시간 및 공간 복잡도 분석은 많은 응용분야에 따라 다른데, 이론적인 컴퓨터 과학 분야에서 DFS는 전체 그래프를 탐색하는데 사용되기 때문에 수행 시간은 선형인 $O(|V|+|E| )$가 된다. 공간 복잡도면을 보면 스택을 사용한 DFS는 최악 $O(|E|)$의 복잡도를 가진다. 재귀적인 방법과는 달리, 해당 정점에서 방문하지 않은 인접 정점들의 정보를 모두 스택에 저장하기 때문에, 최악 $O(|E|)$가 된다. ($|V|$는 정점의 수, $|E|$는 간선의 수이다.)
알고리즘
우선, 방문할 인접 정점들을 저장할 Stack과 정점들의 방문 표시를 할 visited[] 배열을 선언한다.
스택을 이용한 DFS 알고리즘은 다음과 같은 순서로 실행된다.
-
탐색을 시작할 스타팅 노드를 스택에 넣는다.
-
스택이 빈 공간이 아닐 때 까지 다음을 실행한다.
-
스택에서 정점 하나를 꺼내 방문하지 않았으면 방문 표시를 하고 그 정점에 인접한 모든 정점을 스택에 넣는다.(방문 하지 않은 정점들만)
-
2번으로 간다.
예제
예를 들어 DFS 알고리즘을 이해 해보자.
방문 우선순위: 현재 정점과 인접한 정점이 여러개면 번호가 [작은 순서대로] 방문한다.
아래와 같은 정점 5개로 이루어진 비방향 그래프로 DFS를 시작한다.
탐색은 0번 정점부터 시작한다고 가정한다.
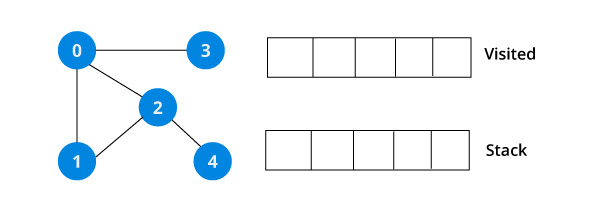
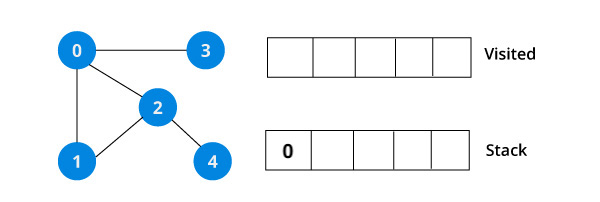
위 알고리즘에 따라 탐색을 시작할 0번 정점을 스택에 넣는다.
스택에서 가장 위에있는 원소를 하나 꺼낸다. (여기서는 제일 왼쪽 칸이 top이다.) 0번 정점을 방문표시 하고 0번 정점과 인접한 정점들 중에서 방문하지 않는 정점들을 모두 스택에 넣는다.
0번 정점과 1, 2, 3번 정점이 인접해 있다. 위의 방문 우선순위에 따라 인접한 정점이 여러개면 번호가 [작은 순서대로] 방문해야 하므로 3, 2, 1순으로 스택에 삽입한다. (후입 선출)
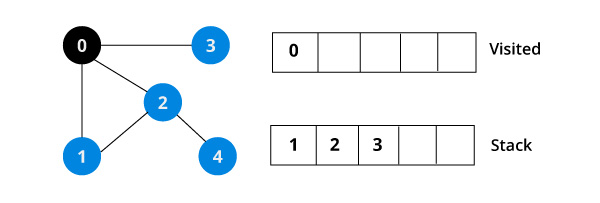
계속해서, 스택에서 가장 위에있는 1번 정점을 꺼낸다.
1번 정점을 방문표시 하고 1번 정점과 인접한 정점들 중에서 방문하지 않는 정점들을 모두 스택에 넣는다.
여기서는 2번 정점을 스택에 삽입한다.
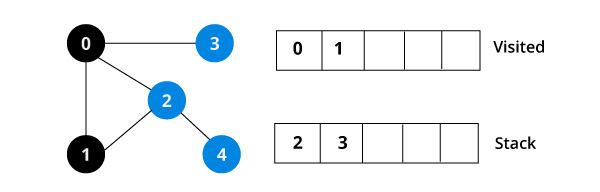
그 다음, 스택에서 가장 위에있는 2번 정점을 꺼낸다.
2번 정점을 방문표시 하고 2번 정점과 인접한 정점들 중에서 방문하지 않는 정점들을 모두 스택에 넣는다.
여기서는 4번 정점을 스택에 삽입한다.
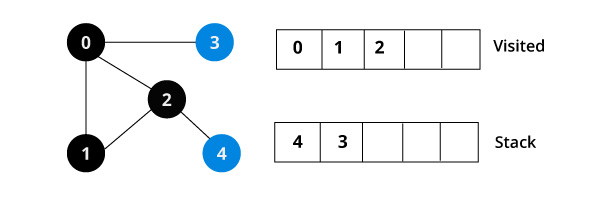
그 다음, 스택에서 가장 위에있는 4번 정점을 꺼낸다.
4번 정점을 방문표시 하고 4번 정점과 인접한 정점들 중에서 방문하지 않는 정점들을 모두 스택에 넣는다.
4번 정점과 인접한 정점 중에서는 방문하지 않은 정점들이 없으므로 다음 스탭으로 간다.
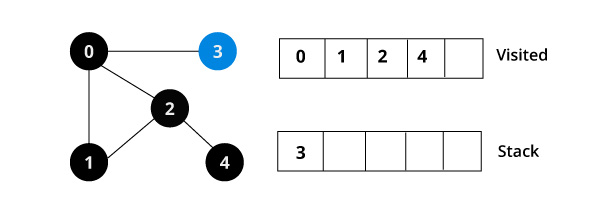
그 다음, 스택에서 가장 위에있는 3번 정점을 꺼낸다.
3번 정점을 방문표시 하고 3번 정점과 인접한 정점들 중에서 방문하지 않는 정점들을 모두 스택에 넣는다.
3번 정점과 인접한 정점 중에서는 방문하지 않은 정점들이 없으므로 다음 스탭으로 간다.
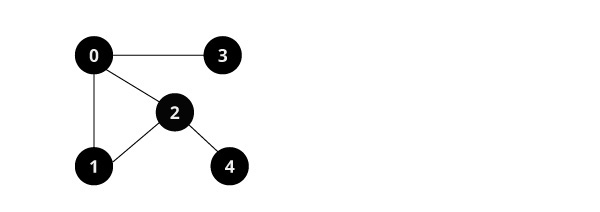
알고리즘 2번에 의해 스택이 모두 비었으니 알고리즘을 끝낸다.
스택을 이용한 DFS의 방문순서는 0 1 2 4 3 순이다.
구현
의사코드
스택을 이용한 반복적인 방법
Input: 그래프 G, 그래프 G의 정점 v
Output: v로 부터 탐색 가능한 모든 정점들
procedure DFS-iterative(G, v) is
let S be a stack
S.push(v)
while S is not empty do
v = S.pop()
if v is not labeled as discovered then
label v as discovered
for all edges from v to w in G.adjacentEdges(v) do
if w is not labeled as discovered then
S.push(w)
한 구문씩 보자.
let S be a stack:S라는 스택을 하나 생성한다. 현재 방문 정점의 인접 정점들을 담는다.S.push(v):탐색하고자 하는 시작 정점 v를 스택에 push한다.- while S is not empty do: 스택이 빈 공간이 아닐 때 까지 아래 연산들을 반복한다.
v = S.pop():현재 탐색 하고 있는 정점을 v에 넣는다.if v is not labeled as discovered then label v as discovered:만약 v가 탐색되지 않았으면, 탐색 완료 표시를 한다.for all edges from v to w in G.adjacentEdges(v) do if w is not labeled as discovered then S.push(w):현재 정점 v의 모든 인접한 정점 w를 스택에 넣는다. (w가 방문되지 않았으면)
자바 프로그램
위 의사코드를 바탕으로 스택을 이용한 DFS 알고리즘 자바 코드는 다음과 같다.
public void DFS(int start){
boolean[] visited = new boolean[vertex];
Stack<Integer> stack = new Stack<Integer>();
stack.push(start);
while (!stack.isEmpty()){
int v = stack.pop();
if (!visited[v]){
visited[v] = true;
for (int i = 0; i < list[v].size(); i++){
int dest = list[v].get(i);
if (!visited[dest])
stack.push(dest);
}
}
}
}
위의 코드 설명
boolean[] visited = new boolean[vertex];
Stack<Integer> stack = new Stack<Integer>();
방문할 인접 정점들을 저장할 Stack과 정점들의 방문 표시를 할 visited[] 배열을 선언한다.
stack.push(start);
탐색을 시작할 스타팅 노드를 스택에 넣는다.
while (!stack.isEmpty()){}
스택이 빈 공간이 아닐 때 까지 다음을 실행한다.
int v = stack.pop();
if (!visited[v]){
visited[v] = true;
for (int i = 0; i < list[v].size(); i++){
int dest = list[v].get(i);
if (!visited[dest])
stack.push(dest);
}
}
스택에서 정점 하나를 꺼내 방문하지 않았으면 방문 표시를 하고 그 정점에 인접한 모든 정점을 스택에 넣는다.(방문 하지 않은 정점들만)
위의 예제 그래프를 사용한 전체 코드는 다음과 같다.
DFSIterative.java
import java.util.LinkedList;
import java.util.Stack;
public class DFSIterative {
static class Graph{
int vertex;
LinkedList<Integer> list[];
public Graph(int vertex) {
this.vertex = vertex;
list = new LinkedList[vertex];
for (int i = 0; i <vertex ; i++) {
list[i] = new LinkedList<>();
}
}
public void addEdge(int source, int destination){
list[source].addFirst(destination);
list[destination].addFirst(source);
}
public void DFS(int start){
System.out.print("Depth First Traversal: ");
boolean[] visited = new boolean[vertex];
Stack<Integer> stack = new Stack<Integer>();
stack.push(start);
while (!stack.isEmpty()){
int v = stack.pop();
if (!visited[v]){
System.out.print(v + " ");
visited[v] = true;
for (int i = 0; i < list[v].size(); i++){
int dest = list[v].get(i);
if (!visited[dest])
stack.push(dest);
}
}
}
}
public void printGraph(){
for (int i = 0; i <vertex ; i++) {
LinkedList<Integer> nodeList = list[i];
if(nodeList.isEmpty()==false) {
System.out.print("source = " + i + " is connected to nodes: ");
for (int j = 0; j < nodeList.size(); j++) {
System.out.print(" " + nodeList.get(j));
}
}
System.out.println();
}
}
}
public static void main(String[] args) {
Graph graph = new Graph(6);
graph.addEdge(0, 1);
graph.addEdge(0, 2);
graph.addEdge(1, 2);
graph.addEdge(1, 3);
graph.addEdge(3, 4);
graph.addEdge(2, 3);
graph.addEdge(4, 0);
graph.addEdge(4, 1);
graph.addEdge(4, 5);
graph.printGraph();
graph.DFS(0);
}
}
Output:
source = 0 is connected to nodes: 3 2 1
source = 1 is connected to nodes: 2 0
source = 2 is connected to nodes: 4 1 0
source = 3 is connected to nodes: 0
source = 4 is connected to nodes: 2
Depth First Traversal: 0 1 2 4 3
Process finished with exit code 0

Leave a comment