깊이우선탐색 글 참고하기
그래프의 구현 글 참고하기
이번 글에서는 재귀 함수를 사용한 DFS를 이해하고 구현해 봅니다.
깊이우선탐색(Depth First Search, DFS)
깊이우선탐색(DFS)은 트리나 그래프 혹은 다른 구조 상에서 탐색을 위한 알고리즘이다. 이 알고리즘은 루트 노드를 시작으로(그래프의 경우에는 임의의 노드를 루트 노드로 정하게 된다.) 탐색을 하다가 더 이상 갈 수 없어 백트랙 하기 전까지 가능한 한 가지를 따라 깊게 멀리 탐색한다.
시간 및 공간 복잡도 분석은 많은 응용분야에 따라 다른데, 이론적인 컴퓨터 과학 분야에서 DFS는 전체 그래프를 탐색하는데 사용되기 때문에 수행 시간은 선형인 $O(|V|+|E| )$가 된다. 공간 복잡도면을 보면 DFS는 경로상의 현재 탐색하고 있는 정점과 경로상 이미 방문한 정점들의 콜 스택 정보를 저장하고 있기 때문에 최악 $O(|V|)$의 공간을 요구한다. ($|V|$는 정점의 수, $|E|$는 간선의 수이다.)
알고리즘
재귀 함수를 이용한 DFS 알고리즘은 다음과 같은 순서로 실행된다.
-
탐색을 시작할 스타팅 노드를 매개변수로 하여 DFS 함수를 실행한다.
-
현재 탐색 정점을 방문 표시한다.
-
현재 정점에 인접한 모든 정점 중에서 방문하지 않은 정점을 재귀적으로 탐색한다.
현재 정점에 인접한 모든 정점을 방문 하였으면 이전 정점으로 백트래킹 한다. -
2번으로 간다.
예제
예를 들어 DFS 알고리즘을 이해 해보자.
방문 우선순위: 현재 정점과 인접한 정점이 여러개면 번호가 [작은 순서대로] 방문한다.
아래와 같은 정점 5개로 이루어진 비방향 그래프 G로 DFS를 시작한다.
DFS(G, 정점 번호)는 그래프 G와 정점 번호를 매개변수로 하여 DFS함수를 재귀적으로 호출하는 것을 의미한다.
탐색은 0번 정점부터 시작한다고 가정한다.
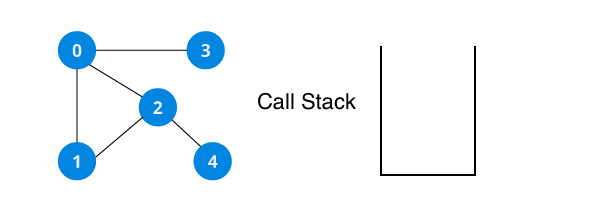
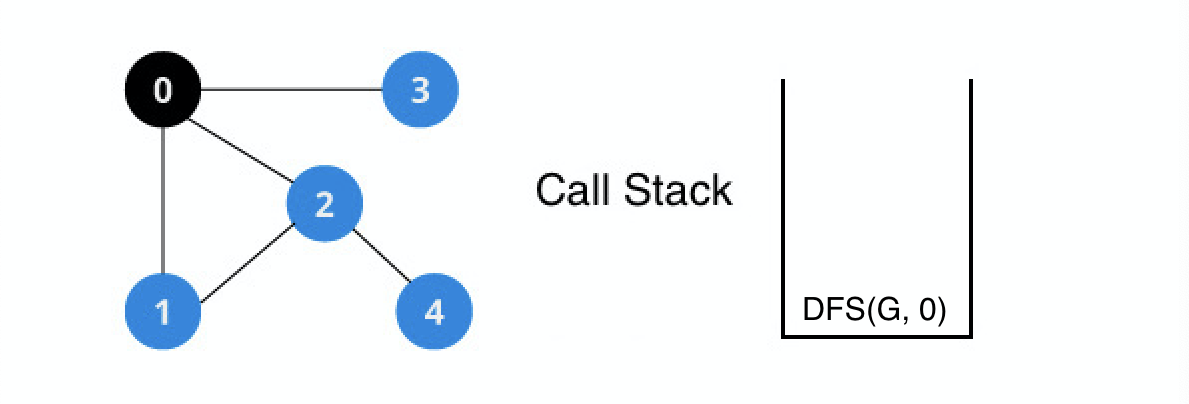
DFS(G, 0) 실행
0번 정점을 방문한다.
0번 정점의 인접 정점들 중 탐색하지 않은 정점들을 탐색한다.
1번 정점을 재귀적으로 탐색한다.
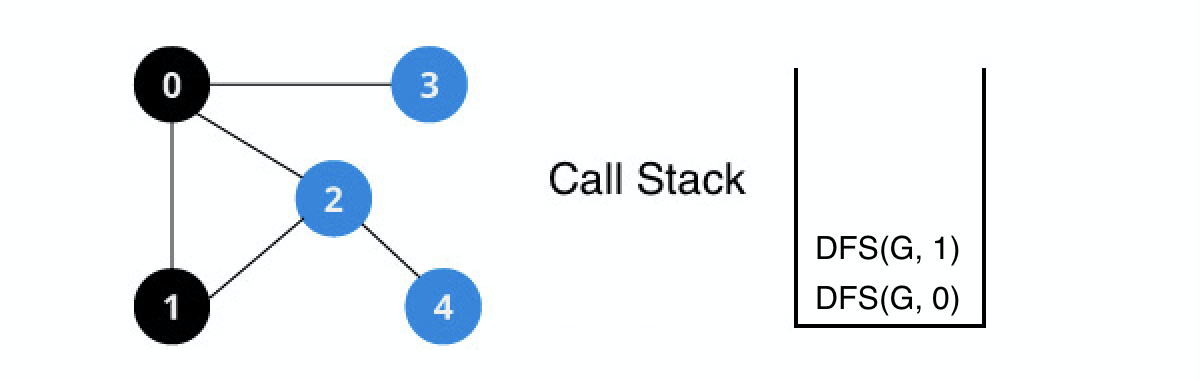
DFS(G, 1) 실행
1번 정점을 방문한다.
1번 정점의 인접 정점들 중 탐색하지 않은 정점들을 탐색한다.
2번 정점을 재귀적으로 탐색한다.
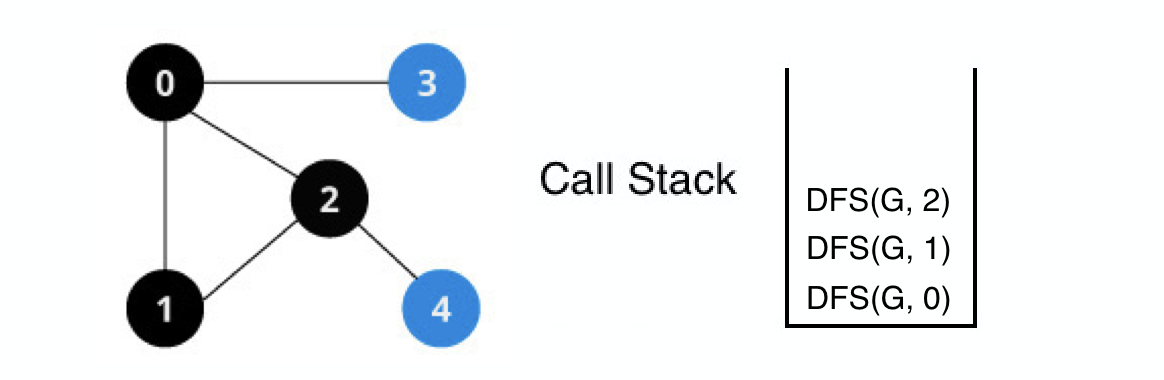
DFS(G, 2) 실행
2번 정점을 방문한다.
2번 정점의 인접 정점들 중 탐색하지 않은 정점들을 탐색한다.
4번 정점을 재귀적으로 탐색한다.
DFS(G, 4) 실행
4번 정점을 방문한다.
4번 정점의 인접 정점들 중 탐색하지 않은 정점들을 탐색한다.
인접 정점들 중 방문 하지 않은 정점이 없으므로 이전 정점으로 백트랙 한다.
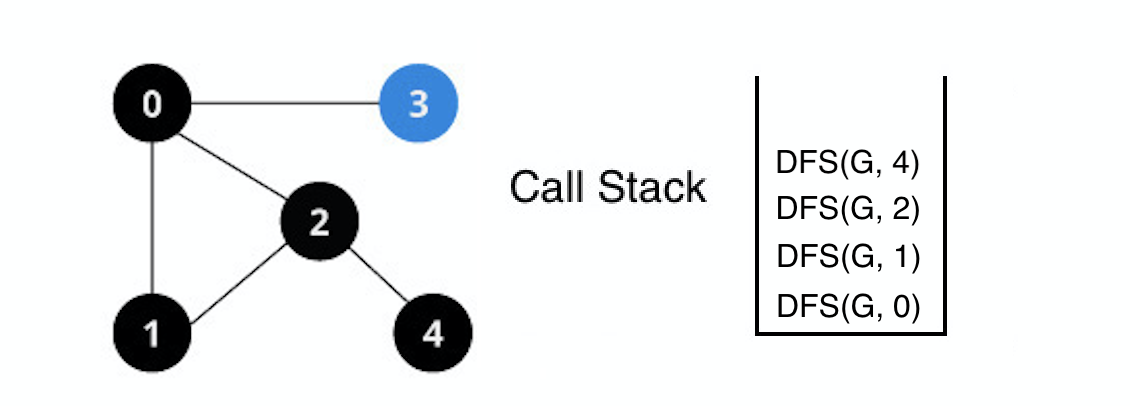
DFS(G, 2) 백트랙
2번 정점의 인접 정점들 중 탐색하지 않은 정점들을 탐색한다.
인접 정점들 중 방문 하지 않은 정점이 없으므로 이전 정점으로 백트랙 한다.
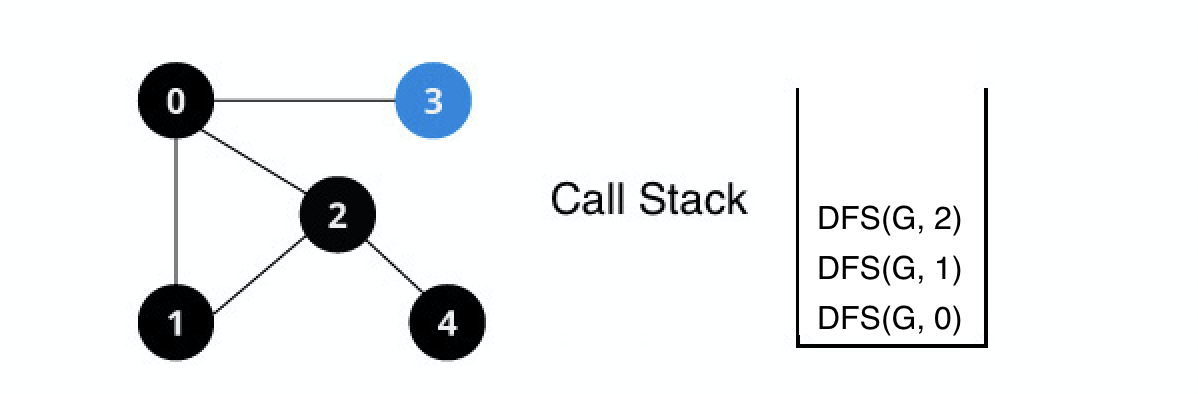
DFS(G, 1) 백트랙
1번 정점의 인접 정점들 중 탐색하지 않은 정점들을 탐색한다.
인접 정점들 중 방문 하지 않은 정점이 없으므로 이전 정점으로 백트랙 한다.
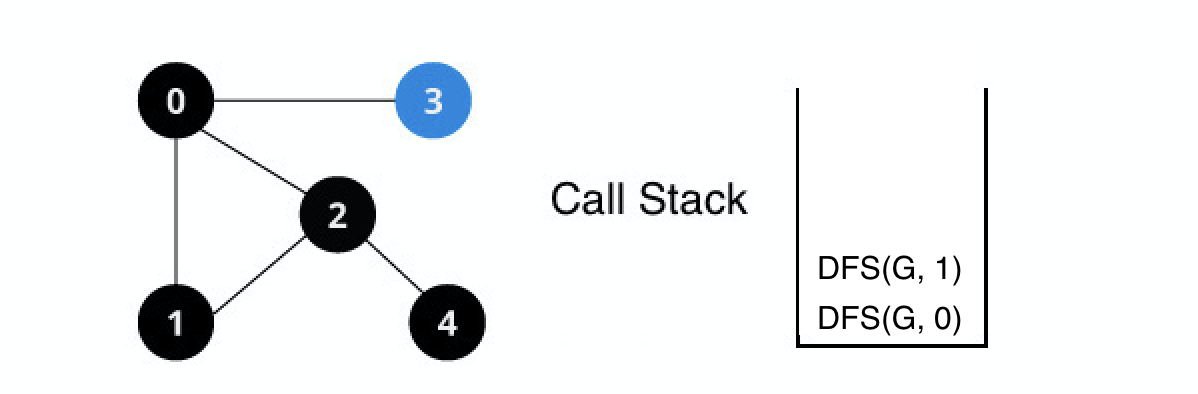
DFS(G, 0) 백트랙
0번 정점의 인접 정점들 중 탐색하지 않은 정점들을 탐색한다.
3번 정점을 재귀적으로 탐색한다.
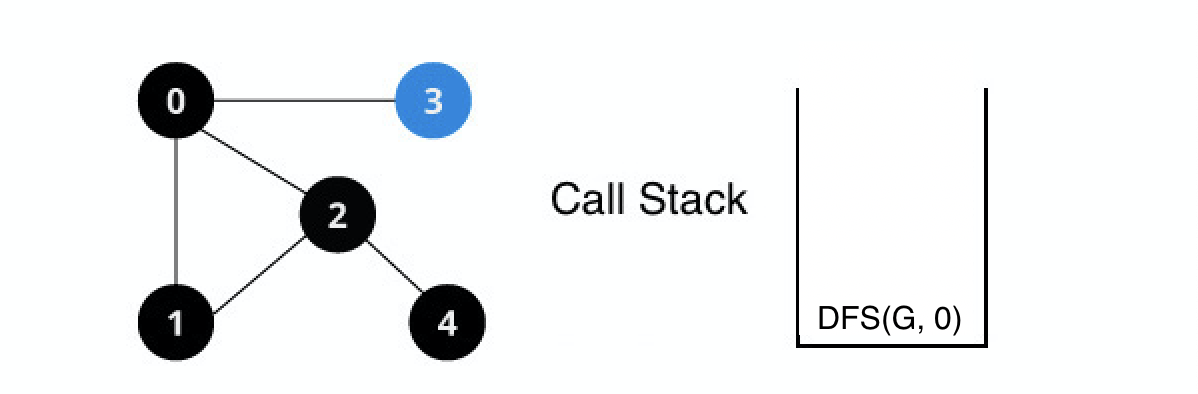
DFS(G, 3) 실행
3번 정점을 방문한다.
3번 정점의 인접 정점들 중 탐색하지 않은 정점들을 탐색한다.
인접 정점들 중 방문 하지 않은 정점이 없으므로 이전 정점으로 백트랙 한다.
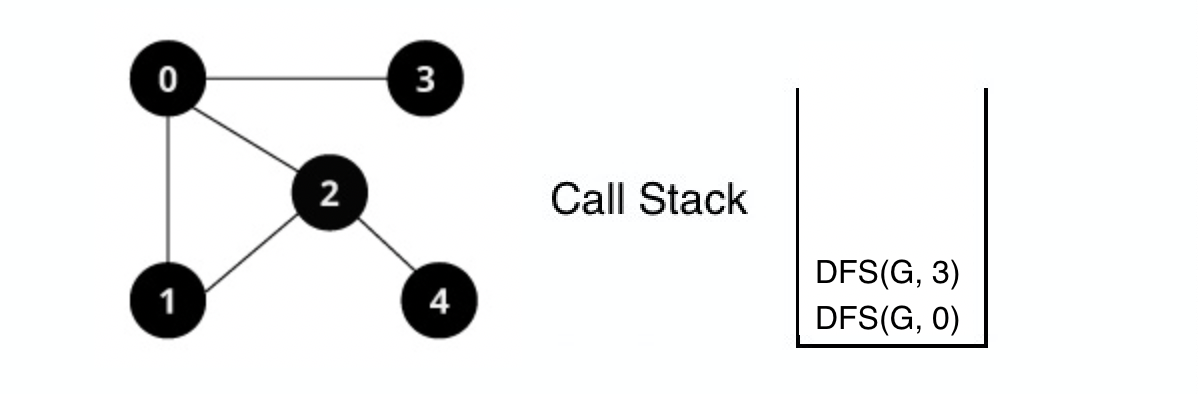
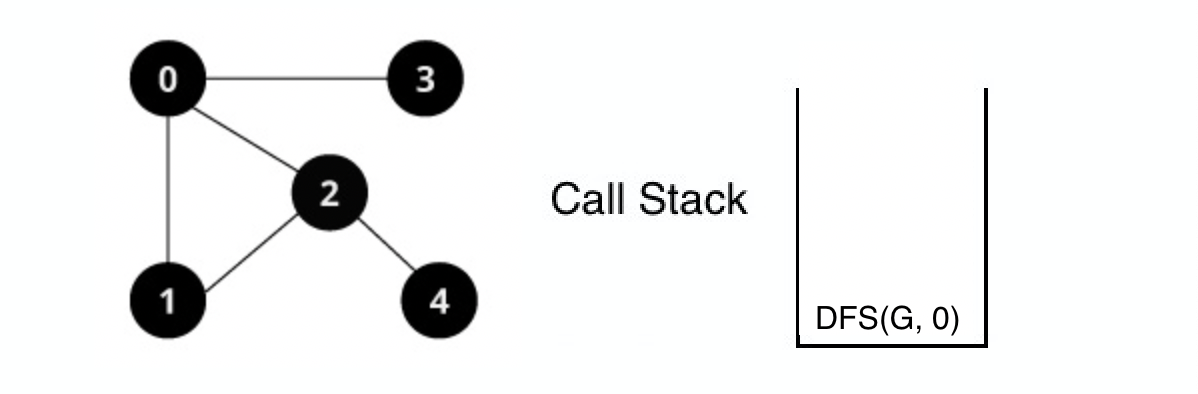
DFS(G, 0) 백트랙
1번 정점의 인접 정점들 중 탐색하지 않은 정점들을 탐색한다.
인접 정점들 중 방문 하지 않은 정점이 없으므로 DFS(G, 0)이 콜 스택에서 사라진다.
콜스택이 비었으므로 알고리즘을 끝낸다.
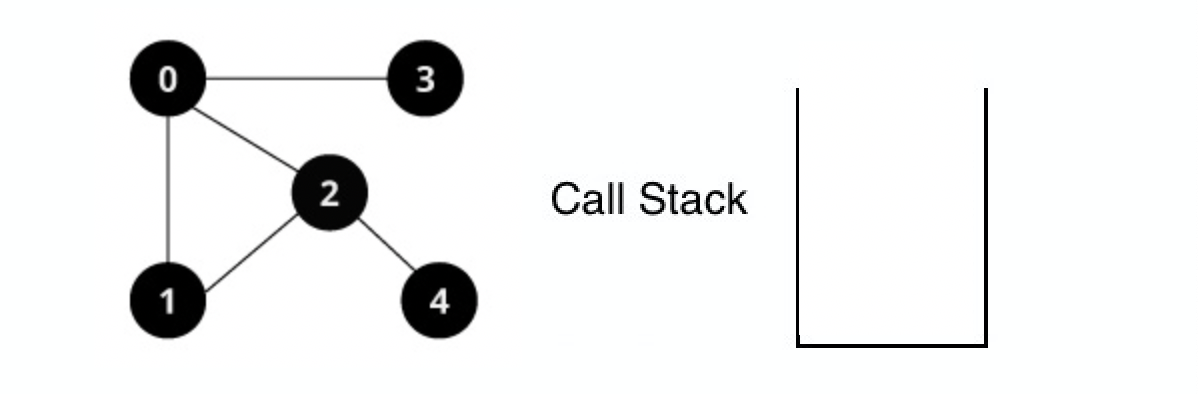
재귀 함수를 이용한 DFS의 방문순서는 0 1 2 4 3 순이다.
구현
의사코드
다음은 서브루틴을 이용한 재귀적 방법의 의사코드이다.
Input: 그래프 G, 그래프 G의 정점 v
Output: v로 부터 탐색 가능한 모든 정점들
procedure DFS(G, v) is
label v as discovered
for all directed edges from v to w that are in G.adjacentEdges(v) do
if vertex w is not labeled as discovered then
recursively call DFS(G, w)
한 구문씩 보자.
label v as discovered: 현재 정점 v를 탐색완료 되었다는 것을 표시한다. (중복 방문 방지를 위해)for all directed edges from v to w that are in G.adjacentEdges(v) do: 그래프 G의 모든 인접한 간선 (v, w)에 대해서if vertex w is not labeled as discovered then: 만약 w가 탐색되지 않았으면recursively call DFS(G, w): 재귀적으로 w를 탐색한다.
이것은 현재 정점 v의 인접 정점 w를 매개변수로 하여 같은 서브루틴으로 다음 정점을 탐색하는 것을 의미한다.
자바 프로그램
위 의사코드를 바탕으로 재귀 함수를 이용한 DFS 알고리즘 자바 코드는 다음과 같다.
public void DFSRecursion(int startVertex){
boolean [] visited = new boolean[vertices];
dfs(startVertex, visited);
}
public void dfs(int start, boolean [] visited){
visited[start] = true;
for (int i = 0; i <adjList[start].size() ; i++) {
int destination = adjList[start].get(i);
if(!visited[destination])
dfs(destination,visited);
}
}
위의 코드 설명
public void DFSRecursion(int startVertex){
boolean [] visited = new boolean[vertices];
dfs(startVertex, visited);
}
정점들의 방문 표시를 할 visited[] 배열을 선언한다. 그 다음 탐색 시작 정점과, visited[] 배열을 매개변수로 하는 dfs 함수를 시작한다.
visited[start] = true;
현재 탐색 중인 정점을 방문 표시한다.
for (int i = 0; i <adjList[start].size() ; i++) {}
현재 탐색 중인 인접 정점들에 대하여
int destination = adjList[start].get(i);
if(!visited[destination])
dfs(destination,visited);
현재 탐색 중인 인접 정점 destination이 방문되지 않은 정점이면 destination을 다음 정점으로 하는 dfs 함수를 실행하여 재귀적으로 탐색한다.
위의 예제 그래프를 사용한 전체 코드는 다음과 같다.
DFSRecursion.java
import java.util.LinkedList;
public class DFSRecursion {
static class Graph{
int vertices;
LinkedList<Integer>[] adjList;
Graph(int vertices){
this.vertices = vertices;
adjList = new LinkedList[vertices];
for (int i = 0; i <vertices ; i++) {
adjList[i] = new LinkedList<>();
}
}
public void addEgde(int source, int destination){
adjList[source].add(destination);
adjList[destination].add(source);
}
public void DFSRecursion(int startVertex){
boolean [] visited = new boolean[vertices];
dfs(startVertex, visited);
}
public void dfs(int start, boolean [] visited){
visited[start] = true;
System.out.print(start + " ");
for (int i = 0; i <adjList[start].size() ; i++) {
int destination = adjList[start].get(i);
if(!visited[destination])
dfs(destination,visited);
}
}
}
public static void main(String[] args) {
int vertices = 6;
Graph graph = new Graph(vertices);
graph.addEgde(0, 1);
graph.addEgde(0, 2);
graph.addEgde(0, 3);
graph.addEgde(1, 2);
graph.addEgde(2, 4);
graph.DFSRecursion(0);
}
}
Output:
0 1 2 4 3

Leave a comment