깊이우선탐색(Depth First Search, DFS)
깊이우선탐색(DFS)은 트리나 그래프 혹은 다른 구조 상에서 탐색을 위한 알고리즘이다. 이 알고리즘은 루트 노드를 시작으로(그래프의 경우에는 임의의 노드를 루트 노드로 정하게 된다.) 탐색을 하다가 더 이상 갈 수 없어 백트랙 하기 전까지 가능한 한 가지를 따라 깊게 멀리 탐색한다.
시간 및 공간 복잡도 분석은 많은 응용분야에 따라 다른데, 이론적인 컴퓨터 과학 분야에서 DFS는 전체 그래프를 탐색하는데 사용되기 때문에 수행 시간은 선형인 $O(|V|+|E| )$가 된다. 공간 복잡도면을 보면 DFS는 경로상의 현재 탐색하고 있는 정점과 경로상 이미 방문한 정점들의 스택을 저장하고 있기 때문에 최악 $O(|V|)$의 공간을 요구한다. ($|V|$는 정점의 수, $|E|$는 간선의 수이다.)
깊이우선탐색(DFS)의 시간 및 공간 상한은 너비우선탐색(BFS)과 같기 때문에, 탐색 알고리즘의 사용면에서 두 알고리즘이 만드는 정점 방문 순서의 다름과 그 복잡성을 생각해 어느 알고리즘을 사용해야 할지 생각해야한다.
예제
다음 그래프를 보고 깊이우선탐색이 어떤 것인지 이해해보자.
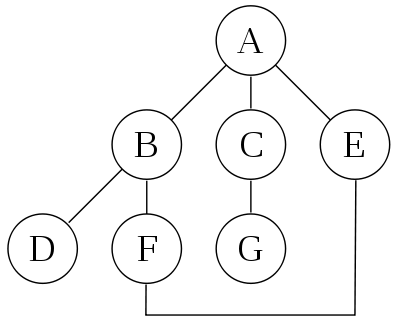
가정
- 현재 방문하고 있는 정점에서 인접한 왼쪽 간선을 오른쪽 간선보다 먼저 선택한다고 가정한다.
- 탐색 알고리즘은 현재 정점의 이전 정점의 방문을 기억한다고 가정한다.
- 정점들의 방문은 중복되지 않는다고 가정한다.
먼저 A를 루트 노드로 하여 탐색을 시작한다.
-
A를 방문하고 위의 가정에 따라 인접 정점 C, E를 탐색하기 전에 B를 먼저 탐색한다.
-
B를 방문하고 F를 탐색하기 전에 D를 먼저 탐색한다.
-
D를 방문하고 D의 인접한 정점은 B이지만 이미 방문하였기에 더 이상 탐색할 곳이 없으므로, 이전 정점 B로 백트래킹 한다.
-
정점 B에서 F를 탐색한다.
-
F를 방문하고 아직 탐색하지 않은 인접 정점인 E를 탐색한다.
-
E를 방문하고 나면 인접 정점들은 모두 방문한 상태이므로 이전 정점 F로 백트래킹 한다.
-
F에서도 인접 정점들은 모두 방문한 상태이므로 이전 정점 B로 백트래킹 한다.
-
B에서도 인접 정점들은 모두 방문한 상태이므로 이전 정점 A로 백트래킹 한다.
-
A에서 인접한 정점 중 아직 탐색하지 않은 곳은 C이므로 C를 탐색한다.
-
C를 방문하고 아직 탐색하지 않은 곳인 G를 탐색한다.
-
G를 방문한다.
-
G에서 인접 정점들은 모두 방문한 상태이므로 이전 정점 C로 백트래킹 한다.
-
C에서 인접 정점들은 모두 방문한 상태이므로 이전 정점 A로 백트래킹 한다.
-
A에서 모든 인접 정점이 방문 완료 되었으므로 DFS는 완료되었다.
이로서, DFS에 의한 위 그래프의 정점들 방문 순서는 : A, B, D, F, E, C, G 이다.
의사코드
깊이우선탐색(DFS)을 하는 두가지 방법을 알아본다.
서브루틴을 이용한 재귀적 방법
Input: 그래프 G, 그래프 G의 정점 v
Output: v로 부터 탐색 가능한 모든 정점들
다음은 서브루틴을 이용한 재귀적 방법의 의사코드이다.
procedure DFS(G, v) is
label v as discovered
for all directed edges from v to w that are in G.adjacentEdges(v) do
if vertex w is not labeled as discovered then
recursively call DFS(G, w)
한 구문씩 보자.
label v as discovered: 현재 정점 v를 탐색완료 되었다는 것을 표시한다. (중복 방문 방지를 위해)for all directed edges from v to w that are in G.adjacentEdges(v) do: 그래프 G의 모든 인접한 간선 (v, w)에 대해서if vertex w is not labeled as discovered then: 만약 w가 탐색되지 않았으면recursively call DFS(G, w): 재귀적으로 w를 탐색한다.
이것은 현재 정점 v의 인접 정점 w를 매개변수로 하여 같은 서브루틴으로 다음 정점을 탐색하는 것을 의미한다.
이 방법의 최악 공간 복잡도는 $O(|V|)$가 된다.
현재 탐색하고 있는 경로의 정점들과 이미 방문한 정점들의 스택을 저장하고 있기 때문이다.
스택을 이용한 반복적인 방법
Input: 그래프 G, 그래프 G의 정점 v
Output: v로 부터 탐색 가능한 모든 정점들
다음은 스택을 이용한 반복적인 방법의 의사코드이다.
procedure DFS-iterative(G, v) is
let S be a stack
S.push(v)
while S is not empty do
v = S.pop()
if v is not labeled as discovered then
label v as discovered
for all edges from v to w in G.adjacentEdges(v) do
S.push(w)
한 구문씩 보자.
let S be a stack: S라는 스택을 하나 생성한다. 현재 방문 정점의 인접 정점들을 담는다.S.push(v): 탐색하고자 하는 시작 정점 v를 스택에 push한다.- while S is not empty do: 스택이 빈 공간이 아닐 때 까지 아래 연산들을 반복한다.
v = S.pop(): 현재 탐색 하고 있는 정점을 v에 넣는다. if v is not labeled as discovered then label v as discovered: 만약 v가 탐색되지 않았으면, 탐색 완료 표시를 한다.for all edges from v to w in G.adjacentEdges(v) do S.push(w): 현재 정점 v의 모든 인접한 정점 w를 스택에 넣는다.
이 방법의 최악 공간 복잡도는 $O(|E|)$가 된다.
재귀적인 방법과는 달리, 어떤 해당 정점에서 인접 정점들의 정보를 모두 스택에 저장하기 때문에, 최악의 설정으로 하나의 정점이 다른 모든 정점과 직접 연결되어 있다면 공간 복잡도는 $O(|E|)$가 된다.
두 가지 접근의 차이점
위에서 살펴본 두 가지 DFS의 탐색 방법은 각 정점들의 이웃방문 순서가 서로 반대인데, 재귀적인 방법에서는 인접리스트 방식에서 정점 v의 첫번째 이웃을 먼저 방문하는 반면, 스택을 이용한 반복적인 방법에서는 정점 v의 이웃들이 스택에 역순으로 저장되기 때문에 인접 리스트 관점에서 정점 v의 첫번째 이웃은 제일 마지막(first in last out)에 탐색이 된다.
위 그래프를 예로 들면 재귀적인 방법으로의 방문 순서는 A, B, D, F, E, C, G가 되고, 스택을 이용한 반복적 접근에서는 A, E, F, B, D, C, G가 된다.
응용
DFS 탐색 알고리즘은 많은 곳에서 쓰이는데 예는 다음과 같다.
- 미로 찾기
- 그래프의 위상 정렬
- 모든 경우 다 해보기(전체 탐색)
- 연결 구성 요소 찾기
- 이분 그래프
링크
프로그래밍 언어로의 구현은 다음 글을 참고하면 좋다.
시간 복잡도 & 공간 복잡도
- 시간 복잡도: 최악 $O(|V|+|E| )$ (중복 방문 제외)
- 공간 복잡도: 최악 $O(|V|)$ (알고리즘이 재귀적 일 때)

Leave a comment