너비우선탐색(Breadth First Search, BFS)

너비우선탐색(Breadth First Search)

너비우선탐색(BFS)은 트리나 그래프 혹은 다른 구조 상에서 탐색을 위한 알고리즘이다. 이 알고리즘은 루트 노드를 시작으로(그래프의 경우에는 임의의 노드를 루트 노드로 정하게 된다.) 다음 레벨로 가기전에 현재 레벨에서 인접한 모든 이웃노드들을 탐색한다.

더 이상 탐색할 노드가 없어 백트랙 하기 전까지 가지를 따라 가능한 한 깊이 탐색하는 깊이우선탐색과는 다르게 너비우선탐색은 해당 정점에서 인접한 정점들을 모두 방문하는 레벨 탐색 즉, 깊이보다는 넓게 탐색하는 전략을 쓴다. 이를 위해 너비우선탐색은 큐(Queue) 자료구조를 이용하여 탐색 방법을 구성하게 된다.

시간 및 공간 복잡도 분석은 많은 응용분야에 따라 다른데, 이론적인 컴퓨터 과학 분야에서 BFS는 전체 그래프를 탐색하는데 사용되기 때문에 수행 시간은 선형인 $O(|V|+|E| )$가 된다. 공간 복잡도면을 보면 BFS는 어떤 해당 정점에서 인접 정점들의 정보를 모두 큐에 저장하기 때문에, 최악의 설정으로 하나의 정점이 다른 모든 정점과 직접 연결되어 있다면 최악 $O(|V|)$의 공간을 요구한다. ($|V|$는 정점의 수, $|E|$는 간선의 수이다.)

너비우선탐색(BFS)의 시간 및 공간 상한은 깊이우선탐색(BFS)과 같기 때문에, 탐색 알고리즘의 사용면에서 두 알고리즘이 만드는 정점 방문 순서의 다름과 그 복잡성을 생각해 어느 알고리즘을 사용해야 할지 생각해야한다.

예제

다음 트리를 보고 너비우선탐색이 어떤 것인지 이해해보자.

위에서 보이는 트리에서 정점들의 번호는 너비우선탐색을 적용한 뒤 정점들의 방문 순서와 같다.

1번 정점을 루트로 하여 탐색을 시작하면, 1번 정점을 방문하고 그 인접한 정점 2, 3, 4를 순서대로 방문한다. 그 다음 레벨의 5, 6, 7, 8을 순서대로 방문하고 그 다음 레벨 9, 10, 11, 12순으로 방문하게 된다.

너비우선탐색이 어떻게 동작하는지 알아보자.

가정

• 현재 방문하고 있는 정점에서 인접한 왼쪽 간선을 오른쪽 간선보다 먼저 선택한다.
• 정점들의 방문 순서를 위해 큐 자료구조를 사용한다.
• 정점들의 방문은 중복되지 않는다.
• 1번 정점 부터 탐색을 시작한다.

---

먼저 1번 정점을 루트로 하여 BFS 탐색을 시작한다.

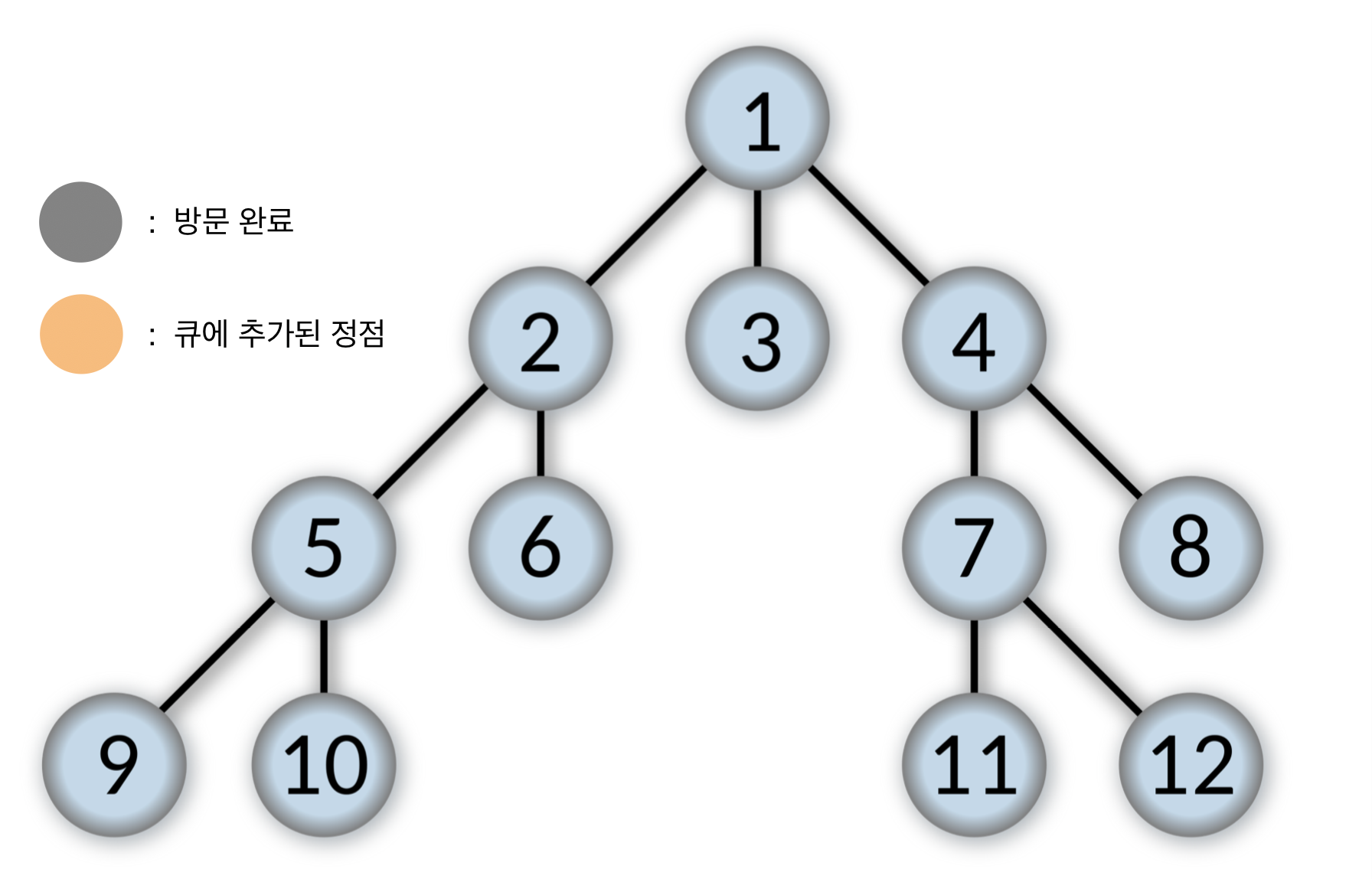
• 1번 정점을 큐에 넣는다.
  Queue: [1]

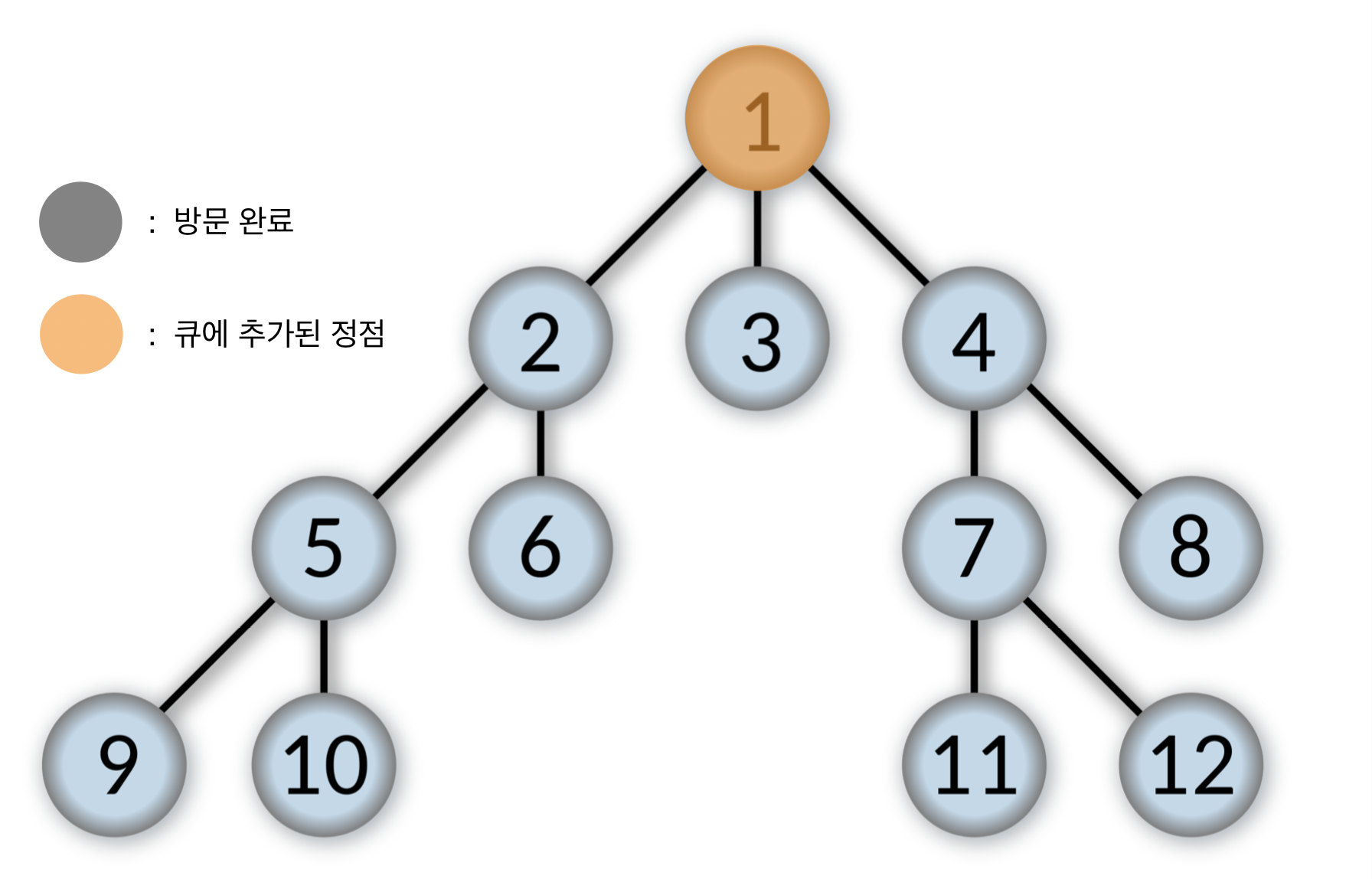
• 큐에서 제일 앞에 있는 1번을 pop하고, 1번 정점을 방문한다.
  1번 정점과 인접한 정점 중에서 방문하지 않은 2, 3, 4번을 순서대로 큐에 넣는다.
  Queue: [2, 3, 4]

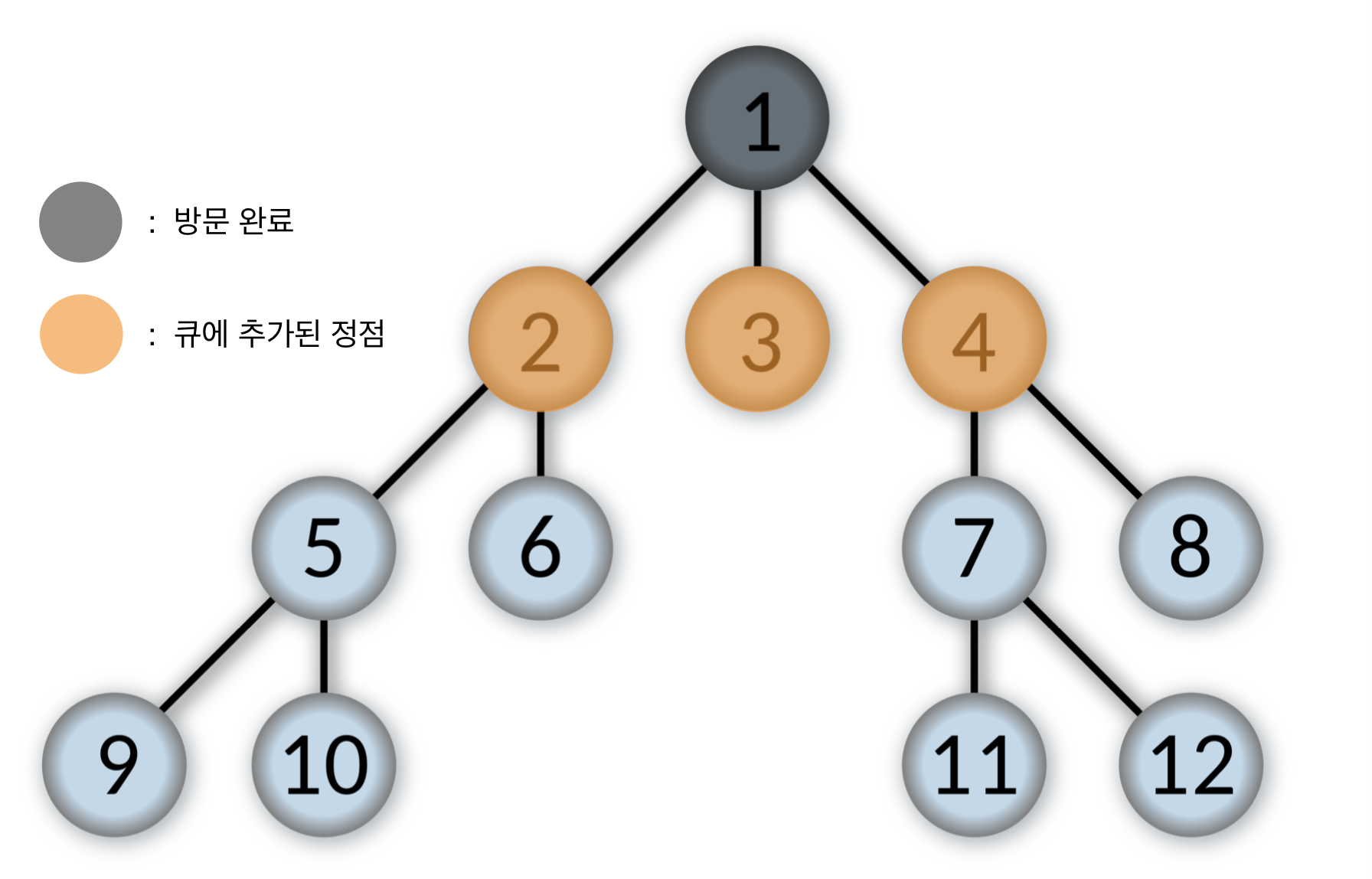
• 큐에서 제일 앞에 있는 2번을 pop하고, 2번 정점을 방문한다.
  2번 정점과 인접한 정점 중에서 방문하지 않은 5, 6번을 순서대로 큐에 넣는다.
  Queue: [3, 4, 5, 6]

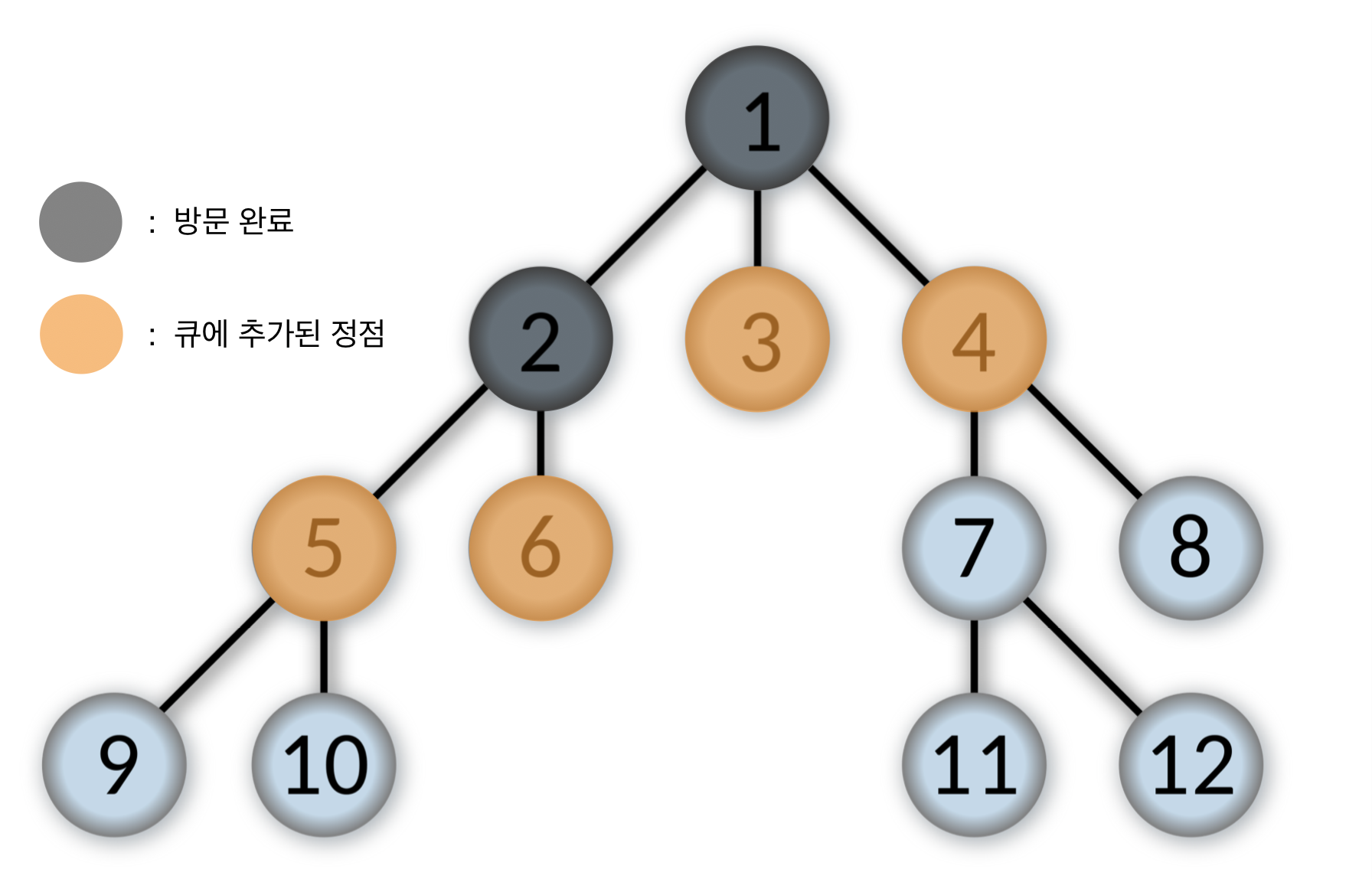
• 큐에서 제일 앞에 있는 3번을 pop하고, 3번 정점을 방문한다.
  3번 정점과 인접한 정점 중에서 방문하지 않은 정점이 없으므로 다음 스탭으로 간다.
  Queue: [4, 5, 6]

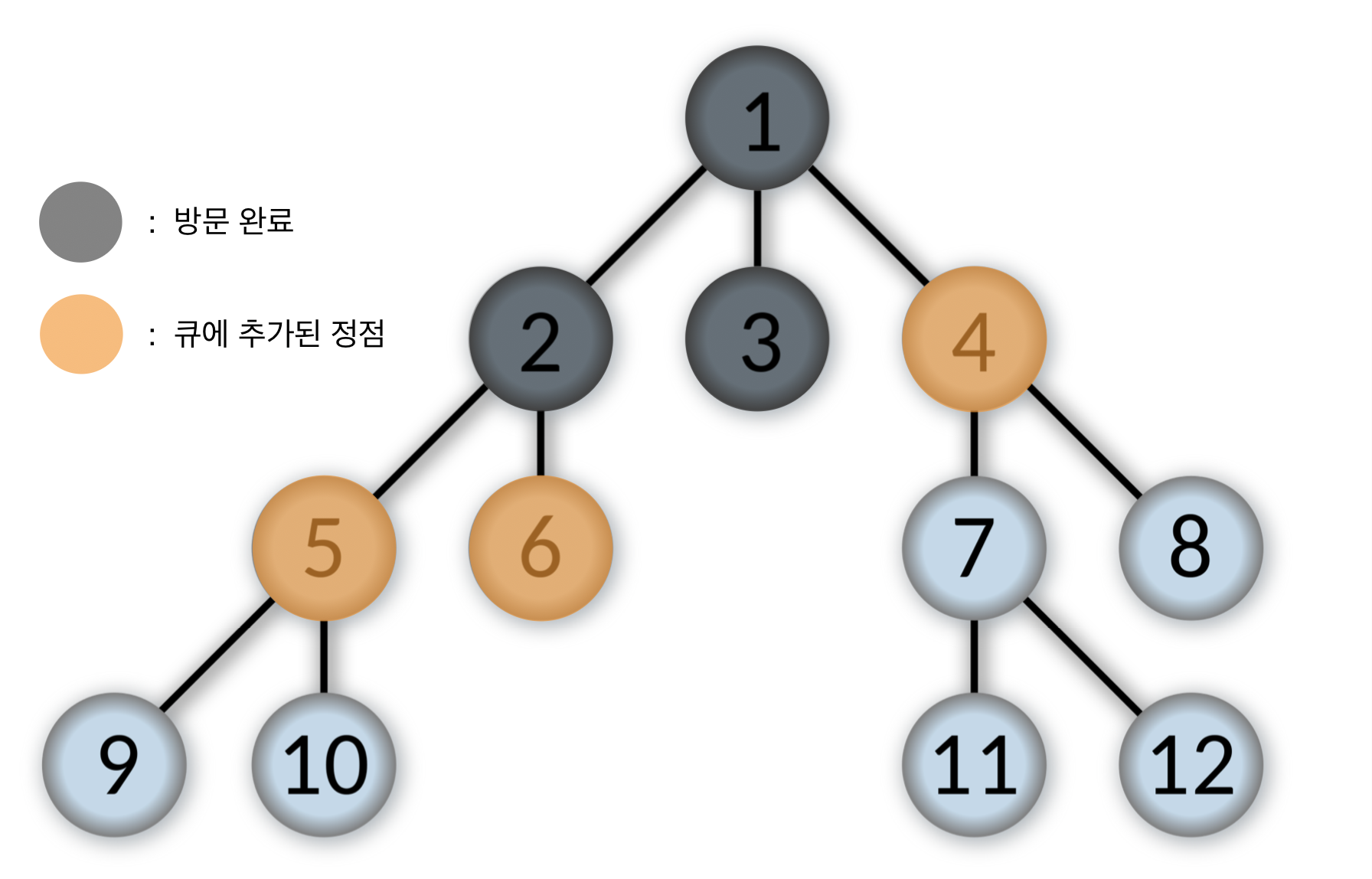
• 큐에서 제일 앞에 있는 4번을 pop하고, 4번 정점을 방문한다.
  4번 정점과 인접한 정점 중에서 방문하지 않은 7, 8번을 순서대로 큐에 넣는다.
  Queue: [5, 6, 7, 8]

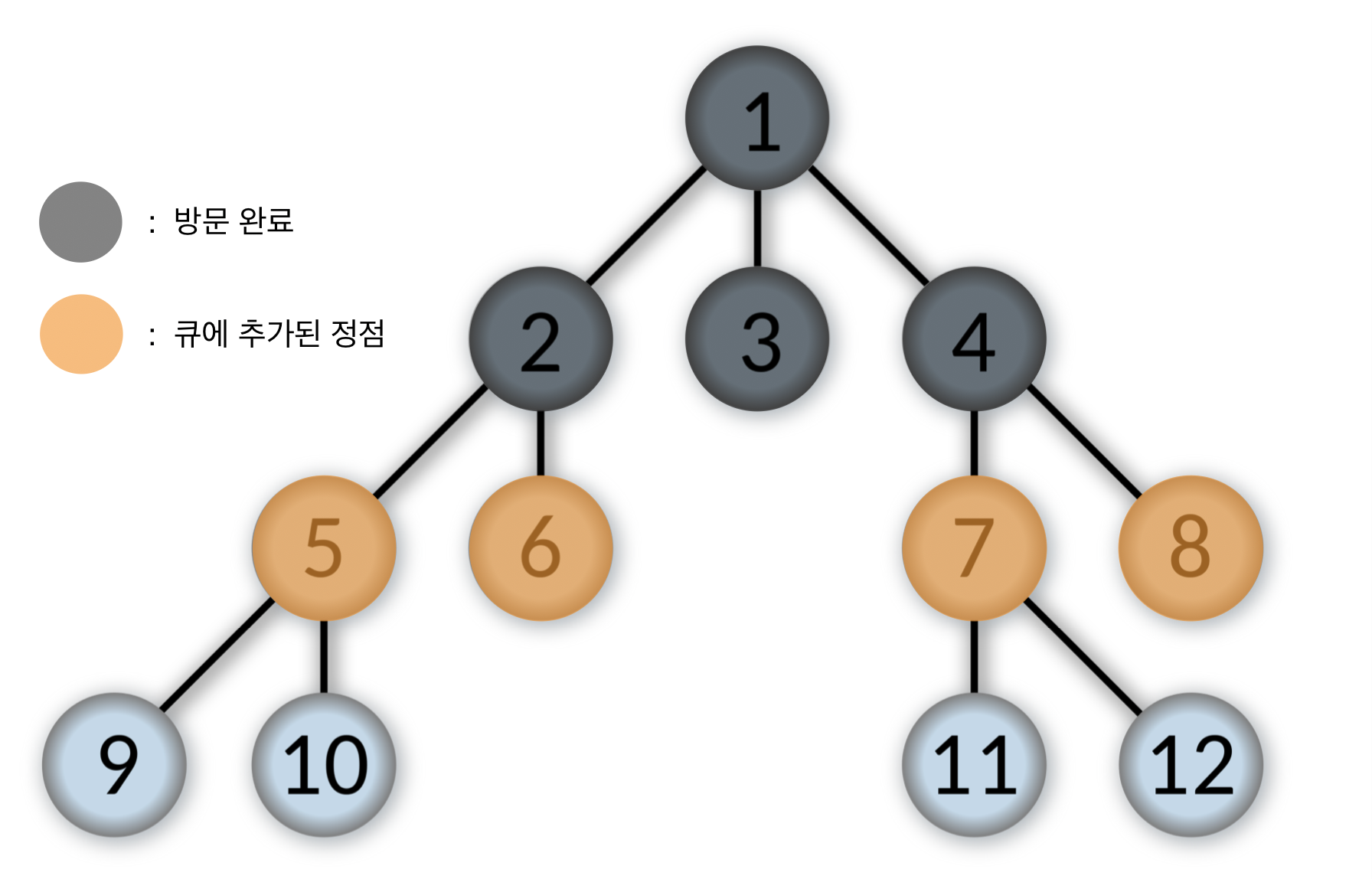
• 큐에서 제일 앞에 있는 5번을 pop하고, 5번 정점을 방문한다.
  5번 정점과 인접한 정점 중에서 방문하지 않은 9, 10번을 순서대로 큐에 넣는다.
  Queue: [6, 7, 8, 9, 10]

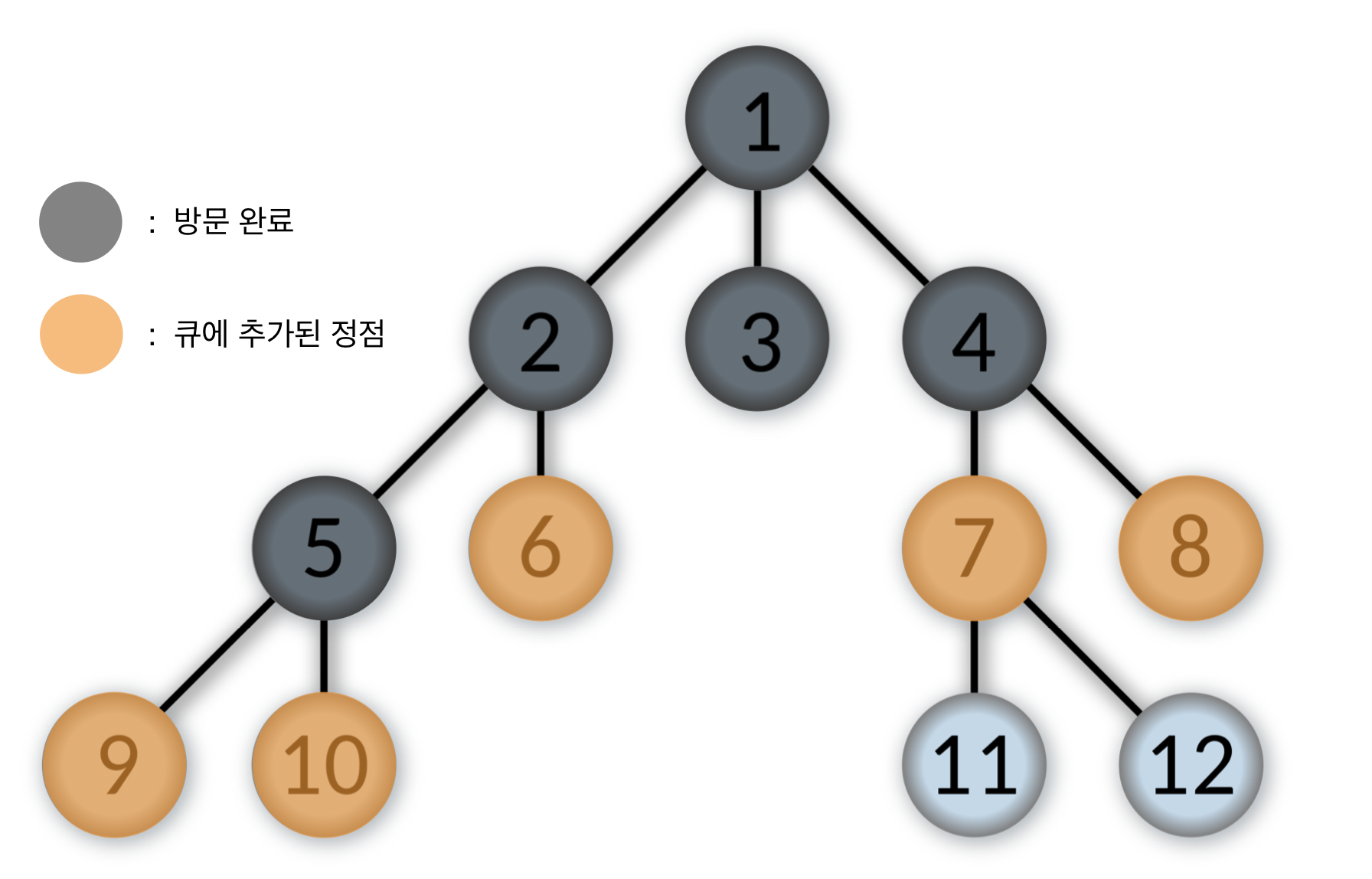
• 큐에서 제일 앞에 있는 6번을 pop하고, 6번 정점을 방문한다.
  6번 정점과 인접한 정점 중에서 방문하지 않은 정점이 없으므로 다음 스탭으로 간다.
  Queue: [7, 8, 9, 10]

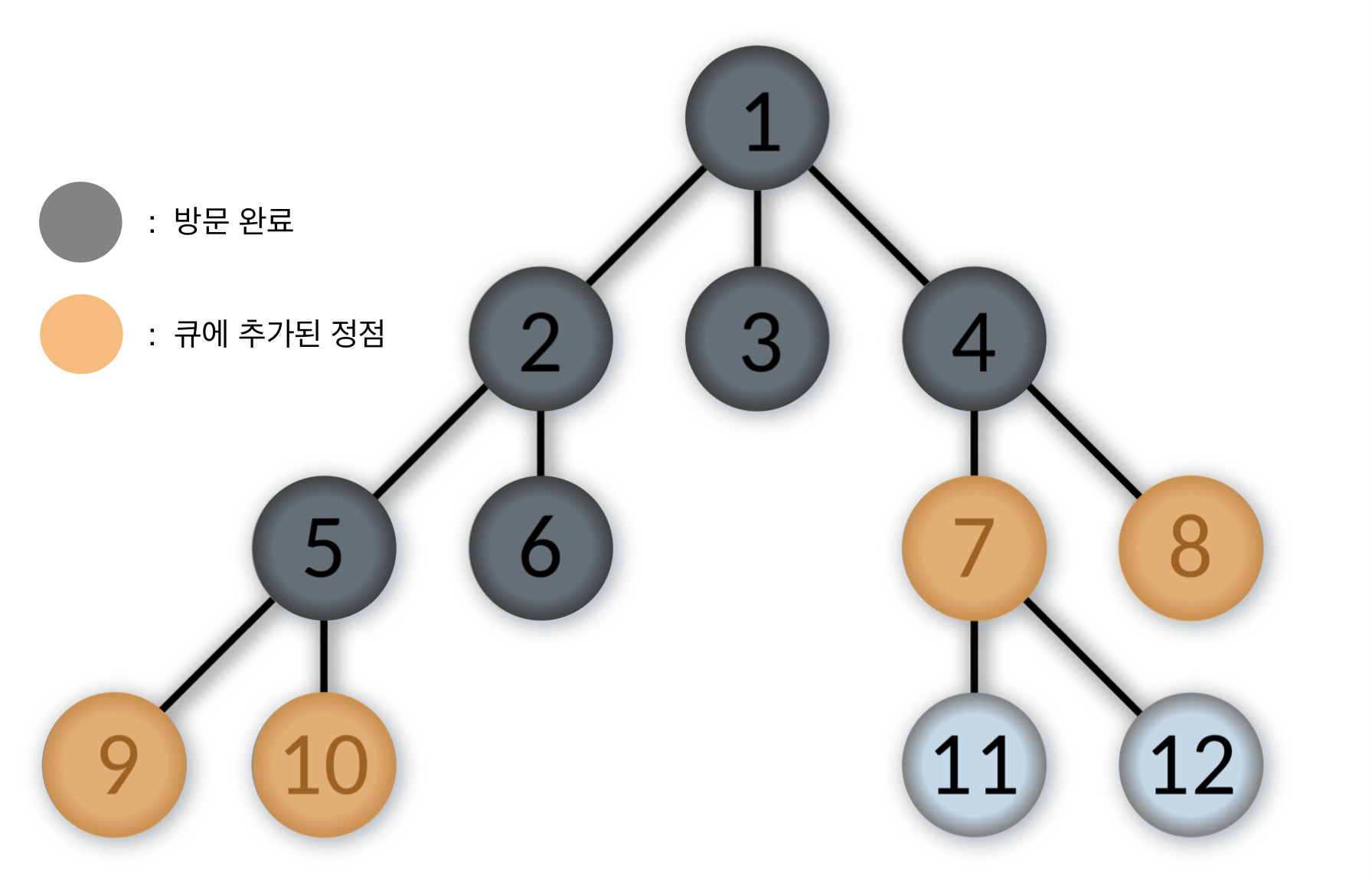
• 큐에서 제일 앞에 있는 7번을 pop하고, 7번 정점을 방문한다.
  7번 정점과 인접한 정점 중에서 방문하지 않은 11, 12번을 순서대로 큐에 넣는다.
  Queue: [8, 9, 10, 11, 12]

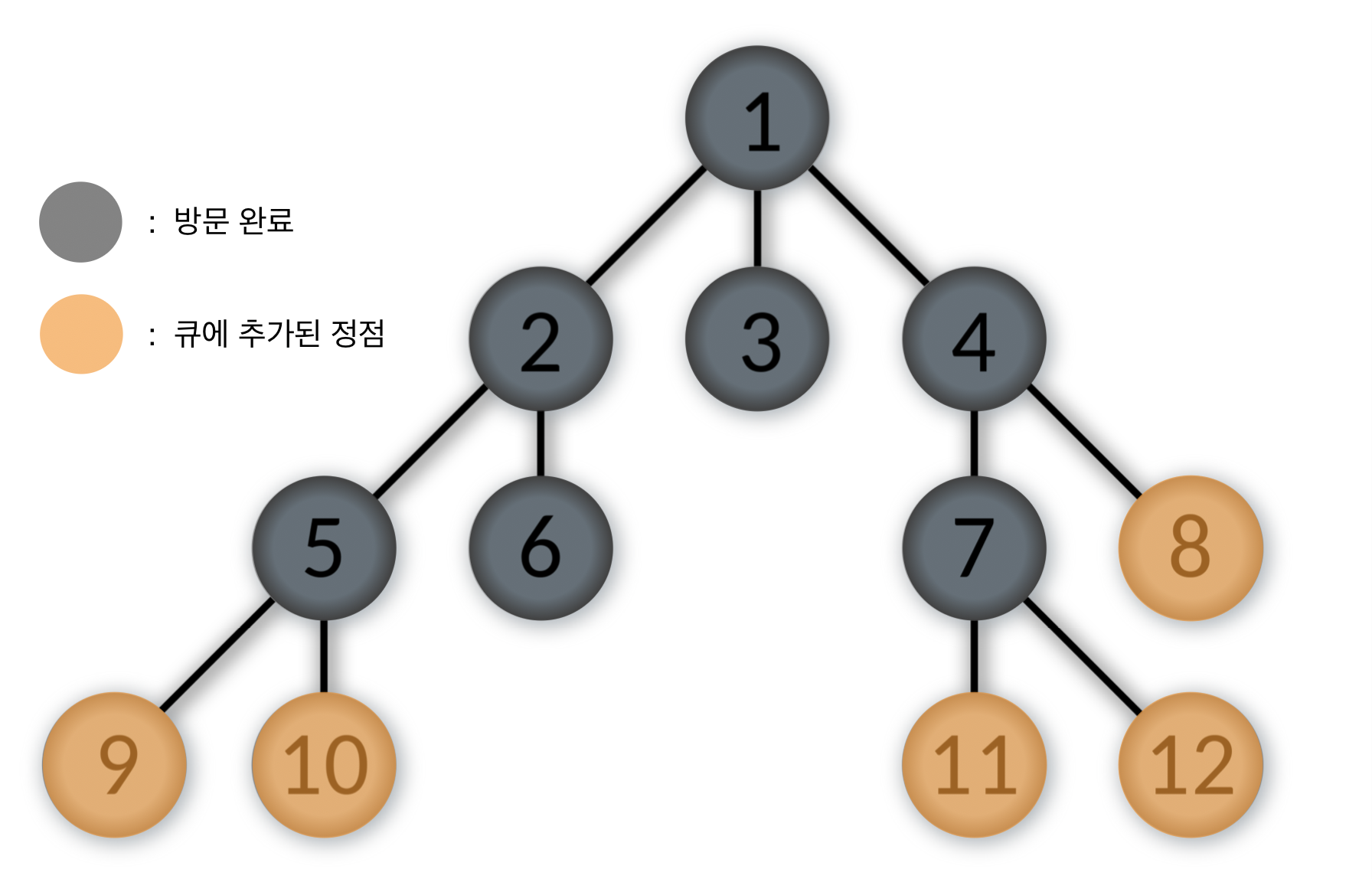
• 큐에서 제일 앞에 있는 8번을 pop하고, 8번 정점을 방문한다.
  8번 정점과 인접한 정점 중에서 방문하지 않은 정점이 없으므로 다음 스탭으로 간다.
  Queue: [9, 10, 11, 12]

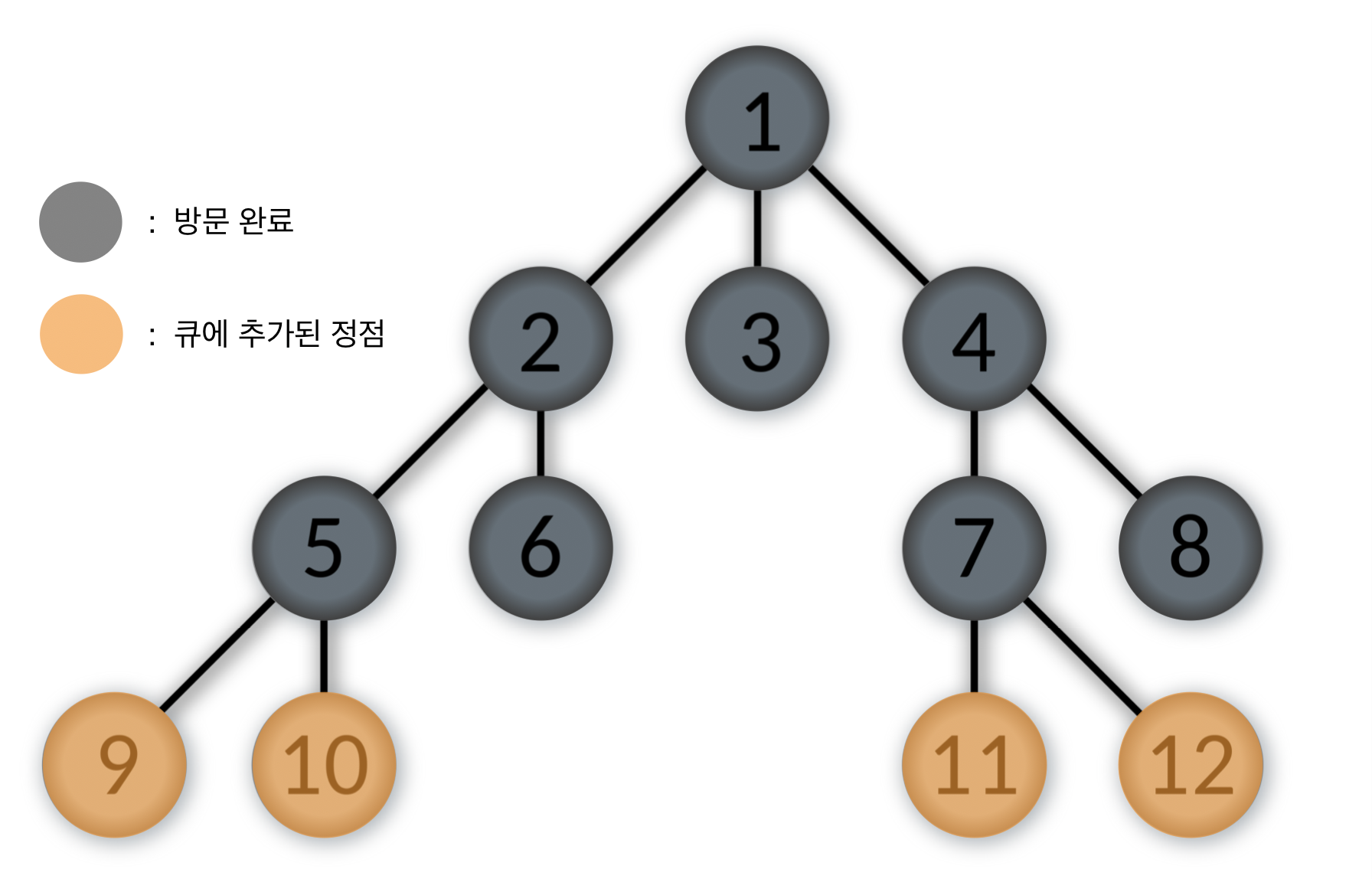
• 큐에서 제일 앞에 있는 9번을 pop하고, 9번 정점을 방문한다.
  9번 정점과 인접한 정점 중에서 방문하지 않은 정점이 없으므로 다음 스탭으로 간다.
  Queue: [10, 11, 12]

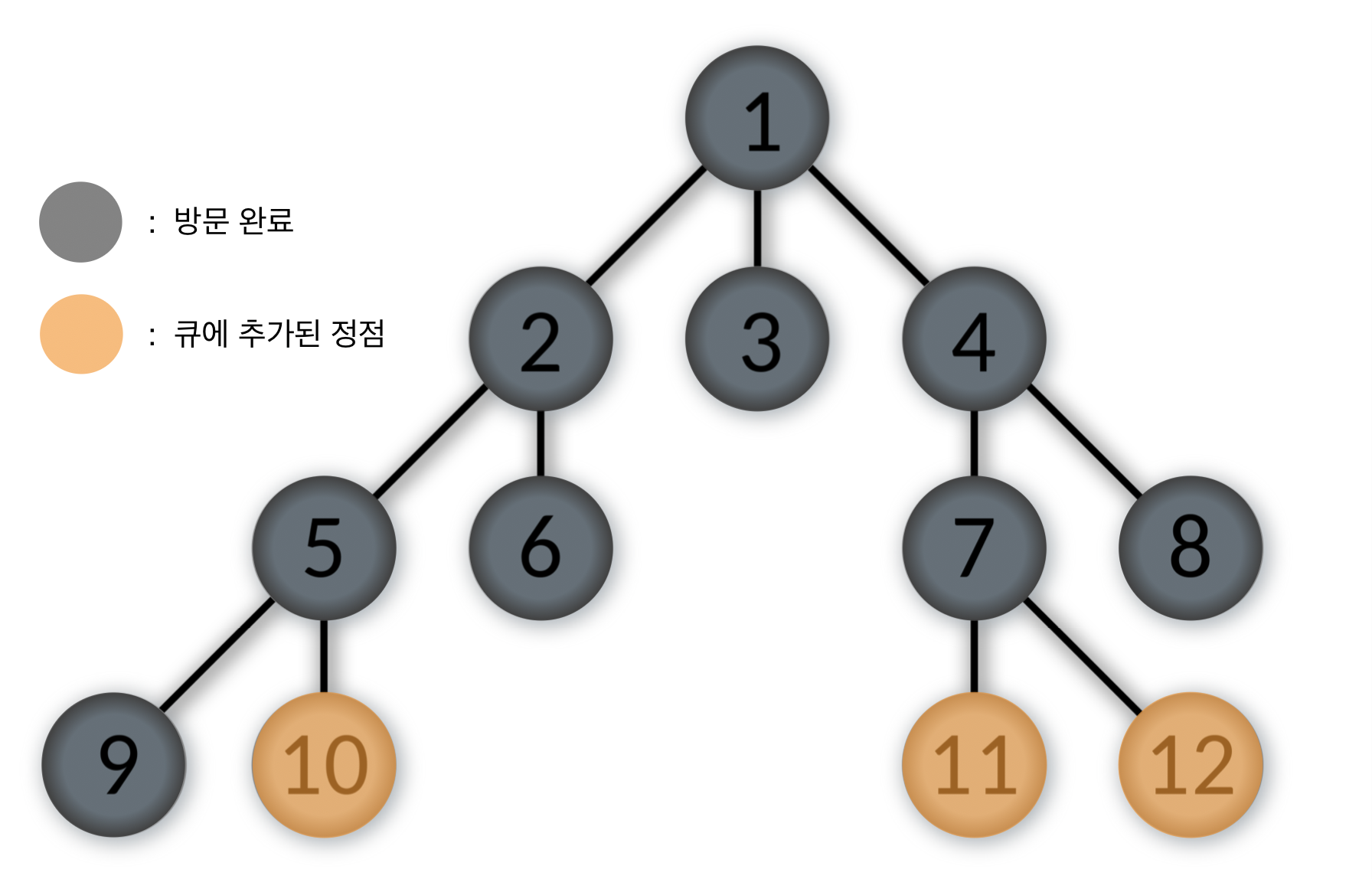
• 큐에서 제일 앞에 있는 10번을 pop하고, 10번 정점을 방문한다.
  10번 정점과 인접한 정점 중에서 방문하지 않은 정점이 없으므로 다음 스탭으로 간다.
  Queue: [11, 12]

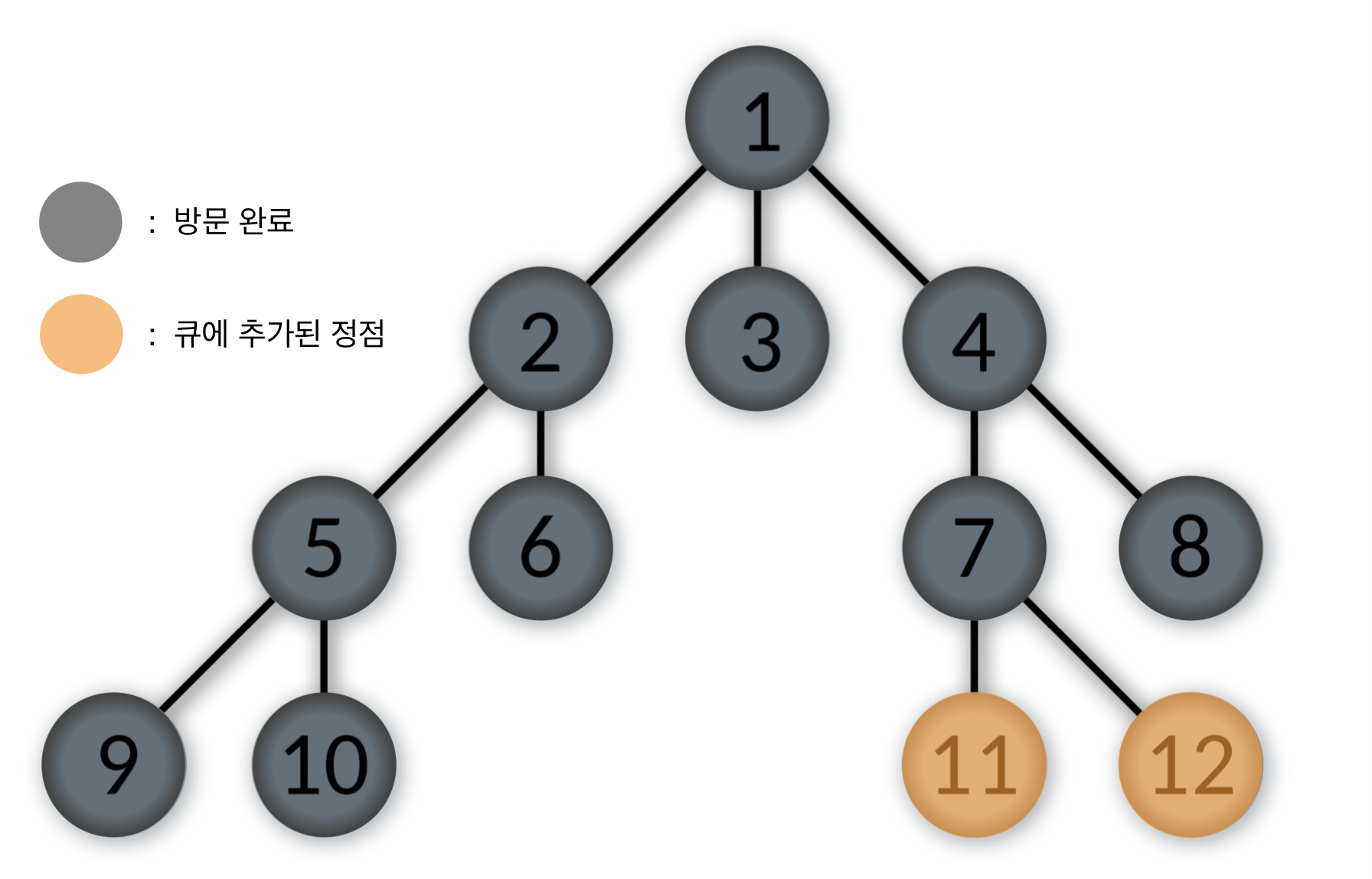
• 큐에서 제일 앞에 있는 11번을 pop하고, 11번 정점을 방문한다.
  11번 정점과 인접한 정점 중에서 방문하지 않은 정점이 없으므로 다음 스탭으로 간다.
  Queue: [12]

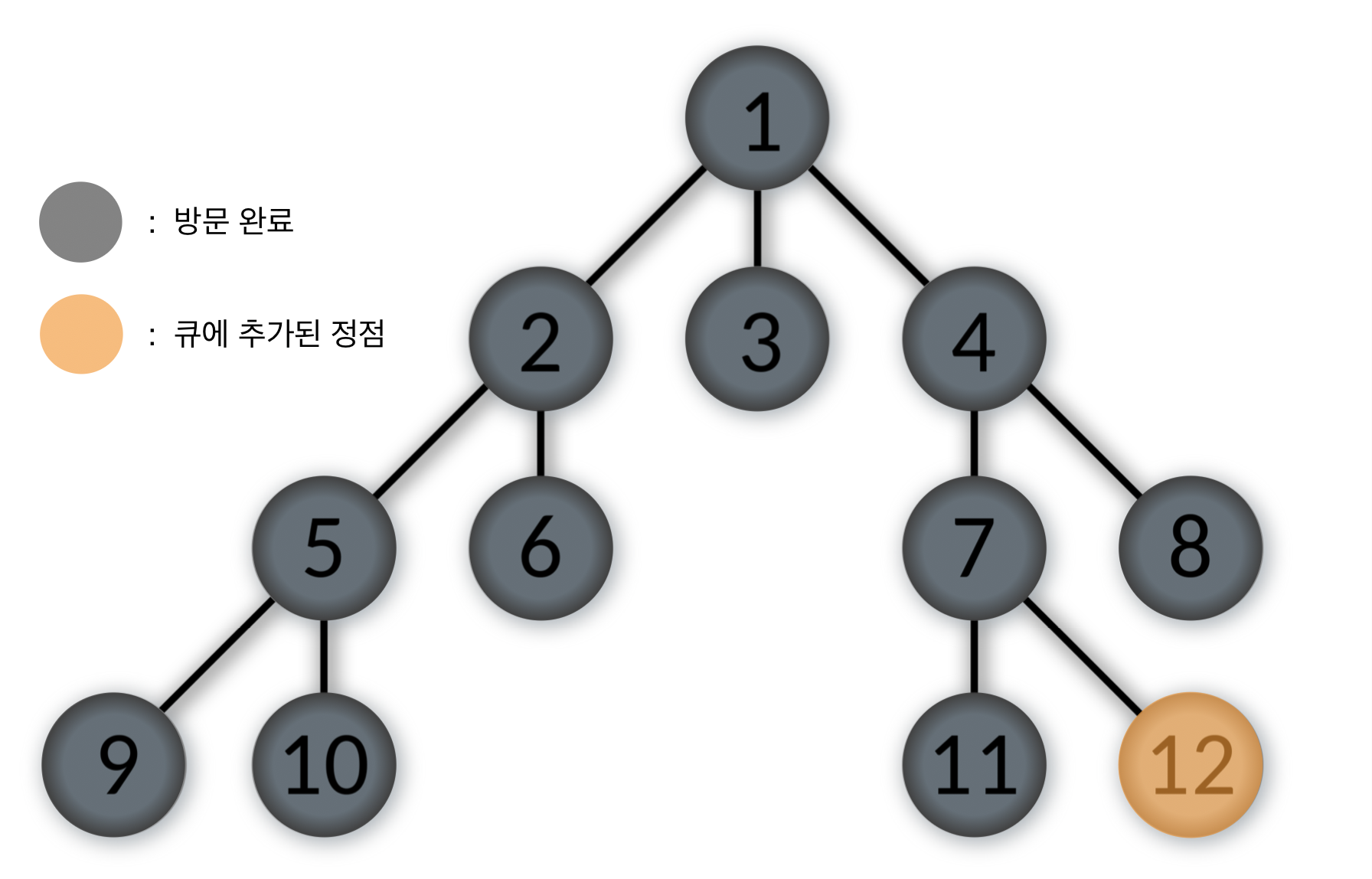
• 큐에서 제일 앞에 있는 12번을 pop하고, 12번 정점을 방문한다.
  12번 정점과 인접한 정점 중에서 방문하지 않은 정점이 없으므로 다음 스탭으로 간다.
  Queue: [ ]

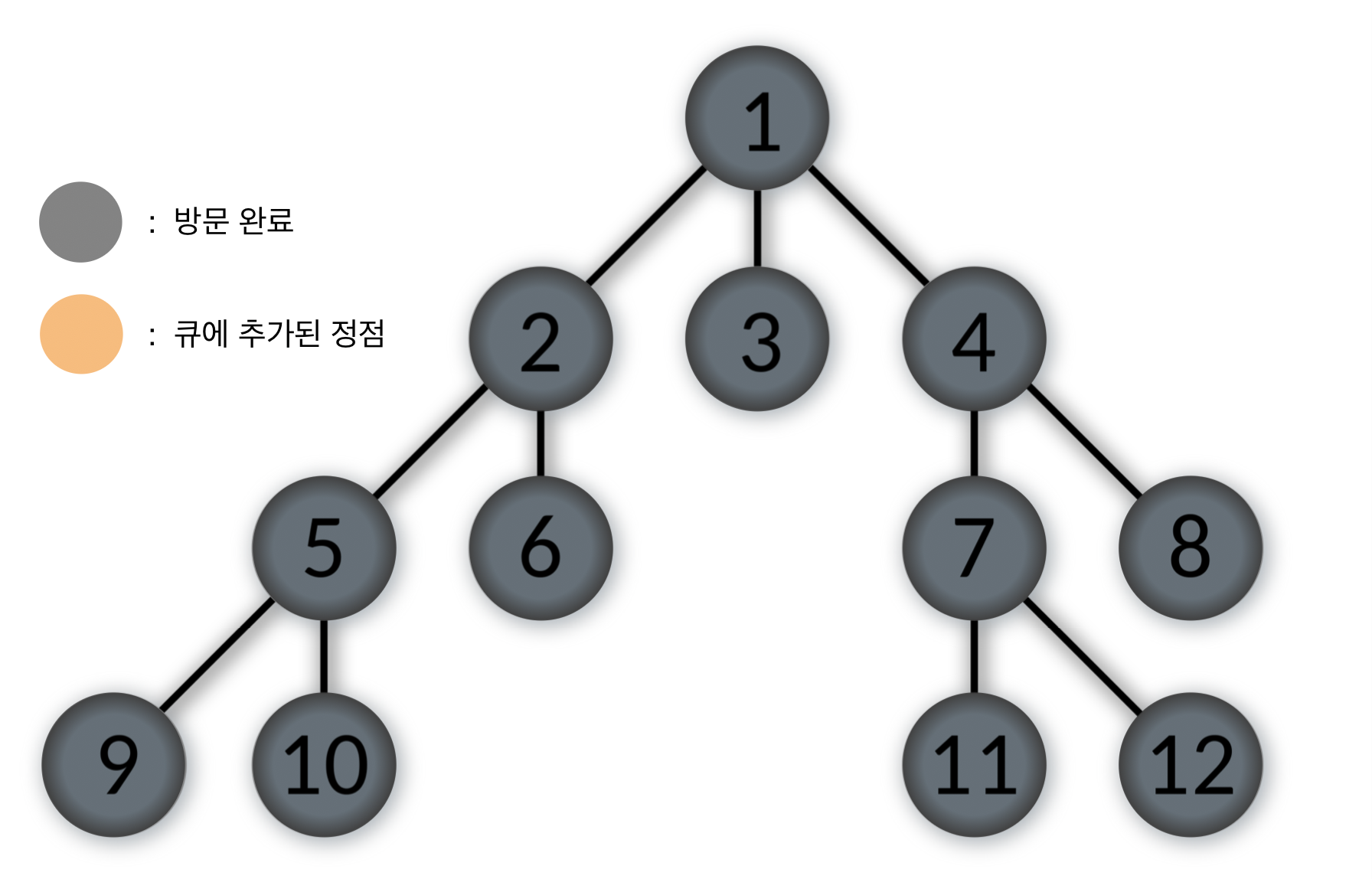
• 큐가 비었으므로 너비우선탐색(BFS)가 완료되었다.

의사코드

Input: 그래프 G, 그래프 G의 시작 루트 정점 v

다음은 Queue를 이용한 BFS의 의사코드이다.

1 procedure BFS(G, start_v) is
2      let Q be a queue
3      label start_v as discovered
4      Q.enqueue(start_v)
5      while Q is not empty do
6          v := Q.dequeue()
7          for all edges from v to w in G.adjacentEdges(v) do
8             if w is not labeled as discovered then
9                 label w as discovered
10                Q.enqueue(w)

한 구문씩 보자.

• let Q be a queue: Queue를 생성한다.

• label start_v as discovered: 시작 루트 정점을 방문표시 한다.

• Q.enqueue(start_v): 시작 루트 정점을 Queue에 넣는다.

• while Q is not empty do: Queue가 빈 공간이 아닐 때 까지 아래를 반복한다.

• v := Q.dequeue(): 현재 방문할 정점 v를 Queue에서 꺼낸다.

• for all edges from v to w in G.adjacentEdges(v) do: v와 인접한 모든 정점 w에 대하여

• if w is not labeled as discovered then: w가 방문표시 되지 않았으면

  • label w as discovered: w를 방문표시 하고

  • Q.enqueue(w): w를 Queue에 넣는다.

위에서 살펴본 예제와 이 의사코드의 한 가지 차이점이 있다면 예제에서는 정점을 큐에서 꺼낼 때 방문표시를 하는 반면, 의사코드 방식에서는 인접 정점들을 큐에 넣을 때 같이 방문표시를 한다는 것이다.

정점의 방문표시를 큐에 꺼낼 때 하거나 큐에 넣을 때 하는것은 어느 구현을 하느냐에 따라 정해진다.

구현

프로그래밍 언어로의 구현은 다음 글을 참고하면 좋다.

• BFS Implementation Using Queue

Applications

너비우선탐색(BFS)은 그래프 이론 분야에서 많은 문제를 해결하는데에 쓰이고 있다.

• 두 정점 u, v간의 최단 경로 찾기 (경로의 길이는 간선의 수에 따라 정해질 때)

• 플로우 네트워크에서 Edmonds–Karp algorithm을 사용하여 최대 유량을 계산 할 때

• 문자열 알고리즘 아호-코라식(Aho-Corasick) 패턴 매칭의 실패 함수(failure function)를 구축할 때

• 그래프에서 정점들이 두개의 독립적인 서로소 그룹으로 나누어질 수 있는가 하는 이분성(bipartiteness) 테스팅

• Copying garbage collection, Cheney’s algorithm

시간복잡도 및 공간복잡도

시간복잡도: $O(|V|+|E|)$ - ($O(|E|)$ may vary between $O(1)$ and $O(|V^2|)$)

너비우선탐색(BFS)의 시간복잡도는 최악의 경우 모든 정점과 간선을 탐색하기 때문에 $O(|V|+|E|)$으로 표현 될 수 있다. $O(|E|)$는 그래프가 얼마나 조밀한가에 따라 $O(1)$와 $O(|V^2|)$사이의 값이 될 수 있다.($|V|$는 정점의 수, $|E|$는 간선의 수이다.)

공간복잡도: $O(|V|)$

그래프의 정점들의 수를 미리 알고 있고, 어떤 정점들이 Queue에 추가되었는지와 같은 정보를 저장하기 위한 추가적인 자료구조를 사용하므로, 공간복잡도는 $O(|V|)$로 표현될 수 있다. 이 공간복잡도는 BFS의 탐색을 위한 공간 요구사항 이므로, 그래프 구축을 위해 사용되는 공간 요구사항과는 별개이다.

References

• Wikipedia
• JavaTpoint