비선형 구조와 탐색
비선형 구조란 i번째 원소를 탐색한 다음 그 원소와 연결된 다른 원소를 탐색하려고 할 때, 여러 개의 원소가 존재하는 탐색구조를 말한다.
일반적으로 자료가 트리나 그래프로 구성되어 있을 경우를 비선형 구조라 하고 이러한 트리나 그래프의 모든 정점을 탐색하는 것을 비선형 탐색이라고 이해하면 된다.
비선형 구조는 선형과 달리 자료가 순차적으로 구성되어 있지 않으므로 단순히 반복문을 이용하여 탐색하기에는 어려움이 있다. 그러므로 비선형구조는 스택이나 큐와 같은 자료구 조를 활용하여 탐색하는 것이 일반적이다.
비선형 구조의 탐색은 크게 깊이우선탐색(depth first search, dfs)과 너비우선탐색 (breadth firth search, bfs)으로 나눌 수 있으며, 이 두 가지 탐색법에 대해서 알아본다.
비선형 구조
비선형 구조의 탐색을 다루기 전에 그래프와 트리에 대해서 간단히 알아보자.
트리와 그래프를 이루는 기본 요소를 정점(vertex)과 간선(edge)이라고 한다.
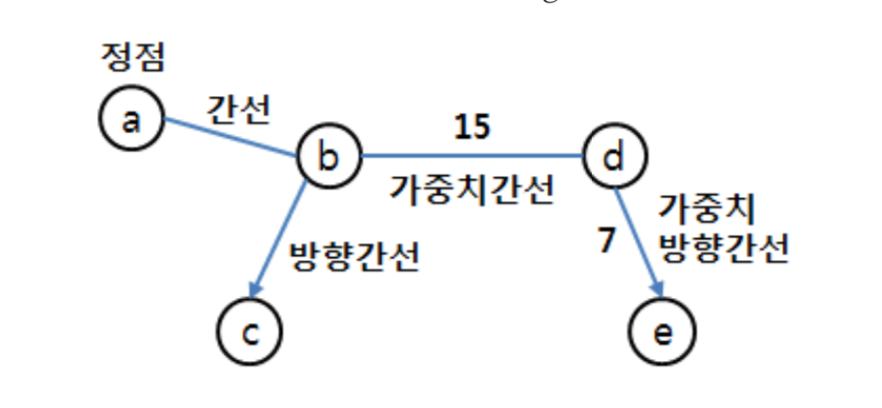
원은 정점, 선분은 간선을 나타내며, a-b는 보통간선, a->b는 방향간선, b-d는 가중치가 15인 양방향통행 간선, d->e는 가중치가 7인 일방통행 간선(방향간선)을 나타낸다.
정점은 점 또는 원으로 표현하며, 일반적으로 상태나 위치를 표현한다. 간선은 정점들을 연결하는 선으로 표현하며, 정점들 간의 관계를 표현한다.
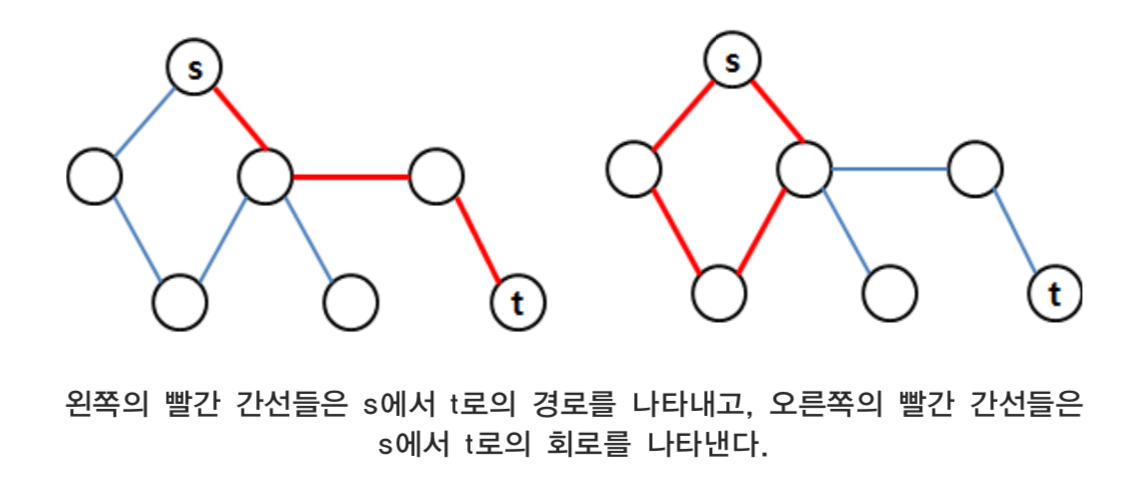
경로(path)와 회로(cycle)
그래프에서 임의의 정점 s에서 임의의 정점 t로 이동할 때, s에서 t로 이동하는데 사용한 정점들을 연결하고 있는 간선들의 순서로 된 집합을 경로라고 한다. 회로는 그래프에서 임 의의 정점 s에서 같은 정점 s로의 경로들을 말한다.
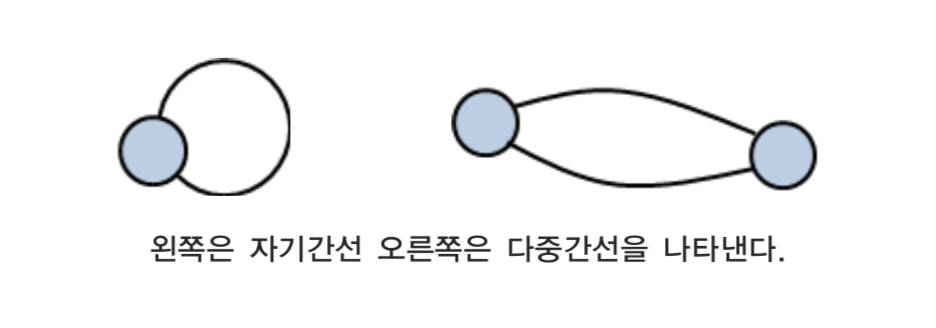
자기간선(loop)과 다중간선(multi edge)
임의의 정점에서 자기 자신으로 연결하고 있는 간선을 자기간선, 임의의 정점에서 다른 정점으로 연결된 간선의 수가 2개 이상일 경우를 다중간선이라고 한다.
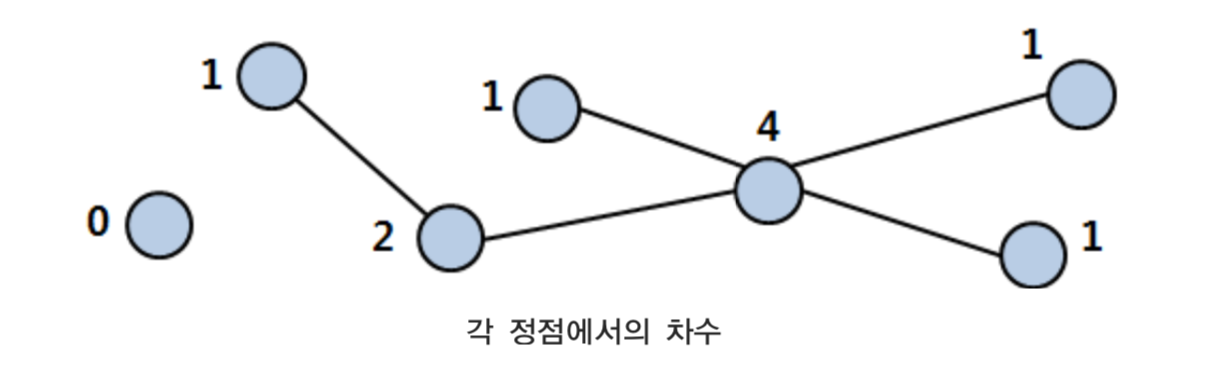
그래프의 차수(degree)
그래프의 임의의 한 정점에서 다른 정점으로 연결된 간선의 수를 차수라고 한다.
그래프의 구현
그래프를 구현하는 방법은 인접행렬(adjacency matrix)과 인접리스트(adjacency list)로 크게 나눌 수 있다.
tip: 프로그래밍 대회에서 그래프는 보통 정점의 수, 간선의 수, 각 간선들이 연결하고 있는 정점 2개로 이루어진 정보가 주어진다.
다음과 같은 그래프가 주어질 때, 이를 표현하는 2가지 방법을 알아본다.
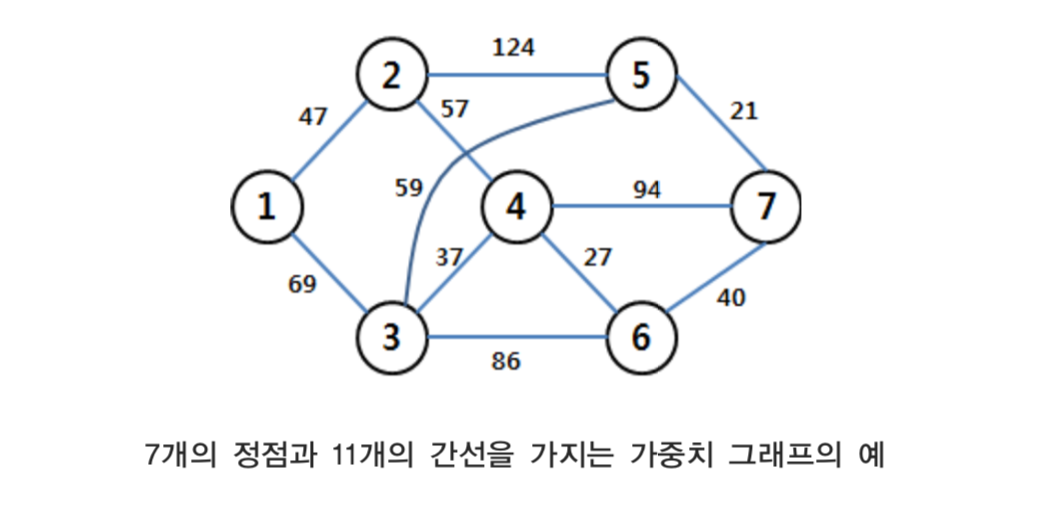
위 그래프의 입력 형식과 입력 데이터의 예
입력 형식:
첫 번째 줄에 정점의 수 n과 간선의 수 m 이 공백으로 구분되어 입력된다.
두 번째 줄부터 m개의 줄에 걸쳐서 간선으로 연결된 두 정점의 번호와 가중치가
공백으로 구분되어 입력된다.
입력 데이터:
7 11
1 2 47
1 3 69
2 4 57
2 5 124
3 4 37
3 5 59
3 6 86
4 6 27
4 7 94
5 7 21
6 7 40
인접행렬의 구현
입력예시를 인접행렬로 받기 위해서는 2차원 배열을 이용한다.
먼저 최대 정점의 수에 맞추어 2차원 배열을 선언하고 각 배열의 칸에 연결된 정보를 저장한다.
앞 그래프를 2차원 행렬을 이용하여 다음과 같이 저장한다.
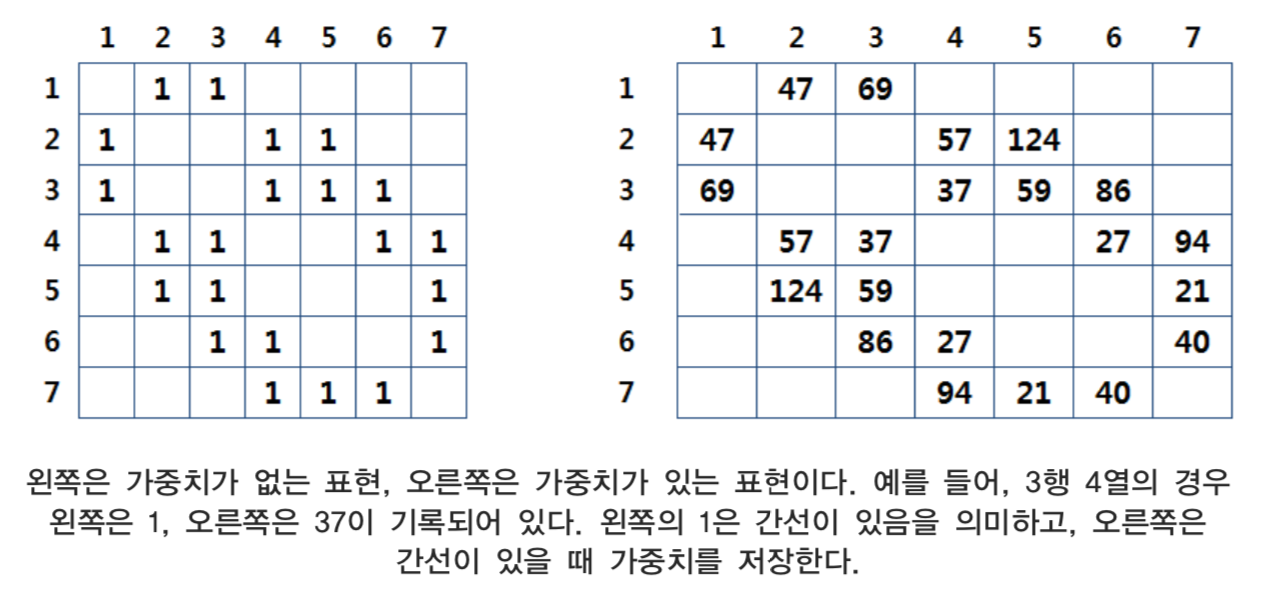
2차원 행렬을 이용하여 저장하는 소스코드는 다음과 같다. 단 최대 정점의 수는 100개 로 가정한다.
C language
#include <stdio.h>
int n, m, G[101][101];
int main() {
scanf("%d %d",&n,&m);
for(int i=0; i<m; i++) {
int a, b, w;
scanf("%d %d %d", &a, &b, &w);
G[a][b]=G[b][a]=w;
}
}
인접리스트의 구현
인접행렬로 표현할 때에는 연결되지 않았던 부분까지 모두 표현이 된다. 즉, 각 칸에 0 이라고 기록된 부분은 연결이 되지 않은 부분을 의미한다. 사실 일반적인 그래프에서 행렬 상에서 0이라고 표현되는 부분이 많을 가능성이 크다.
알고리즘을 구현할 때에도 이 0이라고 표시된 부분까지 모두 조사를 해야 하므로 효율 이 떨어지는 경우가 많다. 이러한 단점을 극복하기 위하여 제안된 방법이 인접리스트이고 이 방법은 인접행렬에서 0으로 표시된 부분은 저장하지 않으므로 효율을 높이고 있다.
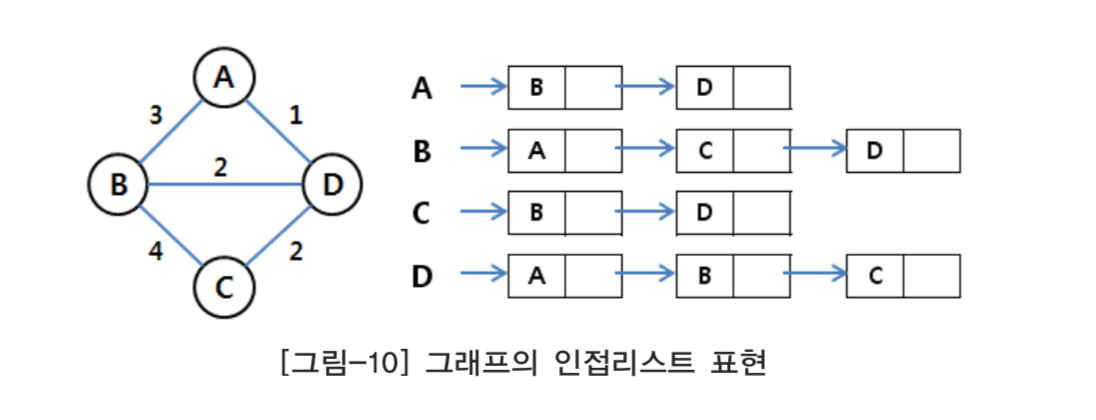
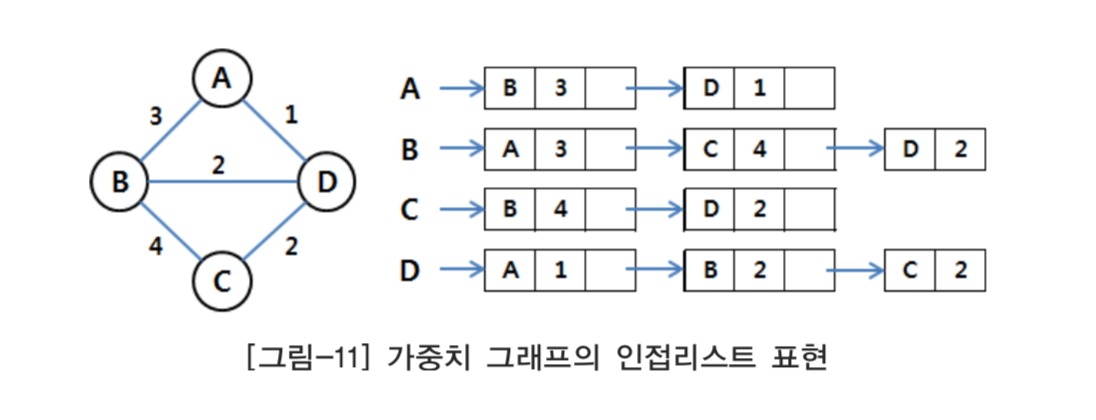
위의 입력 예시를 인접리스트로 구현하기 위해서는 [그림-10], [그림-11]과 같이 연결리스트로 구현할 수 있지만 STL에서 제공하는 C++의 std::vector()를 이용하면 보다 더 간단하게 구현할 수 있다. 위의 입력예시를 인접리스트로 구현하면 다음과 같은 그림이 된다.
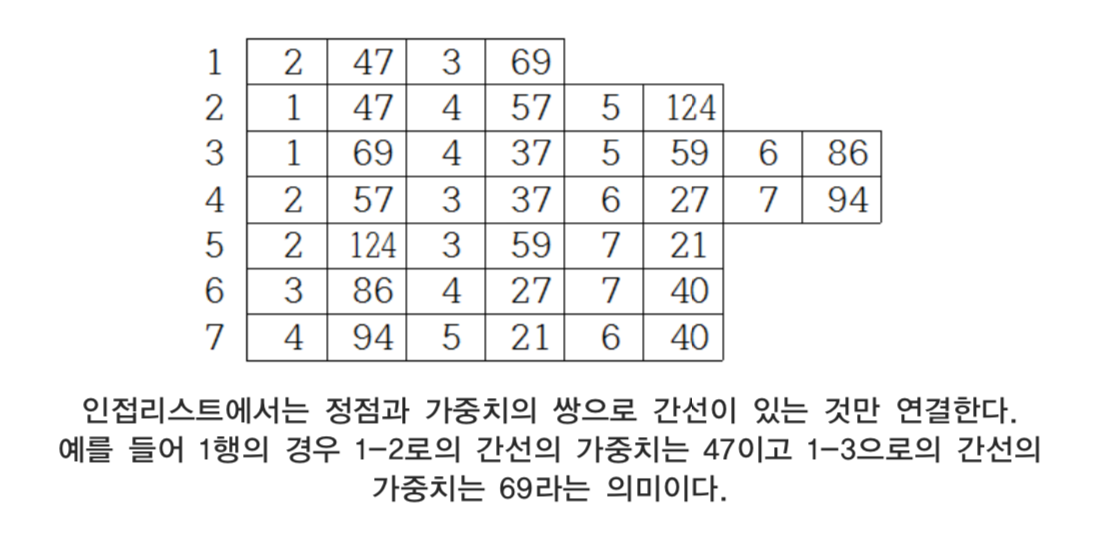
C++의 std::vector()를 이용한다면 위와 같이 인접행렬로 구현하는 것보다 공간을 더 적게 사용한다. 따라서 전체탐색법을 구현할 때, 당연히 탐색시간도 줄일 수 있다. 계산량으로 표현하자면, 인접행렬로 모든 정점을 탐색하는데 O($n^2$)의 시간이 드는데 반해, 인접리스트로 표현하면 O(n+m)의 시간이 든다.
여러 가지 장점으로 인해 인접리스트를 이용한 방법을 활용하는 경우가 많으므로 반드시 익혀둘 수 있도록 하자.
비선형 구조의 탐색
깊이우선탐색(dfs)
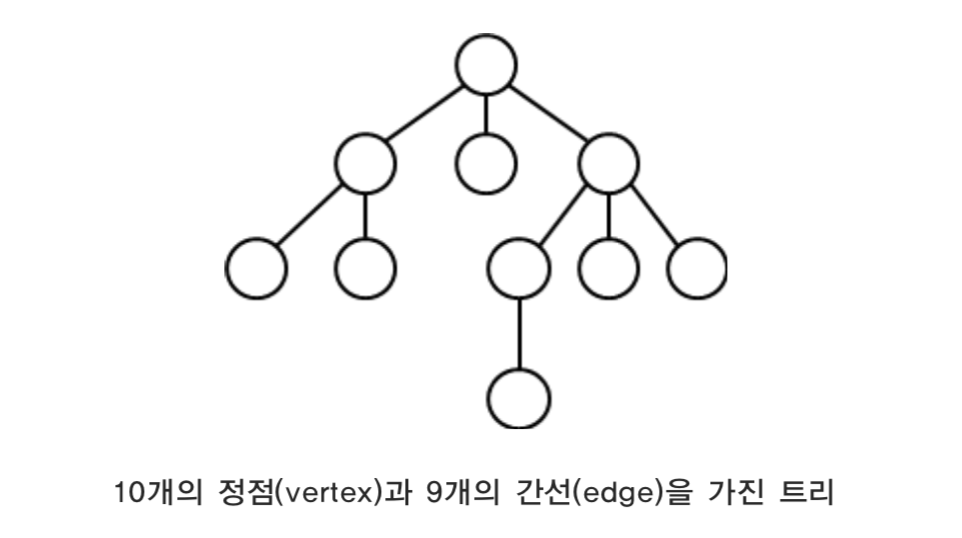
그래프 중 회로(cycle)가 없는 그래프를 트리라고 한다. 다음 그림은 트리를 나타낸다. 이 트리의 가장 위에 있는 정점에서 출발하여 모든 정점들을 깊이우선으로 탐색하며, 탐색 하는 순서를 알아보자.
출발 정점을 트리의 가장 위에 있는 정점으로 하고, 한 정점에서 이동 가능한 정점이 여 러 개 있을 경우 왼쪽의 정점부터 방문한다고 가정하면, 단계별 탐색 과정은 다음과 같다.
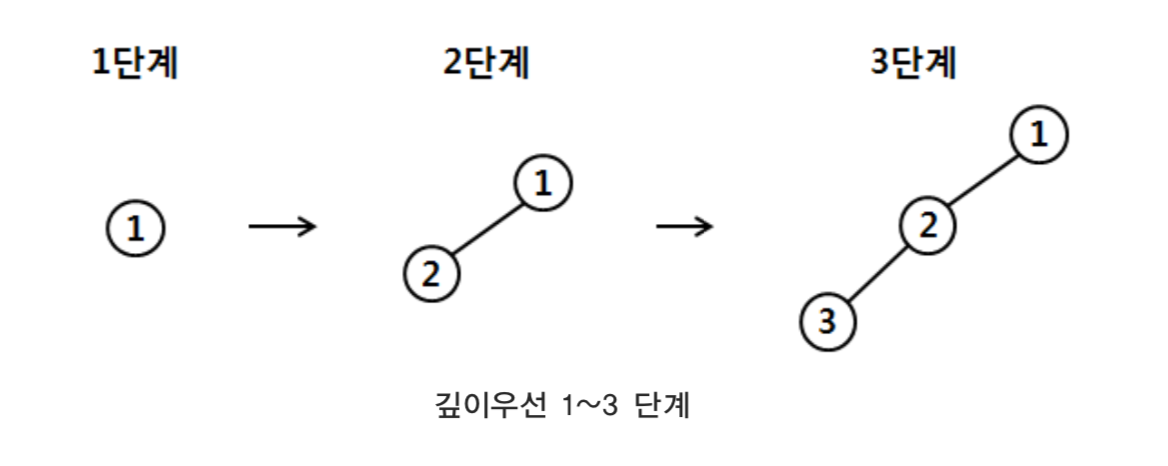
깊이우선탐색과정에서 3단계 이후 더 이상 진행할 수 있는 정점이 없다. 그 이유는 간선 으로 연결된 정점들 중 아직 방문하지 않은 정점을 방문하기 때문이다.
이처럼 더 이상 진행할 수 없을 때는 다시 이전 정점으로 되돌아가는 과정이 필요하다. 일반적으로 이 과정을 백트랙(backtrack)이라고 한다. 백트랙은 비선형 구조의 탐색에서 매 우 중요하다. 백트랙은 스택(stack)이나 재귀함수(recursion)를 이용하면 쉽게 구현할 수 있다.
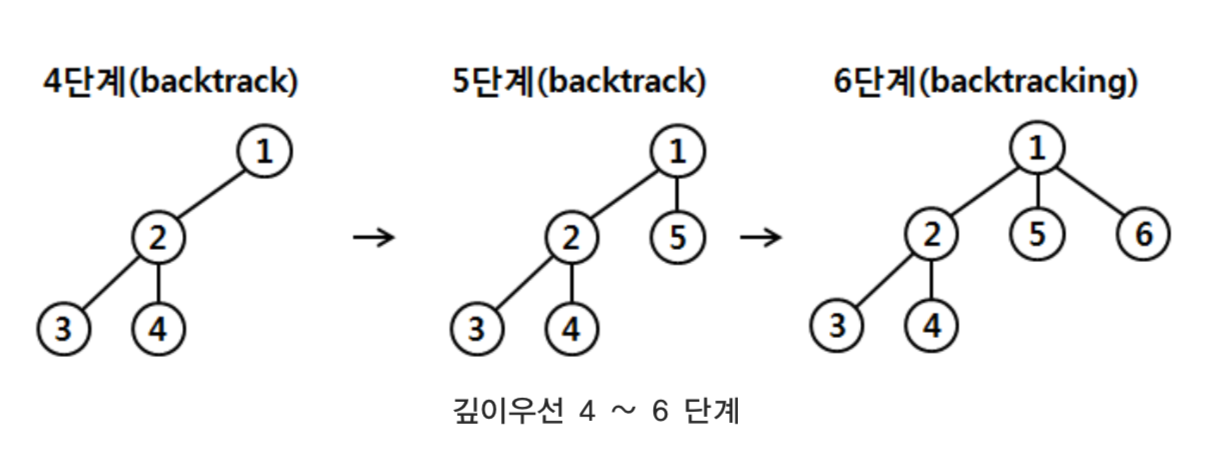
4, 5, 6단계는 연속으로 백트랙이 발생한다. 이는 더 이상 진행할 수 없는 정점까지 도달 했다는 것을 의미한다. 계속 해서 다음 단계로 진행하는 과정은 다음과 같다.
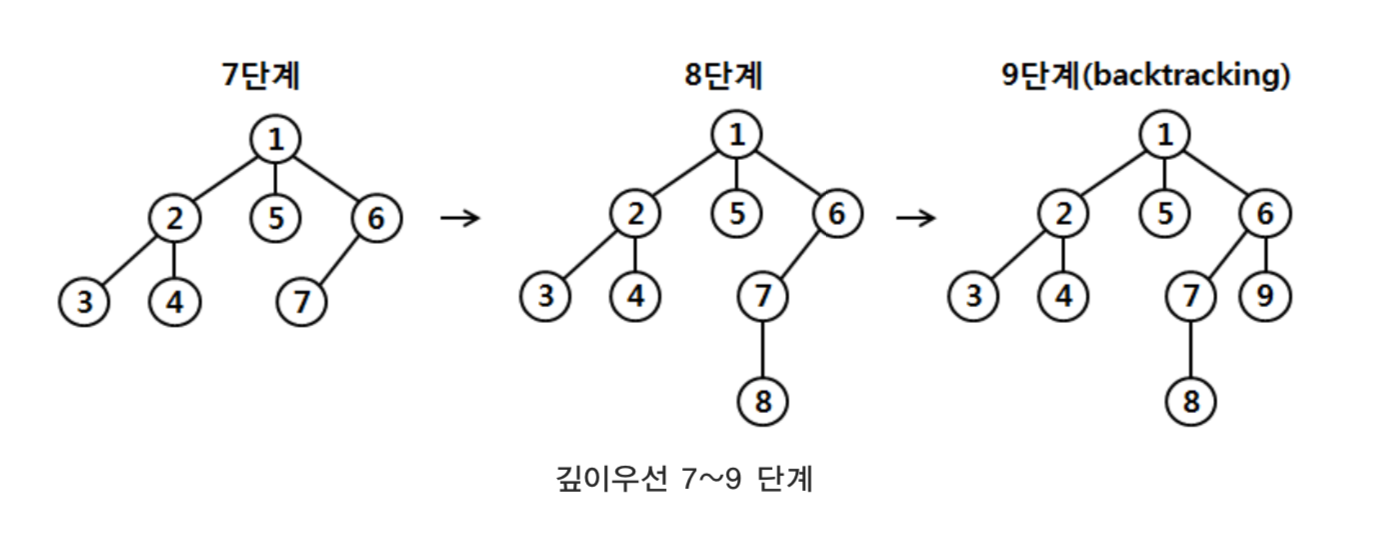
위 단계에서 마지막 정점을 방문하면 깊이우선탐색이 완료된다.
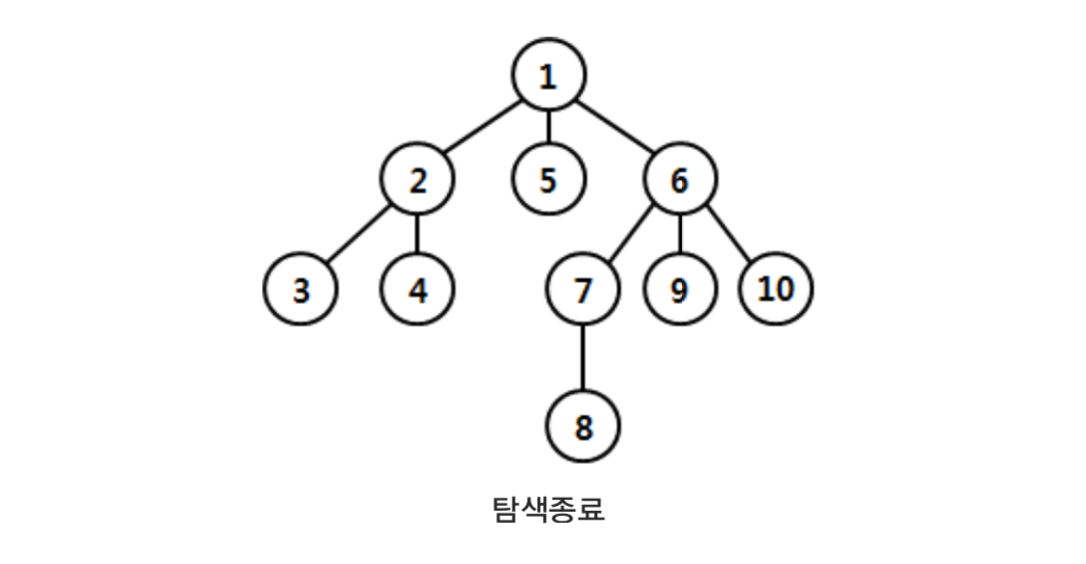
깊이우선탐색을 정리하여 설명하면 먼저 시작 정점에서 간선을 하나 선택하여 진행할 수 있을 때까지 진행하고 더 이상 진행할 수 없다면 백트랙하여 다시 다른 정점으로 진행 하여 더 이상 진행할 정점이 없을 때까지 이 과정을 반복하는 탐색법으로, 간선으로 연결 된 모든 정점을 방문할 수 있는 탐색법이다.
깊이우선탐색의 알고리즘은 다음과 같다. 이 탐색법은 백트래킹(backtracking)이라는 알 고리즘 설계 기법의 중심이 되며 백트래킹 기법은 모든 문제를 해결할 수 있는 가장 기본 적인 방법이므로 꼭 익혀둘 필요가 있다.
깊이우선탐색
bool visited[101]; //방문했는지 체크해 두는 배열
void dfs(int k){
for(int i=0; i<G[i].size(); i++){ // 정점 k와 연결된 모든 정점 방문
if(!visited[G[k][i].to]){ // 만약 아직 방문하지 않았으면
visited[G[k][i].to]=true; // 방문했다고 체크하고
// 깊이우선탐색 진행
dfs(G[k][i]);
}
}
return; //더 이상 갈 길이 없으면 backtrack
}
이 방법은 그래프를 인접리스트에 저장했을 경우에 활용할 수 있다. 전체를 탐색하는데 있어서 반복문의 실행횟수는 모두 m 번이 된다. 일반적으로 인접행렬 보다 속도가 더 빠르기 때문에 자주 활용된다.
너비우선탐색(bfs)
너비우선탐색은 깊이우선탐색과는 달리 현재 정점에서 깊이가 1인 정점을 모두 탐색한 뒤 깊이를 늘려가는 방식이다. 위에서 다룬 ‘10개의 정점과 9개의 간선을 가진 트리’를 통해서 너비우선탐색을 살펴보자.
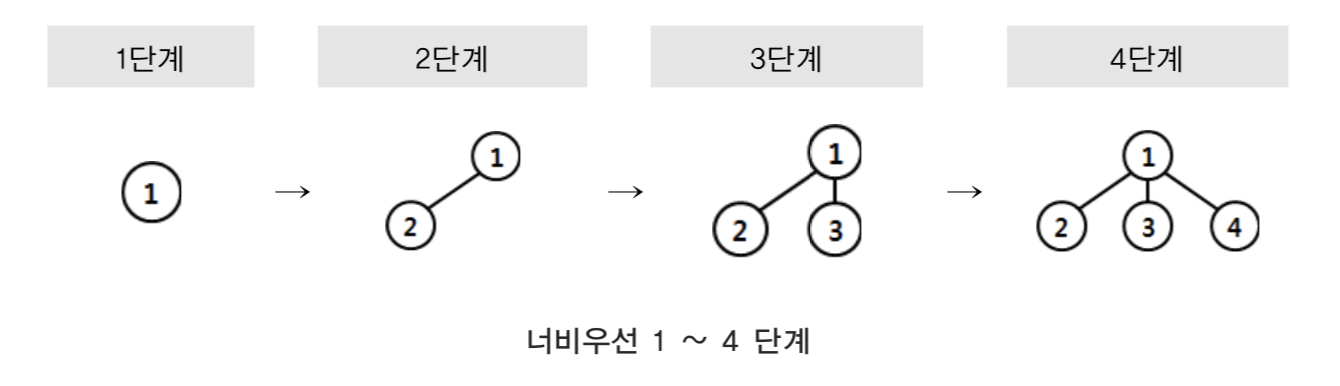
먼저 1단계부터 4단계까지를 살펴보면 1에서 출발하여 깊이가 1인 세 정점을 모 두 순차적으로 방문한다. 계속해서 너비우선탐색의 결과를 살펴보면 다음과 같다.
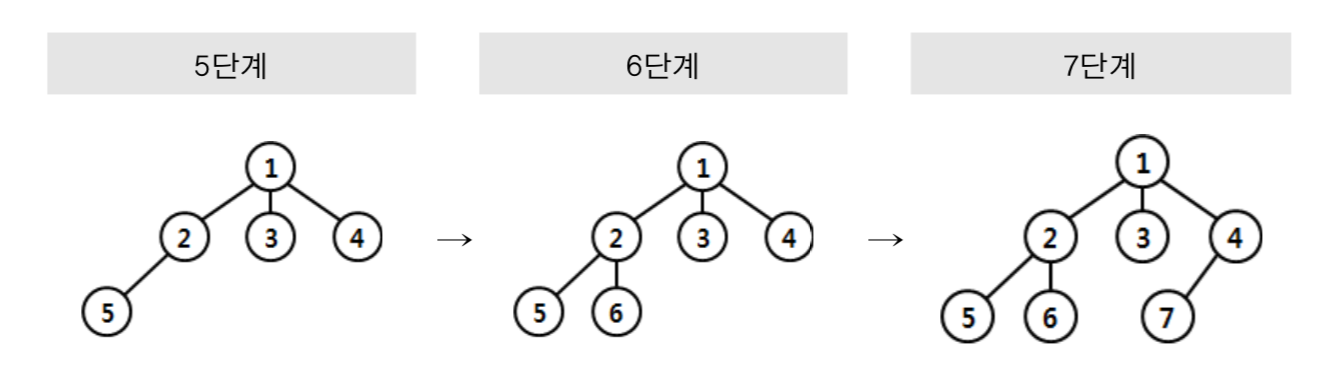
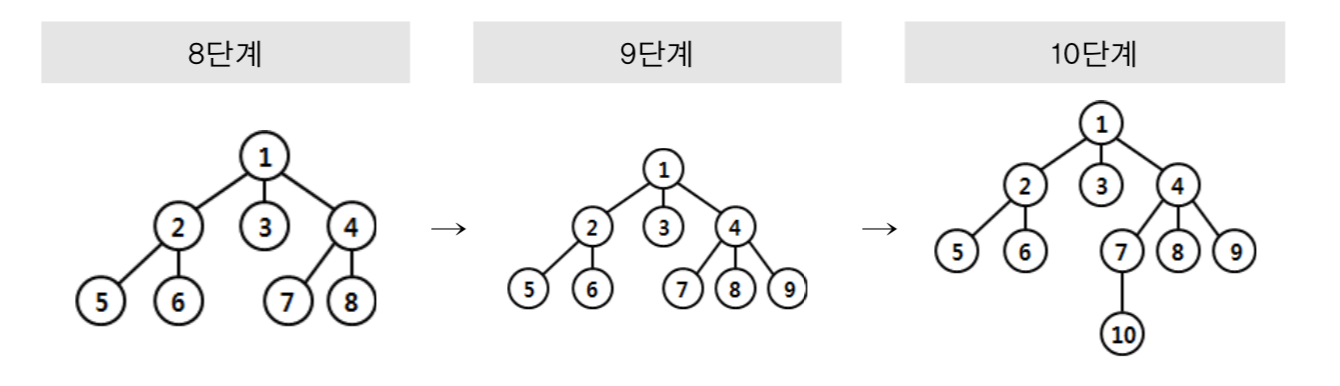
너비우선탐색은 백트랙을 하지 않는다. 대신에 현재 정점에서 깊이가 1인 정점을 모두 방문해야 하므로 큐(queue)라는 선입선출(FIFO) 자료구조를 활용하여 현재 정점에서 깊이가 1 더 깊은 모든 정점을 순차적으로 큐에 저장하여 탐색에 활용한다.
따라서 STL에서 제 공하는 std::queue()를 활용하는 방법을 익힐 필요가 있다.
너비우선탐색 알고리즘은 다음과 같다.
#include <queue>
bool visited[101];
void bfs(int k){
std::queue<int> Q;
Q.push(k), visited[k]=1;
while(!Q.empty()){
int current=Q.front();
Q.pop();
for(int i=0; i<G[current].size(); i++){
if(!visited[G[current][i]]) {
visited[G[current][i]]=1;
Q.push(G[current][i]);
}
}
}
}
이 방법은 그래프를 인접리스트에 저장했을 경우에 활용할 수 있으며, 전체를 탐색하는 데 있어서 반복문의 실행횟수는 모두 m번이 된다. 따라서 일반적으로 속도가 인접행렬 보다 더 빠르기 때문에 자주 활용된다.
References
- 문제해결을 위한 창의적 알고리즘

Leave a comment